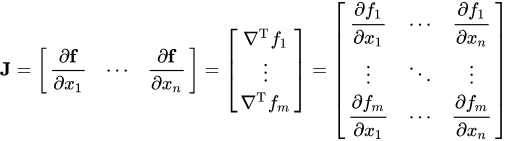StyleGAN2 논문 이해하기

2019년 발표된 StyleGAN2의 논문 Analyzing and Improving the Image Quality of StyleGAN을 읽고 요약, 정리한 글입니다.

0. Abstract

이 논문에서 말하고자 하는 주요 내용은 아래와 같다.

• 저번에 발표한 StyleGAN이 '데이터 기반 비조건부 이미지 모델링' 분야에서 정말 SOTA였는데, 이번에는 그것의 독특한 산출물(Characteristic Artifacts)을 직접 드러내고 분석해 볼게.
• 또, 모델 아키텍처와 훈련 방법에 대한 변경점도 제안할게.
  • 생성자의 Normalization을 재설계하고, 잠재 코드를 이미지로 매핑할 때 좋은 컨디셔닝을 갖도록 Regularization 할 거야.
  • 이때 쓰이는 'Path Length Regularizer'는 성능적인 이득뿐 아니라 생성자가 더 쉽게 인버전(Invert)되도록 하고, 따라서 생성된 이미지를 특정 네트워크에 안정적으로 귀속(Attribute)시킬 수 있어.
  • 또 우린 생성자가 출력 해상도를 얼마나 잘 이용하는지를 시각화하고, 용량(Capacity) 문제를 정의할 거야. 이건 우리가 추가적인 품질 향상을 위해 더 큰 모델을 훈련시키도록 만들었어.
• 결론적으로 우리의 향상된 모델인 StyleGAN2는 또 다시 SOTA를 갱신했어.

📌 생성자를 Invert 한다는 것은?

생성된 이미지에서 원래의 잠재 코드를 복구하는 과정을 뜻한다. 즉, 생성자의 역방향으로 작동하여 생성된 이미지가 어떤 잠재 코드로부터 생성되었는지를 알아낼 수 있다.

1. Introduction

많은 사람들이 저번 StyleGAN이 생성한 이미지에서 독특한 산출물을 찾아냈다. 우린 이에 대한 두 가지 원인을 정의하고 이걸 없애기 위한 아키텍처와 훈련 방법의 변경점을 설명하겠다.

첫 번째로, 우린 생성자가 자신의 구조적 결점을 우회하기 위해 물방울처럼 생긴(Blob-like) 산출물을 만들어낸다는 것을 발견했다. 다음 섹션에서는 생성자에 사용된 Normalization을 재설계하고 이것을 제거해 볼 것이다.

두 번째로, 고해상도에서의 GAN 훈련을 잘 안정화시키는 걸로 유명한 Progressive Growing 기법 면에서도 산출물을 분석하겠다. 또한 우린 Progressive Growing과 같은 목표를 달성할 수 있으면서도 훈련 중 네트워크의 위상(Topology)을 바꾸지 않는 새로운 설계를 제시하겠다. 이 설계는 생성된 이미지의 유효 해상도를 추론할 수 있게 해주며, 이것이 예상보다 낮은 것으로 밝혀짐에 따라 네트워크 용량 증가의 동기가 되기도 했다.

한편, 생성된 이미지의 품질에 대한 지표 중 Precision and Recall(P&R)은 '학습 데이터와 유사한 생성 이미지의 비율'과 '생성 가능한 학습 데이터의 비율'을 각각 정량화함으로써 추가적인 정보를 제공한다. FID와 P&R은 분류 네트워크를 기반으로 하므로 형상보다는 텍스처에 더 집중하는 경향이 있다.

반면, 잠재 공간의 보간 품질을 측정하기 위해 도입된 지각 경로 길이(Perceptual Path Length, PPL)는 형상의 일관성 및 안정성과도 관련이 있다. 우린 이것을 기반으로 합성 네트워크가 더 부드러운 매핑을 통해 품질을 향상하도록 Regularization 하겠다. (= Path Length Regularizer) 이때, 계산 비용을 줄이기 위해 모든 Regularization의 빈도를 줄여도 효과 면에서 괜찮다는 것도 보이겠다.

마지막으로, 잠재 공간 $W$에 대한 이미지의 투영(Projection)이 우리의 새로운 'Path-Length Regularized StyleGAN2'에서 훨씬 낫다는 것도 보이겠다. 이것은 생성된 이미지를 그 소스로 더 쉽게 귀속(Attribute)하도록 해준다.

• StyleGAN2 구현 코드, 훈련 모델 GitHub - https://github.com/NVlabs/stylegan2

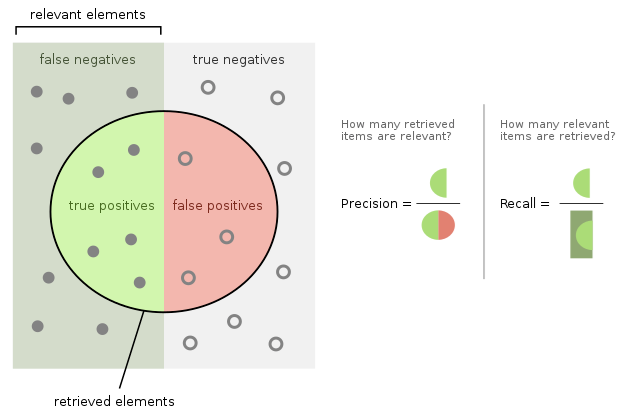
📌 Precision and Recall(정밀도와 재현율)

이진 분류 모델에서 모델의 성능을 평가하기 위한 척도 중 하나이다. (#1) (#2)

• Precision(정밀도): 모델이 True라고 분류한 것 중에서 실제 True인 것의 비율. ($=\frac{TP}{TP + TF}$)
  • GAN에서는 생성된 샘플이 실제 데이터 분포에 얼마나 가까운지를 의미한다. (= 이미지의 품질)
• Recall(재현율): 전체 True인 데이터 중에서 모델이 True라고 분류한 것의 비율. ($=\frac{TP}{TP + FN}$)
  • GAN에서는 생성 모델이 실제 데이터 분포를 얼마나 잘 커버하는지를 의미한다. (= 이미지의 다양성)

2. Removing Normalization Artifacts

우린 StyleGAN이 생성한 이미지에서 특징적인 물방울 무늬가 보인다는 것을 발견했다. 최종 이미지에서는 눈에 띄지 않더라도 중간 계층의 특징 맵에서는 선명하게 보일 수 있다. 이 현상은 64×64 해상도에서부터 보이기 시작해서 높은 해상도로 갈수록 점차 강해진다.

우린 생성자에서 각 특징 맵마다 평균과 분산을 Normalization 하는 AdaIN 연산에 주목했다. Normalization 과정에서 특징 간 상대적인 크기에서 비롯되는 정보가 파괴될 수 있기 때문이다. 우린 이 무늬를 생성자가 의도적으로 Instance Normalization 이후의 신호 강도(Signal Strength) 정보를 몰래 가져온 결과라고 가정했다. (통계를 지배하는 강력하고 국소적인 점을 생성함으로써, 생성자는 다른 곳에서 원하는 대로 신호를 효과적으로 스케일할 수 있다.) 실제로 Normalization 단계를 생성자에서 제거했을 때 이 물방울 무늬도 완전히 사라졌다!

📌 Instance Normalization

각 인스턴스마다 따로따로, 채널별로 Normalize하는 방법이다. 다른 Normalization 방법들과의 비교는 이 게시글을 참고하자.

✅ '통계를 지배하는 점(A strong, localized spike that dominates the statistics)': 이 부분이 조금 해석하기 어려웠는데, 아마도 엄청 진하고 작은 점을 하나 만들어서 이미지 전체의 어떤 통계적 값들을 몰아주고, 대신 다른 곳을 좀 더 쉽게 다루려는 경향이 있었다는 느낌 같다...

실제로 위 그림에서 아랫줄은 생성자가 가끔 물방울 무늬를 만들어내지 못했을 때의 경우인데, 특징 맵의 얼굴 부위 신호가 엄청나게 강해져서 결국 최종 이미지까지 심각하게 손상된 것을 볼 수 있다.

2.1. Generator Architecture Revisited

우린 먼저 기존 StyleGAN 생성자의 몇몇 디테일을 수정하여 새로 설계한 Normalization을 더 잘 이용하도록 할 것이다.

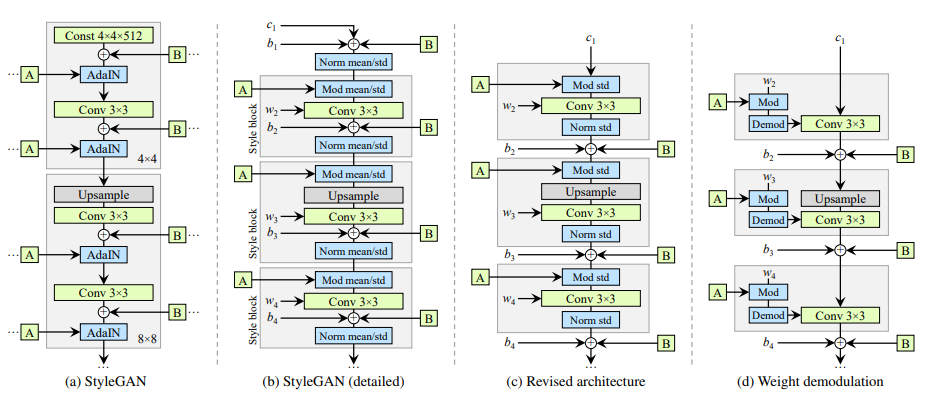
위 그림에서 (a)는 기존 StyleGAN 논문에 제시된 StyleGAN 생성자의 구조이고, (b)는 이것을 좀 더 디테일하게 나눠서 표현한 것이다. (합성곱 계층에서의 가중치 및 편향 표시 & AdaIN 연산을 Normalization과 Modulation으로 분해) 이제 각 회색 박스는 하나의 스타일이 활성화되는 부분을 가리킨다. (= '스타일 블록')

먼저 기존 StyleGAN에서, 스타일 박스 안에서 편향과 노이즈를 적용하면 그 영향력이 현재 스타일의 크기와 반비례하게 된다는 것을 발견했다. 따라서 편향과 노이즈를 스타일 박스 바깥에서 Normalized된 데이터에 적용하도록 했으며 이때 더욱 예측 가능한 결과가 나왔다.

게다가, 이러한 변경 후에 Normalization 및 Modulation이 평균 없이 표준편차만으로도 충분히 잘 작동하는 것을 발견했으며, 상수(Const)에 대한 편향, 노이즈, Normalization도 부작용 없이 제거할 수 있었다. 여기까지가 그림 (c)이다.

✅ 기존 GAN에서 AdaIN 연산을 Normalization과 Modulation으로 쪼갠 후 그 사이에 합성곱 계층이 들어가도록 변경했으며, 이때 오직 표준편차만 사용하여 계산하도록 했다. 또한 편향 및 노이즈 적용 시점을 Normalization 연산 이후로 옮겼고, 상수 입력에 대한 처리 과정을 생략하여 그대로 사용하도록 했다.

2.2. Instance Normalization Revisited

StyleGAN의 주된 장점은 스타일 믹싱(Style Mixing)을 통해 생성된 이미지를 제어할 수 있다는 것이었다. 이때 스타일 Modulation 연산은 특정한 특징 맵을 그 크기에 따라 증폭시킬 수도 있다. 스타일 믹싱이 잘 동작하려면 우린 명시적으로 이러한 증폭을 표본 단위로(Per-sample Basis) 중화시켜야만 한다.

만약 우리가 '스케일별 제어'가 필요하지 않다면 단순히 Normalization을 제거함으로써 FID도 향상시키고 물방울 무늬도 없앨 수 있다. 하지만 이 방법 대신 제어력을 유지하면서도 무늬를 없애는 더 나은 대안을 제시하겠다. 핵심은 '명시적인 강제성이 없는, 특징 맵의 예상 통계량에 대한 Normalization'이다.

(1) Modulation

다시 위 그림 (c)에서, Mod 연산이 합성곱 계층의 입력으로 들어가는 각각의 특징 맵들을 입력되는 스타일에 따라 스케일링한다는 것을 생각해 보자. 이 연산은 합성곱 계층의 가중치를 스케일링하는 것으로도 대체할 수 있다.

• 수식: $w'_{ijk} = s_i * w_{ijk}$ ($s_i$는 $i$번째 입력 특징 맵에 상응하는 스케일 요소, $j$는 출력 특징 맵 인덱스, $k$는 합성곱 연산의 'Spatial Footprint' 인덱스)

(2) Convolution

이제 입력 활성이 i.i.d 난수 값이고 단위 표준편차를 지닌다고 가정(예상)해 보자. 만약 그렇다면, Mod 및 합성곱 연산 이후의 출력 활성은 표준편차 $σ_j = \sqrt{\sum_{i,k}{w'_{ijk}}^2}$를 가진다. 즉, 출력이 상응하는 가중치의 L2 Norm으로 스케일링되는 것이다.

(3) Normalization

기존 Instance Normalization의 목적은 합성곱 계층에서 출력된 특징 맵의 통계에서 $s$의 효과를 본질적으로 지우는 것이었다. 즉 우리는 위의 출력을 다시 단위 표준편차를 갖게끔 복구해야 한다. 이것은 각각의 출력 특징 맵 $j$를 자신의 표준편차의 역수 $1/σ_j$로 스케일링함으로써 달성할 수 있다. (= 'Demodulate' 연산)

이 단계 역시 합성곱 계층의 가중치로 다시 쓸 수 있다('Bake').

• 수식: $w''_{ijk} = w'_{ijk}/\sqrt{\sum_{i,k}{w'_{ijk}}^2 + ε}$ ($ε$는 계산 오류 방지를 위한 매우 작은 값)

위 세 단계를 통해 우린 전체 스타일 블록을 하나의 합성곱 계층으로 Bake 했으며, 그 가중치는 $s$에 따라 조절된다. 이러한 Demodulation 기법은 특징 맵의 실제 내용 대신 '신호의 통계적 추정'에 근거하고 있기 때문에 기존 Instance Normalization보다 약하다. 이것이 위의 그림 (d)이다.

결론적으로, 우리의 새로운 설계는 제어력을 유지하면서도 특징적인 산출물을 제거한다. 지표를 보면 FID는 그리 영향을 받지 않았지만 Precision의 상당수가 Recall로 이동한 것을 볼 수 있는데, 그럼에도 우린 이것이 바람직하다고 본다. Recall은 Truncation을 통해 Precision으로 교환될 수 있기 때문이다.

✅ 2.1.에서 세 부분으로 쪼갰던 연산(Modulation → Convolution → Normalization)을 다시 하나의 합성곱 계층으로 대체했다. 이때 가중치에 쓰인 연산을 Demodulation이라 부르며, 기존 방식보다는 Normalization 효과가 약하지만 이미지에 대한 제어력을 잃지 않으면서 '물방울 무늬'를 성공적으로 제거할 수 있다.

3. Image Quality and Generator Smoothness

FID와 P&R는 생성된 이미지의 품질을 평가하기 위한 좋은 지표이지만, 여전히 잘 못 보는 부분도 있다. 위 그림을 보면 왼쪽보다 오른쪽 사진들이 훨씬 더 진짜 고양이스럽지만, 실제 측정된 FID 및 P&R 값은 매우 유사하다.

한편, 지각 거리 길이(PPL)는 확실히 오른쪽이 더 낮게(즉, 좋게) 측정되었다. PPL은 원래 잠재 공간에서 출력 이미지로 얼마나 부드럽게 보간되는지를 측정하는 방법이었는데, 실제 사람이 인지하는 이미지 품질과도 매우 비슷하게 나타난 것이다.

그 이유로 우린 학습 과정에서 판별자가 '깨진 이미지'에게 패널티를 부여하고, 생성자가 이를 만회하기 위해 좋은 이미지를 만들어내는 잠재 공간의 영역을 늘어나게(Stretch) 한다고 가정했다. 그러나 이는 품질이 나쁜 이미지를 보다 작은 잠재 공간 영역으로 압축시켜(Squeeze) 단기적으로는 평균 품질을 향상시키지만, 점차 왜곡이 누적되면서 훈련 역학(Dynamics)을 손상시키고 최종 이미지 품질까지 나빠지게 만든다.

위와 같은 이유로 PPL을 무조건 작게 만든다고 해서 꼭 이미지 품질이 좋아지는 것은 아니다. 따라서 우린 이러한 단점 없이 생성자의 부드러운 매핑을 목표로 하는 새로운 Regularizer를 소개하겠다. 이때 결과 Regularization 항은 계산 비용이 크기 때문에, 먼저 모든 Regularization 기법에 적용되는 일반적인 최적화 방법을 설명하겠다.

3.1. Lazy Regularization

보통 손실 함수(Loss Function)와 Regularization 항은 하나의 표현식으로 같이 작성되므로 동시에 최적화가 진행된다. 우린 이 Regularization 항을 손실 함수보다 덜 자주 계산하더라도 괜찮다는 것을 알게 되었고, 따라서 엄청난 계산 비용과 메모리 사용을 절약할 수 있었다. 이것이 바로 Lazy Regularization 기법이다.

3.2. Path Length Regularization

우리는 잠재 공간 $W$에서의 고정된 크기의 스텝이 이미지에서의 고정된 크기의 변화를 만들어내길 원한다. (= '잠재 벡터를 조금 변경하면 이미지에도 그만큼의 변화가 생겼으면 좋겠다')

우린 이것에 대한 편차를 경험적으로 측정할 수 있다. 이미지 공간에서 무작위 방향으로 이동하면서 상응하는 잠재 코드 $w$의 그래디언트(변화율)를 관찰함으로써 말이다.

이러한 변화율은 어떤 $w$이든, 이미지 공간에서 어떤 방향으로 이동했든 간에 항상 거의 비슷해야 하며, 이는 잠재 공간에서 이미지 공간으로의 매핑이 'Well-Conditioned'함을 가리킨다.

📌 조건수(Conditional Number)와 'Well-Conditioned'

행렬 $A$와 벡터 $b$에 관한 식 $Ax = b$에서, 조건수(Conditional Number)는 $b$의 작은 변화가 해 $x$에 얼마만큼의 변화를 만드는지를 나타내는 값이며, 조건수가 작을 때 이 식을 'Well-Conditioned'라고 한다. (#1) (#2)

하나의 $w ∈ W$에 대해, 생성자 함수의 매핑 $g(w): W → Y$의 '지역적 메트릭 스케일링 속성(Local Metric Scaling Properties)'은 자코비안 행렬 $J_w = ∂g(w)/∂w$에 의해 표현된다. 벡터의 기대(Expected) 길이를 방향에 상관없이 보존하기 위해, 우리의 Regularizer는 이렇게 정의한다.

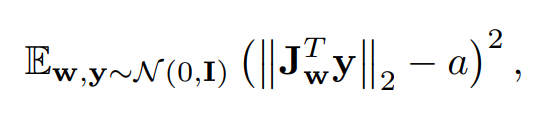
• $y$는 정규 분포에서 뽑은 무작위 이미지, $w$는 $f(z)$를 따르며 $z$는 정규 분포.
• 여기서 자코비안 행렬 $J_w$는 '$w$의 각 방향으로의 변화에 대한 이미지의 각 방향으로의 변화율'을 담고 있으며, $y$가 이미지의 '특정 방향'의 역할을 한다.
• 즉, 둘의 내적 $J_w^Ty$는 '$w$의 각 방향으로의 변화에 대한 $y$의 특정 방향의 변화율'을 뜻하게 된다.

이 식은 모든 $w$에 대해 $J_w$가 직교(Orthogonal)할 때 최소가 된다. 직교 행렬은 길이를 보존하고 차원에 따라 축소(Squeezing)되지 않는다. 이때 자코비안 행렬을 명시적으로 계산하는 대신, $J_w^Ty = ∇(g(w*y))$를 사용하여 역전파를 통해 효과적으로 계산하도록 했다.

상수 $a$는 최적화 과정에서 길이 $||J_w^Ty||_2$에 대한 '장기 지수 이동 평균(Long-Running Exponential Moving Average)'으로써 동적으로 설정되며, 최적화 시 적절한 전역 스케일을 찾아내도록 돕는다.

✅ 위 식이 Regularization 항으로 사용된다면, 모델 학습 시 최적화 과정에서 전체 식의 값을 최소로 만들려 할 것이고, 그 방법은 잠재 코드가 바뀌었을 때의 이미지의 변화량(L2 Norm) $||J_w^Ty||_2$가 특정한 상수 $a$에 항상 가까운 값이 되도록 만드는 것이다.

📌 자코비안 행렬(Jacobian Matrix)

신경망에서 입력에 대한 출력의 그래디언트를 나타내기 위한 행렬로, 각각의 원소들은 1차 미분 계수로 구성되어 있다. 여기서는 잠재 코드 $w$의 각 방향에 대한 이미지의 변화율을 의미하기 위해 사용되었다. (#)

📌 직교 행렬(Orthogonal Matrix)

행렬을 구성하는 모든 벡터의 크기가 1이면서 행벡터들끼리 서로 직교하고 열벡터들끼리 서로 직교하는 행렬이다. 수식 $Q^TQ = QQ^T = I$을 만족한다. (#)

📌 지수 이동 평균(Exponential Moving Average)

전체 데이터 중 일정 부분집합에 대해 연속적으로 이동하면서 평균을 구하되, 최근 데이터일수록 더 큰 가중치를 두어 계산하는 방법이다.

실제로, 우린 이러한 Path Length Regularization이 아키텍처 탐색을 더 쉽게 만듦으로써 신뢰성 있고 일관적으로 행동하는 모델을 이끈다는 것을 발견했다. 적용 결과 PPL 분포가 훨씬 더 좋아졌다. 또한 더 부드러운(Smoother) 생성자는 상당히 쉽게 인버전될 수 있다는 것도 알게 되었다.

4. Progressive Growing Revisited

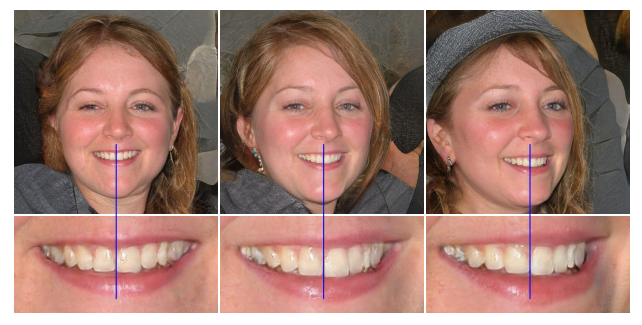
Progressive Growing은 고해상도 이미지 합성 쪽으로 매우 성공적인 기법이지만, 역시 '특징적인 산출물'을 만들어낸다. 주된 문제는 점진적으로 성장하는 생성자가 디테일에 대한 강력한 '위치 선호'를 갖는다는 것이었다. (Phase Artifacts)

• 공개된 영상을 보면 위 이미지에서 머리 각도가 변할 때 치아 부분이 따라 자연스럽게 변하지 않고 계속 멈춰있다가, 어느 순간 갑자기 급격하게 변하는 양상을 보인다.

우린 이 문제의 원인이 Progressive Growing에서 각 해상도가 일시적으로 출력 해상도의 역할을 함으로써 최고 주파수 디테일(Maximal Frequency Details)을 생성하게 되며, 이로 인해 학습된 네트워크의 중간 계층에서 지나치게 높은 주파수가 발생하고 잘못된 이동 불변성(Shift Invariance)을 갖게 되기 때문이라 믿었다.

4.1 Alternative Network Architectures

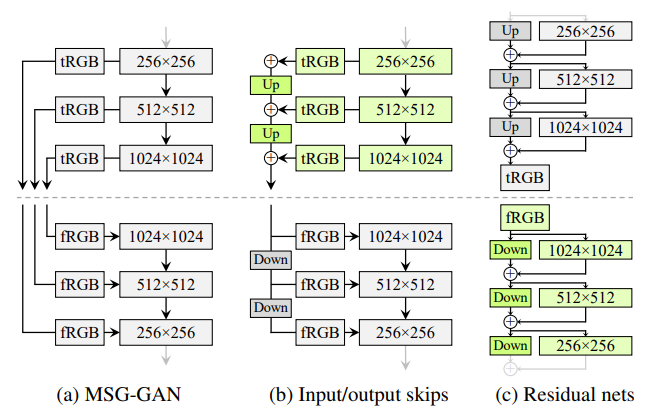
그래서 우린 이러한 Progressive Growing 없이도 고품질의 이미지를 생성해내는 다른 아키텍처들을 알아보았다.

• MSG-GAN: 생성자와 판별자 간 대응되는 해상도끼리 연결하여 'Skip Connection' 구조를 만듦. MSG-GAN의 생성자는 이미지 대신 Mipmap을 출력하며, 실제 각 이미지와 유사한 표현을 계산함.
• Input/Output Skips: MSG-GAN에서 업샘플링과 누적합 연산을 통해 구조를 단순화함. 판별자에서는 반대로 다운샘플링을 수행함.
• Residual Nets: 'Residual Connection'을 사용하여 다시 구조를 변경한 버전.

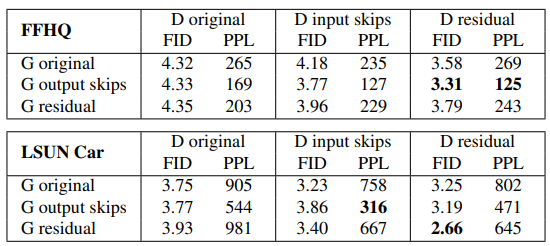
Progressive Growing이 없을 때 기존 StyleGAN과 위 아키텍처들의 성능을 비교한 결과, 모든 모델에서 생성자의 Skip Connection 구조가 PPL을 크게 향상시켰으며, Residual의 판별자가 FID 면에서 확실히 우위를 점했다. (하지만 생성자는 별로였다) 따라서 우린 Progressive Growing 없이 Skip 생성자와 Residual 판별자를 사용해 보도록 하겠다.

✅ Progressive Growing이 일으키는 문제로 인해 이 구조를 쓰지 않으면서도 비슷한 이점을 얻을 수 있는 다른 아키텍처들을 찾아봤으며, 지표 상으로 가장 좋았던 Skip Connections 아키텍처의 생성자와 Residual Net 아키텍처의 판별자를 조합하여 사용하였다.

4.2 Resolution Usage

우리가 유지하고 싶은 Progressiv Growing의 핵심적인 부분은, 처음에는 생성자가 낮은 해상도의 특징에 집중하다가 학습이 진행될수록 점차 세부적인 부분으로 관심을 옮기는 것이다. 위의 아키텍처들은 그것을 가능하게 만들었으며, 특히 이러한 현상은 강제되는 것이 아니라 생성자가 스스로 이득이라고 판단하고 행동하는 결과이다.

실제로 이러한 행동을 분석하기 위해서는, 생성자가 학습 과정에서 특정 해상도에 얼마나 강하게 의존하는지를 정량화할 방법이 필요하다. 예를 들어, Skip 생성자에서는 각 해상도에 상응하는 계층이 최종 이미지에 얼마나 기여하는지에 따라 그 상대적 중요성을 추정할 수 있다.

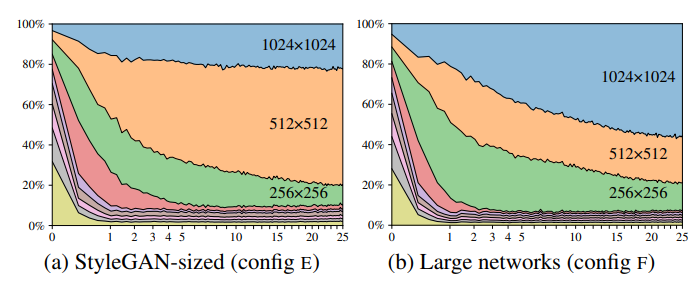
위 표의 (a)는 각 RGB 계층에서 출력된 픽셀 값의 표준편차를 나타낸 것으로, 학습 초기엔 Skip 생성자가 Progressive Growing과 꽤 비슷해 보인다. 하지만 끝으로 갈수록 가장 높은 해상도($1024^2$)를 완전히 활용하지 못하고 있는 것 또한 볼 수 있다. 이때 생성된 실제 이미지를 보면 픽셀 수준의 디테일이 부족해 보이며, 실제 $1024^2$ 해상도의 이미지라기보다는 $512^2$ 이미지를 좀 선명하게 다듬은 것처럼 느껴진다.

이로부터 우리는 네트워크에 용량 문제가 있다고 가정했고, 두 네트워크 모두에서 특징 맵의 숫자를 두 배로 늘려 테스트를 해봤다. 결과는 그림 (b)처럼 고해상도 계층의 기여가 늘어났으며 FID와 Recall 지표도 상당히 향상되었다.

✅ 새로 조합해 사용해 본 구조에서 고해상도 계층을 완전히 활용하지 못하는 문제가 있었는데, 네트워크의 크기를 늘려봤더니 잘 해결되었다. 즉, 새로운 아키텍처가 충분한 용량을 필요로 한다는 것을 알 수 있었다.

5. Projection of Images to Latent Space

합성 네트워크 $g$를 인버전하는 것은 많은 곳에 응용될 수 있다. 주어진 이미지를 잠재 특징 공간 안에서 조작하려면 먼저 알맞은 잠재 코드 $w$를 찾아야 한다. 이전 연구들은 공통적인 하나의 잠재 코드 $w$를 찾는 대신, 생성자의 각 계층마다 별도의 $w$가 선택된다면 결과가 더 좋을 것이라 주장한다. 이렇게 잠재 공간을 확장하는 것은 주어진 이미지에 가까운 코드를 찾겠지만, 동시에 '아무런 잠재 표현이 없어야 하는(즉, 원래 생성자가 생성할 수 없는) 이미지'도 투영(Project)시킬 수 있다.

대신, 우린 잠재 공간을 늘리지 않고 생성자가 생성할 수 있는 원본 이미지에서 잠재 코드를 찾는 것에 집중한다. 우리의 투영 방법은 이전 방법들과 두 가지 면에서 다른데, 첫 번째는 최적화를 진행하는 동안 경사 하강(Ramped-Down) 노이즈를 잠재 코드에 추가한다는 것이다. 이것은 잠재 공간을 더욱 포괄적으로(Comprehensively) 탐사할 수 있게 해준다.

두 번째로 GAN 생성자의 기존 확률론적 노이즈 입력을 추가로 Regularization 한다. 이것은 그들이 똑같은(Coherent) 신호만을 전달하다가 끝나지 않게 하기 위해서이다. Regularization은 '노이즈 맵의 자기 상관 계수(Autocorrelation Coefficients)'를 여러 스케일에 걸쳐 '단위 가우시안 노이즈의 자기 상관 계수'와 일치하도록 만드는 방법을 사용한다.

• 노이즈를 Regularization 하는 자세한 방법은 논문의 부록 D에 나와있으며, 위 그림은 이것을 수행했을 때와 그렇지 않았을 때의 노이즈 맵을 비교한 것이다.
• Regularization을 생략한 경우, 최적화 시 오직 Normalization 연산만 수행하게 되기 때문에 노이즈 맵에 특정 신호가 몰래 가져와지는(Sneak) 것을 볼 수 있다. 즉, Regularization은 이러한 현상을 방지하는 역할을 한다.

5.1. Attribution of Generated Images

조작되거나 생성된 이미지를 진짜와 구별해내는 것은 매우 중요한 일이지만, 이것보단 좀 더 작은 문제를 고려해 보자. 가짜 이미지를 그것의 특정 소스에 귀속(Attribute)시키는 것이다. 이것은 제시된 이미지를 재합성(Re-synthesis)하는 $w$가 존재하는지를 확인하는 것과 같다.

우린 투영이 얼마나 잘 성공하는지를 측정하기 위해 원본 이미지와 재합성된 이미지 간의 LPIPS 거리를 계산했다. 수식으로는 $D_\text{LPIPS}[x, g(\tilde{g}^{-1}(x))]$으로 표현하며, $x$는 분석 중인 이미지, $\tilde{g}^{-1}$는 투영 연산의 근사치를 나타낸다.

StyleGAN2에서 생성된 이미지는 $W$으로 잘 투영되고 따라서 거의 명확히 생성 네트워크에 귀속될 수 있다. 그러나 기존 StyleGAN의 경우, 물론 기술적으로는 상응하는 잠재 코드를 찾을 순 있지만, $W$에서 이미지로의 매핑이 너무 복잡해서 실제로는 안정적으로 성공하지 못한다.

✅ 원본 이미지로부터 상응하는 잠재 코드를 만들어내고(Projection), 그 잠재 코드로부터 다시 이미지를 생성(Re-synthesize)하여 원본 이미지와의 차이를 측정했더니 StyleGAN2가 기존 버전보다 더욱 뛰어났다.

6. Conclusion and Future Work

우린 StyleGAN에 관한 몇 가지 문제들을 확인하고 개선했으며, 품질을 더욱 향상했고 여러 데이터셋에서 SOTA를 갱신했다. 특히 비디오처럼 움직이는 매체에서의 향상이 컸다. 품질 향상과 더불어 StyleGAN2는 생성된 이미지를 소스에 귀속시키는 것도 더 쉽게 만들었다.

학습 성능도 향상되었다. 이러한 속도 향상의 비결은 Weight Demodulation, Lazy Regularization, 코드 최적화에 따른 데이터플로우의 단순화 덕분이다.

향후 Path Length Regularization에 대한 추가적인 개선을 연구하는 것이 유익할 수 있다. GAN의 실용화를 고려하면 학습 데이터 요구량을 줄이는 새로운 방법을 찾는 것도 중요할 것이다. 특히 수만 개의 학습 샘플을 얻는 것이 불가능하다거나, 데이터 자체에 수많은 변종들이 포함된 경우라면 말이다.

---

요약

StyleGAN2는 이전 버전에서 나타난 2가지 문제를 해결하기 위해 만들어진 모델이다.

1. 물방울 무늬 생성 문제 ⇒ Normalization 과정을 포함한 AdaIN 연산이 원인으로, 생성자의 구조를 수정하고 AdaIN 프로세스를 Demodulation 연산으로 변경함으로써 해결하였다.
2. 디테일 위치 선호 문제 ⇒ Progressive Growing 구조가 원인으로, Skip Connections 구조의 생성자와 Residual Net 구조의 판별자를 조합한 새로운 아키텍처를 도입함으로써 해결하였다.

또한 모델의 성능을 향상시키기 위한 다음 내용도 소개되었다.

• 지각 경로 길이(PPL)를 기반으로 만든 Path Length Regularizer를 추가함으로써 잠재 공간과 이미지 공간 사이의 변화가 일관적이게 만들었고, 따라서 두 공간의 매핑이 더욱 부드럽게 정의되도록 했다.
• 생성된 이미지를 원래의 잠재 코드로 더 잘 투영(Projection)시키기 위해 경사 하강 노이즈를 잠재 코드에 추가했고, 기존 확률론적 노이즈 입력에도 Regularization을 수행했다.

📖 도움이 된 자료

• StyleGAN2 공식 영상 - 논문에서 공개한 StyleGAN2의 공식 영상으로, 논문의 핵심적인 내용들을 비디오 형식으로 보여줘서 직관적인 이해에 도움이 되었다.
• 이효석 | [Paper Review] StyleGAN2 - 이번 논문에서 수학적으로 조금 어렵게 느껴지던 부분을 이해하기 쉽게 풀어 설명해주신 글이다.