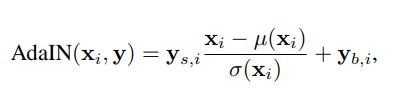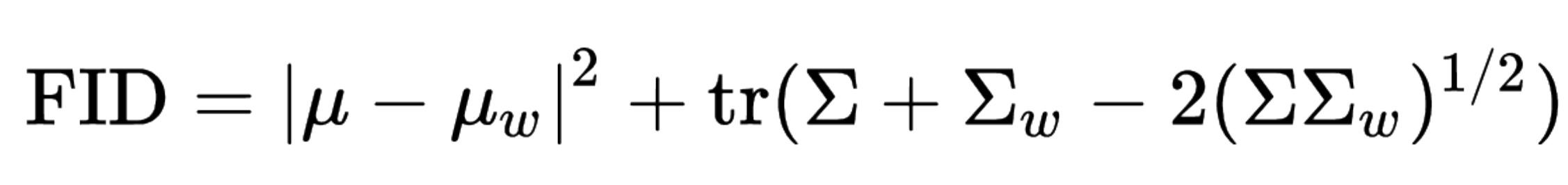StyleGAN 논문 이해하기

2019년 발표된 StyleGAN의 논문 A Style-Based Generator Architecture for Generative Adversarial Networks을 읽고 요약, 정리한 글입니다.

0. Abstract

이 논문에서 말하고자 하는 내용을 요약하면 아래와 같다.

• 우린 스타일 전이(Style Transfer)를 위한 새로운 생성형 적대 신경망(Generative Adversarial Network, GAN)에서의 생성자 아키텍처를 제안할게.
• 이 새로운 아키텍처는 자동으로 학습되고, 고수준의 속성들을 비지도 방식으로 분리할 수 있고, 생성된 이미지에 확률적 다양성(Stochastic Variation)을 부여할 수 있어.
• 이건 전통적인 분포 품질(Distribution Quality) 지표에서 SOTA(State-of-the-Art)이고, 더 나은 보간(Interpolation)과 잠재 요소 간의 분리(Disentanglement)를 가능하게 해. 또한 어떤 생성자 아키텍처에서도 이 둘을 평가할 수 있는 새로운 방법도 제안할게.
• 마지막엔 새롭고 다양한 고품질의 얼굴 이미지 데이터셋도 소개할게.

1. Introduction

GAN에 의해 만들어지는 이미지의 해상도와 품질은 점점 오르고 있지만, 아직 생성자의 이미지 합성 원리를 정확히 이해하기는 어렵다. (Black Boxes) 잠재 공간(Latent Space)의 속성들은 특히 이해하기 힘들고, 서로 다른 생성자들 간 잠재 공간의 보간(Interpolation)을 비교하는 정량적인 방법도 없다.

우린 스타일 전이 연구에 영감을 얻어, '이미지 합성 과정을 제어하는 새로운 방법을 노출하는 식으로' 생성자 아키텍처를 새로 설계했다. 우리의 생성자는 학습된 상수(Learned Constant) 입력을 받아 각 합성곱 계층에서 잠재 코드(Latent Code)를 바탕으로 이미지의 스타일을 조정한다. 즉 직접적으로 이미지가 가진 특징들의 정도(Strength)를 각각의 스케일에 따라 제어할 수 있는 것이다.

이러한 아키텍처의 변화와 더불어 네트워크에 직접 주입되는 노이즈는 생성된 이미지에 있는 고수준의 속성(ex. 자세, 정체성 등 커다란 부분)들을 확률적 변종(Stochastic Variation)(ex. 주근깨, 머리카락 등 무작위하게 변할 수 있는 작은 부분)으로부터 비지도 방식으로, 자동으로 분리할 수 있게 해준다. 또한 직관적인 스케일별 혼합(Scale-Specific Mixing)과 보간 연산도 가능하다. 우린 판별자나 손실 함수에 관해서는 아무 것도 건드리지 않는다.

우리의 생성자는 입력된 잠재 코드를 중간(Intermediate) 잠재 공간에 내장시키는데, 이건 네트워크에서 변동 요소(Factors of Variation)들이 표현되는 방법에 깊은 영향을 준다. 입력 잠재 공간은 반드시 학습 데이터의 확률 밀도를 따르게 되고, 우린 이것이 피할 수 없는 얽힘(Entanglement)을 유발한다고 생각한다. 우리의 중간 잠재 공간은 이러한 제약으로부터 자유로우므로 분리(Disentanglement)될 수 있다. 잠재 공간의 분리 정도를 평가하는 이전의 방법들은 이 경우에 직접 적용될 수 없기 때문에, 우린 새로운 두 가지 지표인 'Perceptual Path Length(지각 경로 길이)'와 'Linear Separability(선형 분리성)'를 제안한다. 이 지표를 통해 기존의 생성자 구조보다 변동 요소끼리 더 선형적이고, 덜 얽힌 표현을 가능하게 한다는 것을 입증하겠다.

마지막으로, 현존하는 고해상도 데이터셋보다 더 높은 품질과 더 넓은 변종을 다루는 얼굴 이미지 데이터셋 FFHQ(Flickr-Faces-HQ)을 제공한다. 이 데이터셋과 우리의 소스 코드, 사전 학습 네트워크는 모두 공개적으로 사용 가능하다.

✅ 지금껏 이해하기 힘들었던 GAN 생성자의 동작 원리를 조금 더 드러내는 새로운 생성자 구조를 설계했다. 서로 복잡하게 얽혀있는 특징들을 분리할 수도 있고, 따라서 각각의 특징을 독립적으로 조절하여 이미지를 변화시키는 것도 가능하다. 얼마나 이 성능이 좋은지 측정하기 위한 지표도 제안하겠다.

2. Style-Based Generator

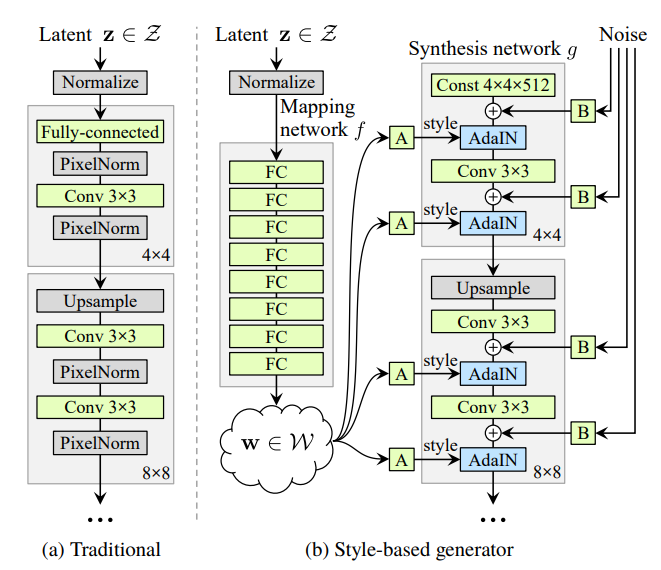
전통적으로, 잠재 코드는 생성자 네트워크 $g$의 첫 레이어의 입력으로 제공됐었다. 우린 여기서 입력 레이어를 아예 생략하고 대신 학습된 상수(Learned Constant)부터 시작한다. 입력 잠재 공간 $Z$의 잠재 코드 $z$에 대해, 비선형 네트워크 $f: Z → W$는 중간 잠재 코드 $w ∈ W$을 만들어 낸다. 이때 단순화를 위해 두 잠재 공간은 512차원으로, $f$는 8개의 레이어를 갖는 MLP으로 두었다. 학습된 아핀 변환(위 그림에서 'A')은 $w$를 스타일 $y=(y_s, y_b)$로 만들며, 이것은 네트워크의 각 합성곱 계층 뒤에 나오는 Adaptive Instance Normalization(AdaIN) 연산을 제어한다.

📌 Adaptive Instance Normalization(AdaIN)

각 특징 맵 $x_i$를 각각 Normalize 한 후, 스타일 $y$의 각 스칼라 요소를 곱하고(Scaled) 더하는(Biased) 연산. 이때 $y$의 차원은 해당 레이어에서 특징 맵의 2배여야 함.

마지막으로, 우린 생성자에게 명시적인 노이즈 입력을 통해 직접적으로 확률적인 디테일을 생성할 수 있는 수단을 제공한다. 이것은 비상관(Uncorrelated) 가우시안 노이즈로 이루어진 싱글 채널 이미지이다. 우린 합성 네트워크의 각 레이어마다 노이즈 이미지를 주며, 노이즈 이미지는 학습된 채널별 스케일링 인자(위 그림에서 'B')를 사용하여 모든 특징 맵에 브로드캐스팅되고, 상응하는 합성곱 계층에 더해진다.

• 합성 네트워크 $g$는 총 18개의 레이어로 구성되며, 2개의 레이어가 짝으로 하나의 해상도를 처리한다.
• 해상도는 $4^2$부터 시작해서 $1024^2$까지 점진적으로 업스케일링된다.

✅ 기존 생성자와 달리 잠재 코드를 바로 입력으로 쓰는 대신, 여러 개의 완전 연결 계층으로 이루어진 매핑 네트워크를 통과시켜 중간 잠재 코드를 얻고, 이걸 다시 아핀 변환을 통해 '스타일'로 만들어준 후 노이즈와 함께 합성 네트워크 전체 레이어에 골고루 더해준다.

2.1 Quaility of Generated Images

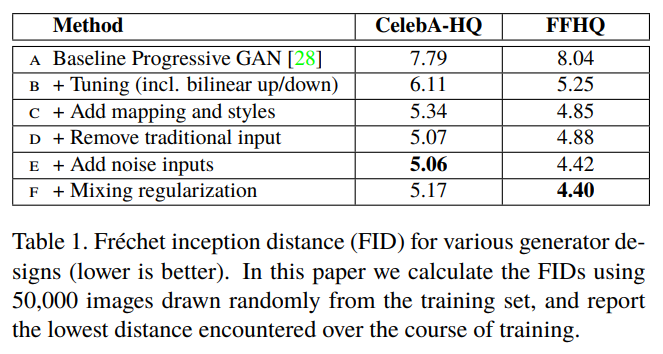
우리 생성자에 대한 특성들을 알아보기 전, 새로운 설계 방식이 이미지의 품질을 오히려 향상시킨다는 것을 증명해 보겠다. 위 표는 가장 기본적인 베이스가 되는 Progressive GAN(PGGAN)부터 특정 기법들을 하나씩 추가하면서 각각의 성능을 매긴 것이다. 성능 평가 지표로는 Fréchet Inception Distance(FID)를 사용했고, 두 가지의 데이터셋(CelebA-HQ와 FFHQ)을 대상으로 했다.

• (B): 쌍선형(Bilinear) 업/다운샘플링을 추가하고, 하이퍼파라미터를 조정하여 더 긴 학습을 수행함.
• (C): 매핑 네트워크와 AdaIN을 추가함. 첫 합성곱 레이어에 굳이 잠재 코드를 주지 않아도 된다는 것을 알게 됨.
• (D): 따라서 기존의 입력 레이어를 제거하고 학습된 상수 텐서를 대신 사용하게 함. 또한 합성 네트워크가 AdaIN 연산을 제어하는 '스타일'을 통한 입력만을 받더라도 충분히 의미 있는 결과를 보인다는 사실도 알게 됨.
• (E): 노이즈 입력을 추가함.
• (F): Mixing Regularization을 추가함.

실험 결과, 스타일 기반 생성자(E)가 기존 생성자(B)에 비해 20% 가까이 FID를 향상시켰으며, 실제 생성된 이미지의 평균적인 품질도 높고, 안경이나 모자 같은 악세사리까지 잘 합성한다는 것을 알 수 있었다.

📌 Fréchet Inception Distance (FID)

생성자에 의해 생성된 이미지의 분포와 실제 이미지의 분포 간 거리를 측정하는 방법이며, 생성된 이미지가 얼마나 진짜 같으면서(Fidelity) 또 얼마나 다양하게 만들어지는지(Diversity)를 모두 평가한다. (#1) (#2) (#3)

• $μ_X$는 벡터 $X$의 평균, $\sum_X$는 벡터 $X$의 공분산 행렬, $\text{tr}$은 대각합(Trace)

FID를 구할 때는 사전 학습된 Inception v3 모델에 실제 이미지와 생성된 이미지를 입력으로 넣어 각각 2,048개의 특징 벡터를 얻어내고, 그 벡터를 이용해 위 식을 계산한다.

참고로 이는 두 다변량 정규분포(Multivariate Normal Distribution) 사이의 거리를 계산하는 방법이며, 단변량일 때는 $\text{FID}=|μ-μ_w|^2+|σ-σ_w|^2$으로 계산할 수 있다.

2.2 Prior Art

지금껏 GAN 구조에 대한 많은 연구는 판별자를 향상시키는 데에만 집중했다. (여러 개의 판별자, 여러 해상도를 다루는 판별자, Self-Attention 등등) 생성자에 대한 대부분의 연구도 주로 입력 잠재 공간의 정확한 분포나 형상에 집중했다. (Gaussian Mixture Model, Clustering, Encouraging Convexity 등등)

최근의 조건부(Conditional) 생성자는 별도의 임베딩 네트워크를 통해 생성자의 많은 계층에 클래스 식별자(Identifier)를 공급한다. 반면, 잠재 코드는 여전히 입력 레이어를 통해 공급된다. 몇몇은 잠재 코드의 일부를 여러 생성자 레이어에 공급하는 걸 고려하기도 했다. AdaINs를 사용하는 'Self Modulate' 생성자는 우리 연구와 비슷하지만 중간 잠재 공간이나 노이즈 입력은 고려하지 않는다.

✅ 대강 이전까지의 연구들과 본인들의 연구의 차이점을 얘기하는 내용이다.

3. Properties of the Style-Based Generator

우리의 생성자 아키텍처는 스케일별로 스타일을 수정함으로써 이미지 합성을 제어할 수 있다. 매핑 네트워크와 아핀 변환을 '학습된 분포로부터 각 스타일에 대한 표본을 추출하는 방법'으로, 합성 네트워크를 '스타일 집합에 따라 새로운 이미지를 생성하는 방법'으로 볼 수 있다. 각 스타일의 효과는 네트워크에서 국소화(Localized)되어 있으므로, 스타일의 특정 부분을 수정하면 이미지의 해당하는 곳에만 영향을 줄 것으로 기대할 수 있다.

이 국소화의 이유를 알기 위해, AdaIN 연산이 먼저 각 채널을 0-평균 및 단위 분산을 갖도록 정규화(Normalize)하고 스타일에 따라 스케일과 편향을 적용한다는 것을 떠올려 보자. 스타일에 의해 구술된 새로운 채널별 통계(Statistic)는 다음 합성곱 연산에서 특징의 상대적 중요성(Relative Importance)을 수정하지만, 정규화 덕분에 원래의 통계량에 의존하지 않는다. 따라서 각 스타일은 다음 AdaIN 연산에 의해 덧씌워지기(Overriden) 전에 오직 하나의 합성곱만을 제어하게 된다.

✅ 각각의 스타일 $y$가 하나의 합성곱 계층에만 영향을 미칠 수 있는 이유는, 매 합성곱 계층마다 AdaIN 연산의 정규화 과정이 선행되기 때문이라는 뜻 같다.

3.1 Style Mixing

스타일을 국소화시키기 위해 우린 Mixing Regularization을 도입했다. 이것은 학습 과정에서 하나가 아닌 두 개의 랜덤한 잠재 코드를 통해 주어진 비율의 이미지를 생성하는 것이다. 이미지를 생성 시 합성 네트워크의 무작위 선택 지점에서, 하나의 잠재 코드에서 다른 잠재 코드로 단순히 전환하는 것인데, 이 연산을 'Style Mixing'이라고 하겠다.

좀 더 자세히 말하자면, 두 개의 잠재 코드 $z_1$, $z_2$를 매핑 네트워크에 넣고, 상응하는 스타일 제어자 $w_1$, $w_2$를 얻는다. 그리고 $w_1$은 교차(Crossover) 지점 전에, $w_2$는 교차 지점 이후에 적용시킨다. 이러한 Regularization 기법은 네트워크가 인접한 스타일이 상관관계가 있다고(Correlated) 추정하는 것을 방지한다.

✅ 학습 과정에서 2개 이상의 잠재 코드를 뽑아 이미지를 생성하는 Mixing Regularization을 거치면 모델의 성능이 더 좋아지며, '교차 지점 앞뒤로 $w_1$, $w_2$를 적용한다'는 것은 생성자 네트워크 $g$의 블록들 중 임의로 중간 지점을 골라 앞의 블록들에는 $w_1$, 뒤의 블록들에는 $w_2$를 각각 따로 적용하여 학습시킨다는 의미이다.

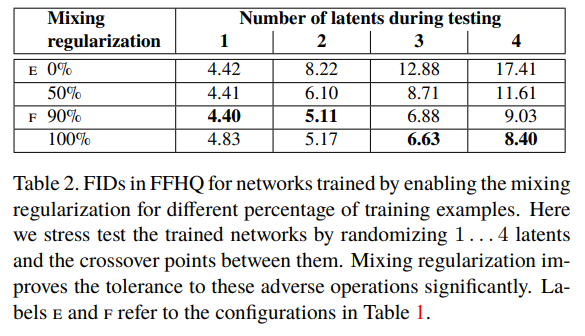
• 위 표는 Style Mixing 시 사용된 잠재 코드의 개수와, 그렇게 만들어낸 이미지를 얼마만큼의 비율로 사용했는지(Mixing Regularization)에 따른 성능 측정값을 나타낸 것이다.

• 위 그림은 소스 B의 특정한 스타일 집합을 복사한 뒤, 나머지 남은 부분을 소스 A로 채워넣어 이미지를 생성한 것이다. (= 두 개의 잠재 코드의 혼합)
  • Coarse한(거친, 큼직한) 해상도의 스타일을 복사했을 때는 자세, 머리 스타일, 얼굴 형태, 안경 등 고수준의 정보를 가져오며,
  • Fine한(고운, 미세한) 해상도의 스타일을 복사할수록 점점 머리카락 색깔이나 피부색 같은 세부적인 수준의 형태를 가져오는 것을 볼 수 있다.

3.2 Stochastic Variation

인물 사진에는 확률적으로 다룰 수 있는 많은 요소가 있다. (머리카락의 정확한 배치라든지, 수염이나 주근깨, 피부 모공 등등) 이것들은 전부 올바른 분포를 따른다는 가정 하에, 이미지에 대한 인지에 영향을 미치지 않고 무작위로 지정될 수 있는 요소이다.

기존의 생성자가 확률적인 변종(Stochastic Variation)을 구현하는 방법을 생각해 보자. 유일한 입력이 네트워크의 입력 레이어를 통해 들어간다는 것을 생각하면, 네트워크는 필요할 때마다 이전의 활성화에서 '공간적으로 다양한(Spatially-Varying) 의사 난수(Pseudorandom)' 값을 생성할 방법이 필요하다. 이건 네트워크의 성능을 소비하고, 또 생성된 신호의 주기성(생성된 이미지에서 반복되는 무늬가 나타나는 등의 현상)을 숨기는 것도 어렵다. 하지만 우린 픽셀별 노이즈를 매 합성곱마다 추가함으로써 이러한 문제를 피할 수 있었다.

• 같은 이미지에 대해 서로 다른 노이즈를 추가했을 때, 이 노이즈가 오직 '확률적인 부분'에만 영향을 주고 다른 전체적인 부분은 그대로 유지시키는 것을 볼 수 있다.
• (c)는 100개의 서로 다른 이미지에 대한 각 픽셀의 표준 편차를 시각화한 것으로, 역시 머리카락처럼 실제로 변하는 부분만 값이 크게 나타나고 있다.

• 위 그림은 노이즈를 생성자의 서로 다른 레이어에 각각 추가했을 때의 결과이다.
• (b)는 노이즈가 없을 때의 결과이고, (a)는 전체 레이어에, (c)는 Fine한 레이어에만, (d)는 Coarse한 레이어에만 노이즈를 추가한 결과이다.
• Fine한 레이어에 노이즈를 추가할수록 머리카락의 곱슬거림이 더 빽빽해지거나 피부 모공이 더 촘촘해지는 등의 변화가 생긴다. 반대로 아예 노이즈가 없을 때는 이러한 디테일이 거의 날아가버린다.

노이즈의 효과는 네트워크에서 완전히 국소화되는 것처럼 보인다. 우린 생성자의 어느 지점에서나 '새로운 내용물을 최대한 빨리 도입해야 한다'는 일종의 압력이 있으며, 네트워크가 가장 쉽게 확률적 변화를 만들어내는 방법은 제공된 노이즈에 의존하는 것이라 가정한다. 새롭게 주어지는 노이즈 셋들은 모든 레이어에서 사용할 수 있으므로, 이전 활성화에서 확률적 효과를 만들 만한 이유가 없고, 따라서 국소적인 효과로 이어지게 된다.

✅ StyleGAN은 이미지에 무작위성을 추가하기 위해 매 계층마다 난수를 생성해 사용하는 대신, 처음부터 무작위 노이즈를 전체 네트워크 계층에 골고루 나눠줬다. 그래서 각 계층이 굳이 이전 계층에 의존하지 않고도 자기가 받은 노이즈만으로(즉, 국소적으로) 확률적 효과를 만들어 내도록 학습할 수 있다는 뜻 같다.

3.3 Separation of Global Effect from Stochasticity

스타일의 변경은 전역적인 효과를 만들고, 노이즈는 오직 관련된 확률적 변동에만 영향을 준다. 이러한 관찰은 기존의 스타일 전이 연구와 일맥상통하는데, 해당 연구에서는 그람 행렬이나 채널별 평균과 같은 공간적 불변 통계량(Spatially Invariant Statistics)은 이미지의 스타일을 잘 인코딩하고, 공간적으로 변동되는 특징들(Spatially Varying Features)은 특정 개체(Instance)를 인코딩한다는 사실이 확립되어 있다.

우리의 스타일 기반 생성자에서는 스타일이 전체 이미지에 영향을 준다. 전체 특징 맵이 같은 값으로 Scaled & Biased 되기 때문이다. 따라서 자세, 조명, 배경과 같은 전역적인 효과는 일관성 있게 제어된다. 한편, 노이즈는 각 픽셀에 독립적으로 추가되며 이건 확률적인 변화를 제어하기에 딱이다. 만약 네트워크가 노이즈로 자세 같은 부분을 제어하려 한다면 공간적인 불일치(Inconsistency)가 발생할 것이고, 따라서 판별자에 의해 페널티를 부여받을 것이다. 즉 네트워크는 명확한 지도 없이도 전역 및 국소적 채널을 적절히 쓰는 법을 익힌다.

✅ 요약하면, 중간 잠재 코드로부터 만들어진 스타일은 이미지의 전체적인 부분을, 노이즈는 무작위성이 존재하는 디테일한 부분들을 맡는다. 이 모든 것들이 스스로 알아서 학습된다!

4. Disentanglement Studies

Disentanglement의 목적은 '선형적인' 하위 공간들로 이루어진 잠재 공간을 만드는 것이며, 이때 각 공간은 오직 하나의 변동만을 제어하게 된다. 그러나, $Z$에 있는 각 요소 간 조합의 표본 확률은 학습 데이터의 해당 밀도와 일치해야 한다. 이것은 요소들이 일반적인 데이터셋 및 입력 잠재 공간과 완전히 분리되는 것을 방해한다.

✅ 예를 들면, '수염 여부'라는 특징과 '성별'이라는 특징을 조합한 결과(수염 있는 남성/수염 없는 남성/수염 있는 여성/수염 없는 여성)의 분포가 실제 학습 데이터의 분포와 일치해야 한다는 뜻 같다. 이게 지켜지지 않으면 이미지를 생성했을 때 '수염 있는 여성'이 나오는 일이 생길 수도 있으니까...

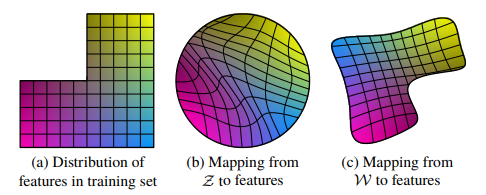
• (a)는 원본 학습 데이터의 특징 간 분포를 표현한 것이다. 가로축과 세로축을 각각 특징 1, 특징 2라고 할 때, 실제로는 특정한 특징 1과 특징 2 값의 조합을 갖는 데이터가 없을 수도 있다. (좌상단 빈 공간, 수염 있는 여자)
• (b)는 $Z$에서 이미지 특징으로의 매핑을 강제로 곡선화하여 금지되었던 조합을 $Z$에서 사라지게 한다. 이건 잘못된 조합을 샘플링하는 일을 예방한다.
• (c)는 $Z$에서 $W$로의 '학습된 매핑'으로, (b)에서의 많은 뒤틀림을 복구(Undo)할 수 있다.

우리 생성자의 주요 장점은 중간 잠재 공간 $W$가 어떤 고정된 분포에 따른 샘플링을 지원하지 않아도 된다는 것이다. 여기서 샘플링 밀도는 학습된 조각별 연속 매핑(Learned Piecewise Continuous Mapping) $f(z)$에 의해 유도된다. 이 매핑은 휘어진 $W$를 곧게 펴서(Unwarp) 변동 요소들을 보다 선형적으로 만들 수 있다. 이처럼 얽힌(Entangled) 표현이 아닌 풀린(Disentangled) 표현에 기반하여 생성자는 더 현실적인 이미지를 쉽게 생성할 수 있다.

✅ $Z$를 바로 사용하지 않고 중간 잠재 공간 $W$로 한 번 매핑 네트워크를 거친 후 사용하면 이미지의 각 특징을 보다 선형적으로 얻을 수 있게 된다는 뜻 같다.

4.1 Perceptual Path Length

잠재 공간 벡터들의 보간(Interpolation)은 이미지에 놀라운 비선형적 변화를 만들어낼 수 있다. 선형 보간 시 양 끝에 없던 특징이 중간 지점에서 나타날 수도 있는데, 이것은 잠재 공간이 얽혀있으며 변동 요인들이 적절히 분리되지 않았음을 뜻한다. 이 효과를 정량화하기 위해, 잠재 공간에서 보간을 수행했을 때 이미지에 '얼마나 과감한 변화가 생겼는지'를 측정해 볼 수 있다. 직관적으로, 덜 휘어진 잠재 공간이 그렇지 않은 공간보다 더욱 부드럽고 덜 급격한 보간을 해낼 것이다.

우리의 측정 기준으로는 '지각-기반 쌍별 이미지 거리(Perceptually-Based Pairwise Image Distance)'를 사용했다. 이것은 두 VGG16 임베딩 사이의 '가중 차이(Weighted Difference)'로써 계산되며, 인간의 지각 유사성 판단과 일치한다.

잠재 공간 보간 경로를 선형 조각(Segment)들로 세분화하면, '조각난 경로들의 전체 지각 길이'를 '각 조각 간 지각 차이의 합'으로 정의할 수 있다. 물론 지각 경로 길이에 대한 자연스러운 정의는 이 합의 극한(즉, 무한히 잘게 쪼갠 것끼리의 차이의 합)일 테지만, 실제로는 $ε = 10^{-4}$ 정도의 크기를 사용한다. 모든 가능한 양 끝 점에 대한 잠재 공간 $Z$의 평균 지각 경로 길이는 아래와 같다.

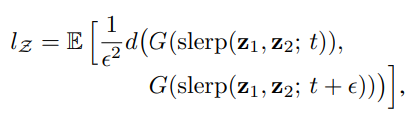
• $z_1$, $z_2$는 $P(z)$의 분포를 따르며, $t$는 0부터 1까지의 연속균등분포, $G$는 생성자, $d$는 결과 이미지 사이의 지각적 거리를 평가한다.
• $\text{slerp}$는 구면 보간(Spherical Interpolation)을 의미하며, Normalized된 입력 잠재 공간을 위한 가장 적절한 보간법이다.

우리는 얼굴의 특징에만 집중하기 위해 먼저 이미지를 크롭하여 얼굴 부분만 남겼으며, $d$는 Quadratic(2차)이므로 $ε^{2}$로 나눴다. 또한 대략 십만 개의 샘플로 기댓값을 구했다.

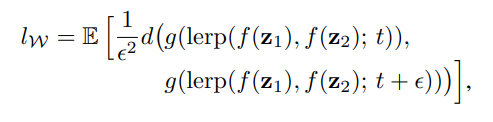
• 위 식은 $W$에서의 평균 지각 경로 길이를 계산하는 식으로, $Z$의 길이를 구하는 방식과 매우 비슷하다.
• 유일한 차이는 보간이 $W$ 공간에서 일어난다는 것이며, $W$의 벡터는 Normalized되지 않았기 때문에 선형 보간($\text{lerp}$)을 썼다.

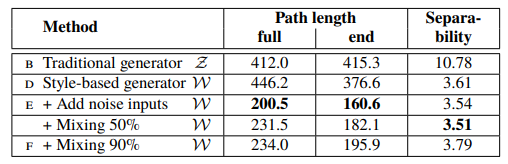
위 표를 보면 노이즈를 추가한 StyleGAN 생성자의 전체 경로 길이가 기존 생성자에 비해 훨씬 짧게 나타났다. 이건 $W$가 $Z$보다 지각적으로 더 선형적임을 뜻한다. 하지만 이 측정법은 입력 잠재 공간 $Z$에게 살짝 유리하다. $W$가 $Z$를 평평하고 Disentangled 하도록 매핑한 결과라면, 입력 다양체(Input Manifold)에 없는 지역을 포함할 수 있으므로 나쁘게 복원될 수 있는 반면, 입력 잠재 공간 $Z$는 정의에 의해 그러한 지역이 아예 없기 떄문이다. 즉 우리가 이 측정값을 경로의 끝점으로 제한한다면 $l_Z$에는 영향을 주지 않으면서도 더 작은 $l_W$을 얻을 수 있을 것이다.

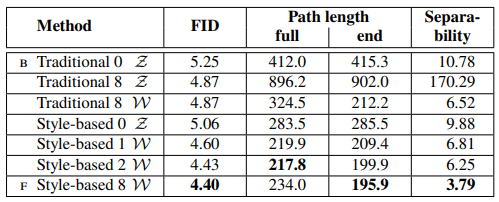
위 표는 경로 길이가 매핑 네트워크에 따라 얼마나 영향을 받는지를 나타낸 것이다. 기존의 생성자와 StyleGAN 생성자 모두 매핑 네트워크를 가지면 좋다는 것을 알 수 있으며, 깊이를 더하는 것도 지각 경로 길이와 FID를 향상시키는 것을 알 수 있다. 단, 기존의 생성자에서 $l_W$는 향상되나 $l_Z$는 상당히 나빠진다는 점은 흥미로운데, 이것은 입력 잠재 공간이 GAN에서 임의로 얽힐 수 있다는 우리의 주장을 보여준다.

✅ 서로 다른 잠재 공간 벡터를 뽑아서 만든 두 이미지가 얼마나 자연스럽게 보간되느냐를 또 하나의 성능 지표로 사용할 수 있으며, 그 수단으로 지각 경로 길이를 사용했다. 또한 기존 GAN과 StyleGAN 모두 생성자 매핑 네트워크를 추가하고 깊이를 늘리는 것이 좋게 작용했다.

4.2 Linear Separability

잠재 공간이 충분히 분리되어 있다면, 각 변동 요소에 상응하는 방향 벡터를 찾을 수 있다. 우린 이 효과를 정량화하는 또 다른 지표를 제안한다. 잠재 공간의 점들이 선형 초평면에 의해 얼마나 두 집합으로 잘 분리되는지를 측정하는 것이다. 분리된 각각의 집합은 이미지의 특정한 이진 속성과 상응하게 된다.

생성된 이미지들을 레이블링하기 위해, 우린 수많은 이진 속성에 대해 보조 분류 네트워크들을 학습시켰다. (ex. 남성과 여성의 얼굴 구분) 우리 테스트에서 분류기는 판별자와 같은 아키텍처를 가지고 있으며, CelebA-HQ 데이터셋을 통해 학습되었다. 한 속성의 분리성(Separability)을 측정하기 위해, 20만 개의 이미지를 생성한 후 보조 분류 네트워크를 통해 분류했다. 그리고 샘플을 분류 신뢰도(Classifier Confidence)에 따라 정렬하고 가장 점수가 낮은 절반을 제거하여 10만 개의 레이블링된 잠재 공간 벡터를 생성했다.

각 속성에 대해, 우린 선형 SVM을 학습시켜서 잠재 공간의 점(기존 생성자는 $z$, StyleGAN 생성자는 $w$)에 따라 레이블을 예측하고 점들을 평면으로 분류했다. 그리고 조건부 엔트로피 $H(Y|X)$를 계산했다. ($X$는 SVM에 의해 예측된 클래스, $Y$는 사전 학습된 분류기에 의해 결정된 클래스) 이는 샘플이 초평면의 어느 쪽에 놓여있는지 알고 있음을 가정하면, 표본의 실제 분류를 결정하기 위해 얼마나 많은 추가 정보가 필요한지를 나타낸다. 낮은 값은 상응하는 변동 요소에 대한 일관된 잠재 공간 방향을 암시한다.

📌 엔트로피(Entropy)와 조건부 엔트로피(Conditional Entropy)

• 엔트로피: $H(X)$로 표기하며, 어떠한 확률 변수의 값을 얼마나 예측하기 어려운지를 의미한다. ($H(X) = -P(X)\log{P(X)}$)

• 조건부 엔트로피: $H(Y|X)$로 표기하며, 어떤 확률변수 $X$가 다른 확률변수 $Y$의 값을 예측하는 데에 얼마나 도움이 되는지를 측정하는 방법 중 하나이다. (#)

우린 최종 분리성 점수를 $\exp(\sum_{i}H(Y_i|X_i))$로 계산한다. ($i$는 총 40개의 속성) '인셉션 스코어'에서와 유사하게, $\exp$ 항은 Logarithmic한 값을 비교하기 쉽게 선형 도메인으로 옮겨주는 역할을 한다.

📌 인셉션 스코어(Inception Score, IS)

FID와 같이 생성자로부터 생성된 이미지의 품질과 다양성을 평가하기 위한 지표이며, FID와 달리 오직 생성된 이미지의 분포만을 고려한다. 사전 학습된 이미지 분류 모델인 Inception v3을 활용한다. (#)

4.1 섹션의 표 2개는 $W$가 $Z$보다 일관적으로 더 잘 분리될 수 있다는 것을 나타낸다. 또한, 매핑 네트워크의 깊이를 늘리는 것은 이미지 품질과 $W$에서의 분리성을 향상시키는데, 이것은 합성 네트워크가 본질적으로 분리된 입력 표현을 선호한다는 가정과 일맥상통한다. 흥미롭게도, 매핑 네트워크를 기존 생성자 앞에 추가하는 것은 $Z$에서의 분리성에 심한 손실을 가했지만 중간 잠재 공간 $W$에서의 상황은 향상시켰다는 것이다. 이건 기존의 생성자 구조 역시 학습 데이터의 분포를 따르지 않아도 되는 중간 잠재 공간을 도입할 때 더 잘 작동한다는 것을 보여준다.

✅ 이진 속성이라면 두 가지 값 중 하나를 갖는 속성이라는 건데, 이 역시 매핑 네트워크를 사용하여 중간 잠재 공간을 만들어 사용하면 (다른 속성들과 얽히지 않고) 뚜렷하게 잘 분리되는 속성을 얻을 수 있다고 말하는 것 같다.

5. Conclusion

우리가 보인 결과와 비슷한 연구에 근거하여, 전통적인 GAN 생성자는 스타일 기반의 설계보다 모든 면에서 열등하다는 것이 확실해지고 있다. 확립된 품질 지표 면에서 이건 사실이고, 우린 고수준 속성의 분리와 확률론적 효과, 중간 잠재 공간의 선형성에 대한 우리의 연구가 GAN 합성에 대한 이해와 제어 가능성을 향상시킬 것이라 믿는다.

우린 우리의 평균 경로 길이 지표가 훈련 중에 Regularizer로 쉽게 쓰일 수 있다는 점에 주목했다. 또한 선형 분리 가능성 지표의 몇몇 변종도 같은 일을 할 것이다. 일반적으로, 우린 훈련 중 중간 잠재 공간을 직접 형성하는 이 방법이 미래의 연구에 흥미로운 길(Avenues)을 제공할 것으로 기대한다.

---

요약

기존 GAN과 구별되는 StyleGAN의 대표적인 구조적 특징은 이렇다.

• 중간 잠재 공간: 초기 잠재 공간을 바로 생성자의 입력으로 사용하지 않고 매핑 네트워크를 한 차례 거친 것을 사용함으로써 잠재 요소들이 서로 더 잘 분리(Disentanglement)되게끔 한다.
• AdaIN 연산: 중간 잠재 코드로 만든 스타일을 생성자 네트워크의 각 블록에 주입하기 전, 정규화를 포함한 AdaIN 연산을 수행하여 스타일의 국소화를 유도한다.
• 노이즈 입력: 네트워크의 각 블록마다 노이즈를 주입함으로써 생성된 이미지에서 확률론적인 부분들을 각각 제어할 수 있다.

또한, 새로운 생성자의 분리성을 평가하기 위한 다음 두 지표도 소개되었다.

• Perceptual Path Length(지각 경로 길이): 서로 다른 두 잠재 코드로부터 생성된 이미지가 서로 얼마나 자연스럽게 보간되는지를 측정한다.
• Linear Separability(선형 분리성): 잠재 공간의 각 변동 요소들이 얼마나 선형적으로 뚜렷하게 분리될 수 있는지를 평가한다.

📖 도움이 된 자료

• [서운산미디어센터] Style GAN Review - StyleGAN에서 사용된 구조나 기법들이 '왜 필요한지'를 직관적으로 느낄 수 있게 해준 영상이다.