Modern Convolutional Neural Networks

부스트캠프 ai tech 3주차에 배운 내용을 정리하는 글입니다.

모델의 파라미터 수가 늘어날수록 학습이 어렵고 generalization performance가 떨어진다고 알려짐 → 그렇기 때문에 파라미터 숫자를 줄이는 여러 테크닉이 존재

어떤 모델을 봤을 때 파라미터가 대략 어느 정도 되는지 셀 수 있는 감이 필요

• ILSVRC(ImageNet Large-Scale Visual Recognition Challenge)
  • classification / detection / localization / segmentation
  • 1,000 different categories
  • over 1 million images
  • training set: 456567 images

---

아래 모델들의 파라미터 수, 깊이를 주의 깊게 보자

결론적으로 파라미터 수는 점점 줄고 깊이는 점점 깊어지고 성능은 점점 좋아짐 → 어떻게? → 네트워크를 깊게 쌓으면서 파라미터 수를 줄이는 테크닉들이 있음

1. AlexNet

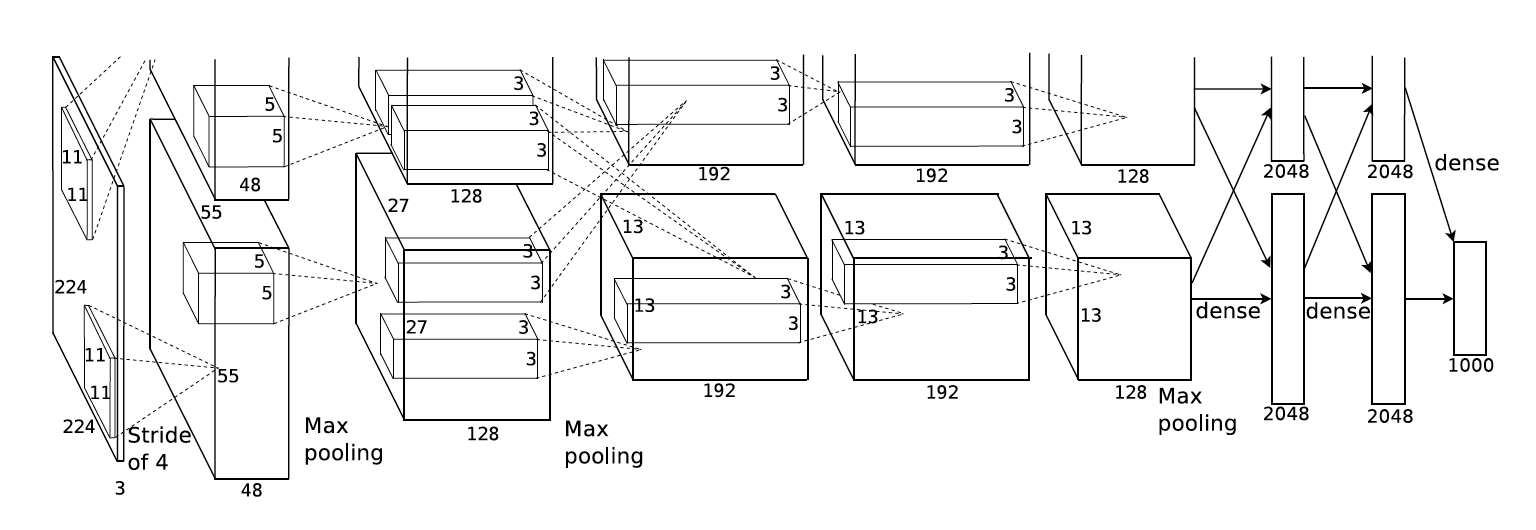
• 특징

  • 당시 GPU가 부족했기 때문에 네트워크가 2개로 나눠져 있음
  • 11 by 11, 5 by 5, 3 by 3 filter을 사용함 → 파라미터의 수 관점으로 봤을 때 11 by 11 filter은 좋지 않음
    • 5 convolutional layers + 3 dense layers

• key ideas

  • ReLU를 사용함
    • 0보다 클 땐 그대로, 0보다 작을 땐 0 → linear model의 장점을 가지고 있음
    • easy to optimize with gradient descent
    • good generalization
    • sigmoid, tanh는 0보다 커질수록 or 작아질수록 기울기가 줄어들게 됨 → vanishing gradient problem → ReLU는 이런 문제를 없애줌
  • 2개의 GPU를 사용함
  • Local response normalization, Overlapping pooling(겹치게 pooling. pooling에 사용되는 filter의 크기 > stride)
  • Data augmentation
  • Dropout

지금 생각하면 당연한 것들이지만 2012년도에 나온 걸 생각하면 대단

2. VGGNet

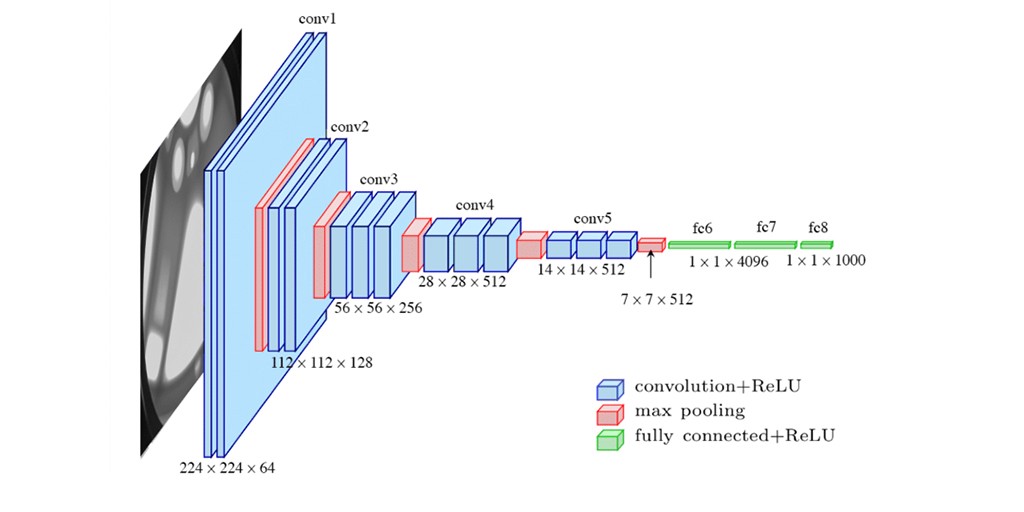
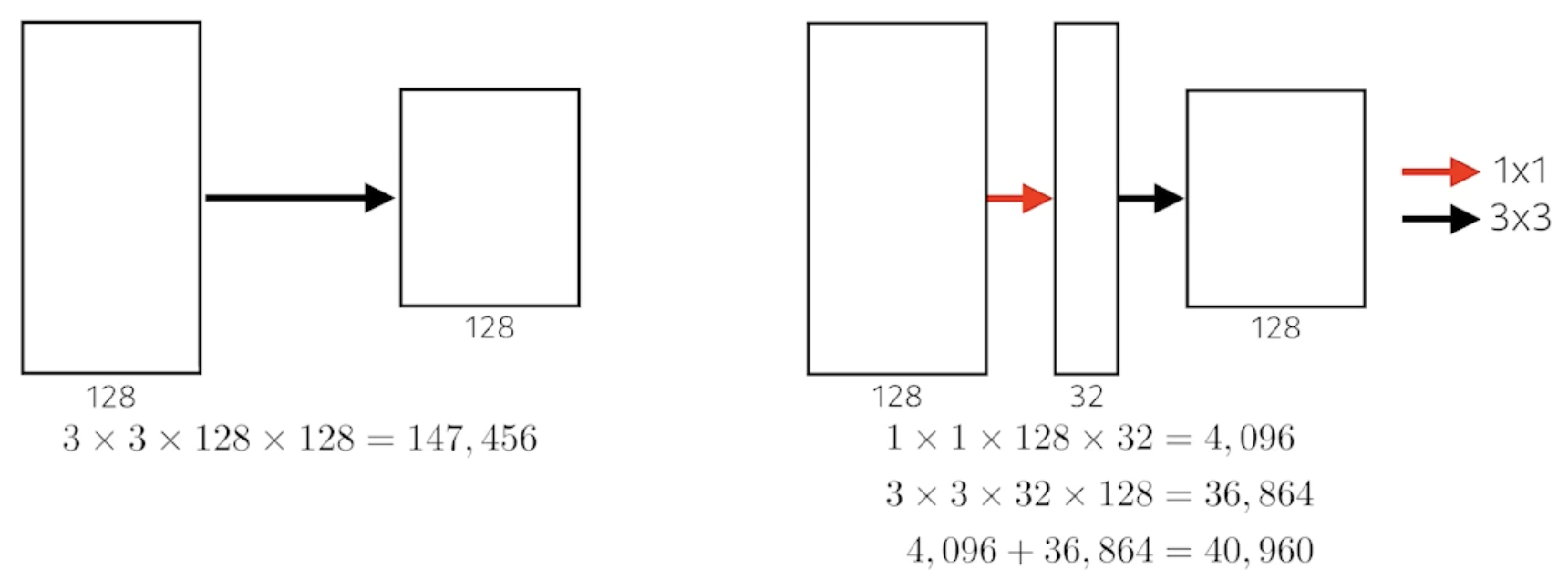
• 3 by 3 convolution filters(with stride 1)만 사용함 → 이게 중요
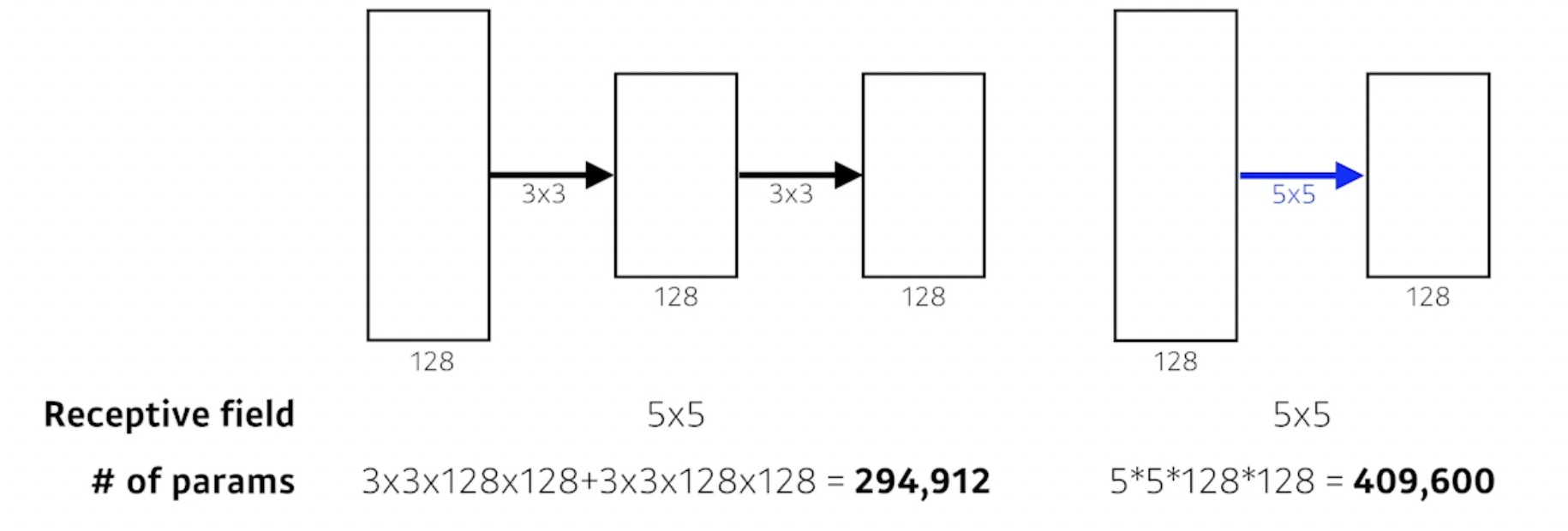
  • 3 by 3을 두 번 사용했을 때 파라미터 수와 5 by 5를 한 번 사용했을 때 파라미터 수
    

• 1 by 1 convolution for fully connected layers(파라미터 수를 줄이려고 사용한 것은 아님)
• dropout (p = 0.5)
• layer 수에 따라 VGG16, VGG19
  

3. GoogLeNet

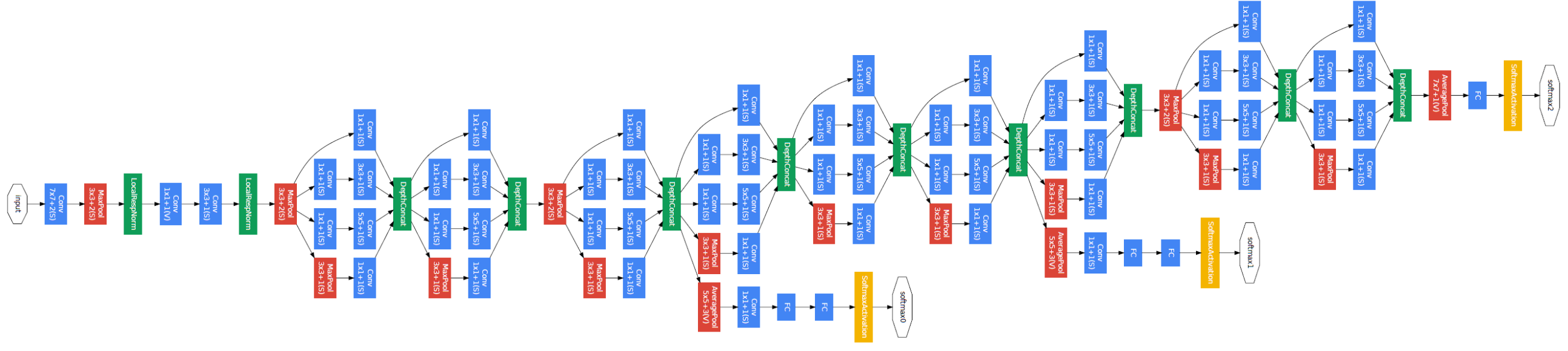
• 22 layers
• 비슷하게 생긴 네트워크가 반복됨(network in network, NiN 구조)
• inception blocks: 입력이 여러 갈래로 퍼졌다가 다시 합쳐짐
  

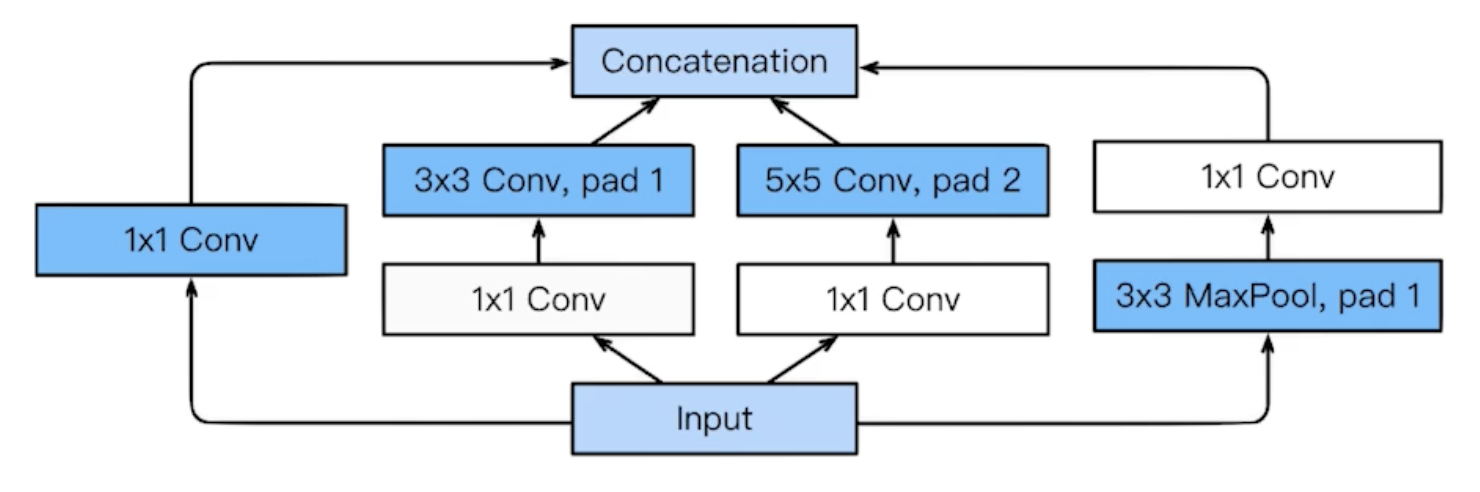
• 1 by 1 convolution 사용(위 그림에도 나옴) → demension reduction의 효과가 있음 → 여기서 demension은 channel을 의미(channel: tensor의 spatial dimension(width, height)이 아닌 tensor의 depth) → depth를 줄임으로써 파라미터 수를 줄임
  

4. ResNet

뉴럴 네트워크가 깊어질수록 훈련하기가 힘듦 → overfitting이 발생할 줄 알았는데 아니었음 → degradation problem(optimization 문제) 발생

→ identity map을 추가함

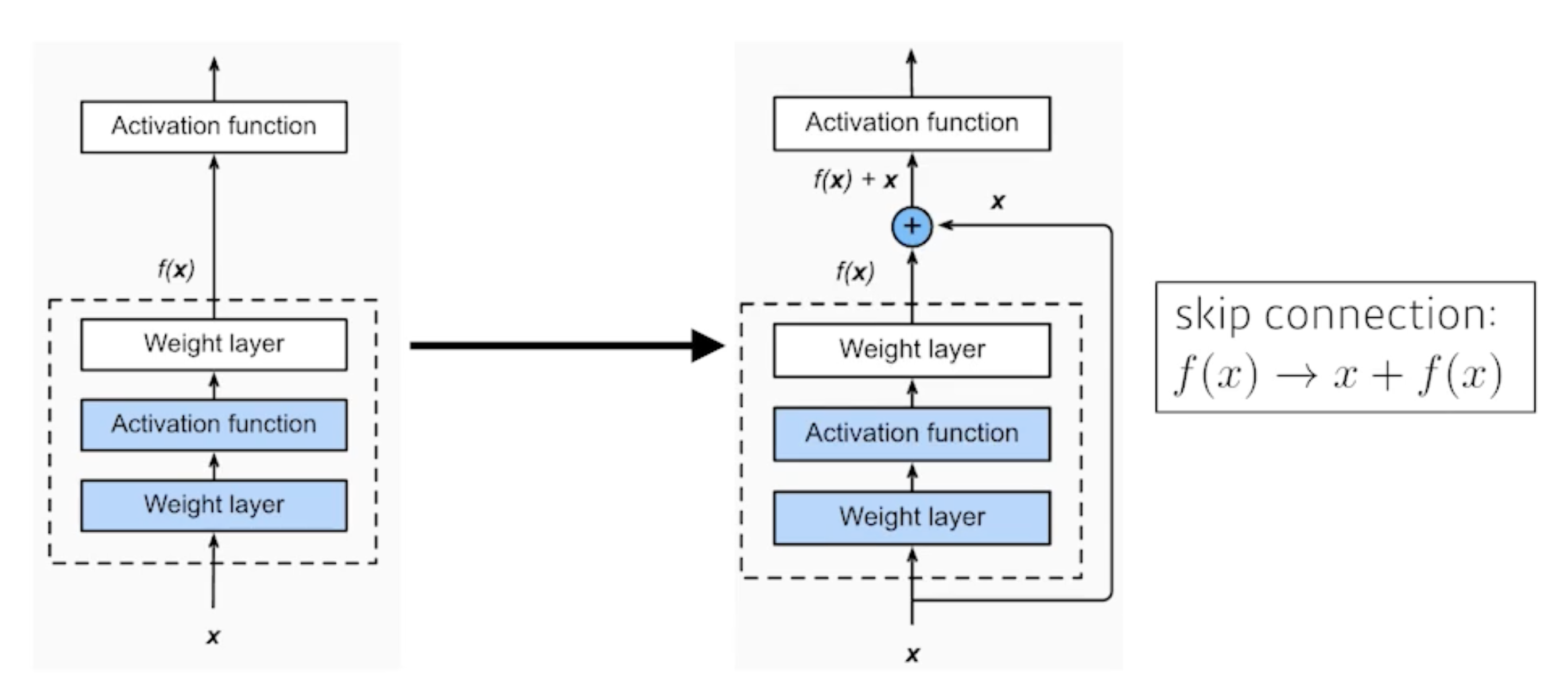
input x가 들어가서 output f(x)가 나왔는데 그 output f(x)에 input x를 더해줌 → 왜? 차이(residual)만 학습시키려고

target function: $H(x) = F(x) + x$

residual function: $F(x) = H(x) - x$

$x$에서 바로 $H(x)$와의 관계를 학습하기엔 복잡하니까 $x$(identity)를 살리고 나머지 잔여 부분 $F(x)$만 학습하게끔 하면 학습의 부담을 줄일 수 있지 않을까? 하는 생각에 제안
→ $H(x)$가 복잡하더라도 적어도 자기 자신($x$)에 대한 보존은 신경 쓰지 않아도 되니까(back propagation을 할 때도 경로가 2개임!! layer들을 지나가는 경로와 skip connection 경로 → layer들을 지나가면서 gradient vanishing 문제가 발생해도 skip connection 경로를 통해 identity가 보존되므로 괜찮음. 그리고 이러한 residual 블록이 여러 개 쌓이면 gradient가 지나갈 수 있는 경로는 2배씩 늘어남)

→ 이렇게 하니까 깊은 네트워크도 학습을 시킬 수 있게 됨

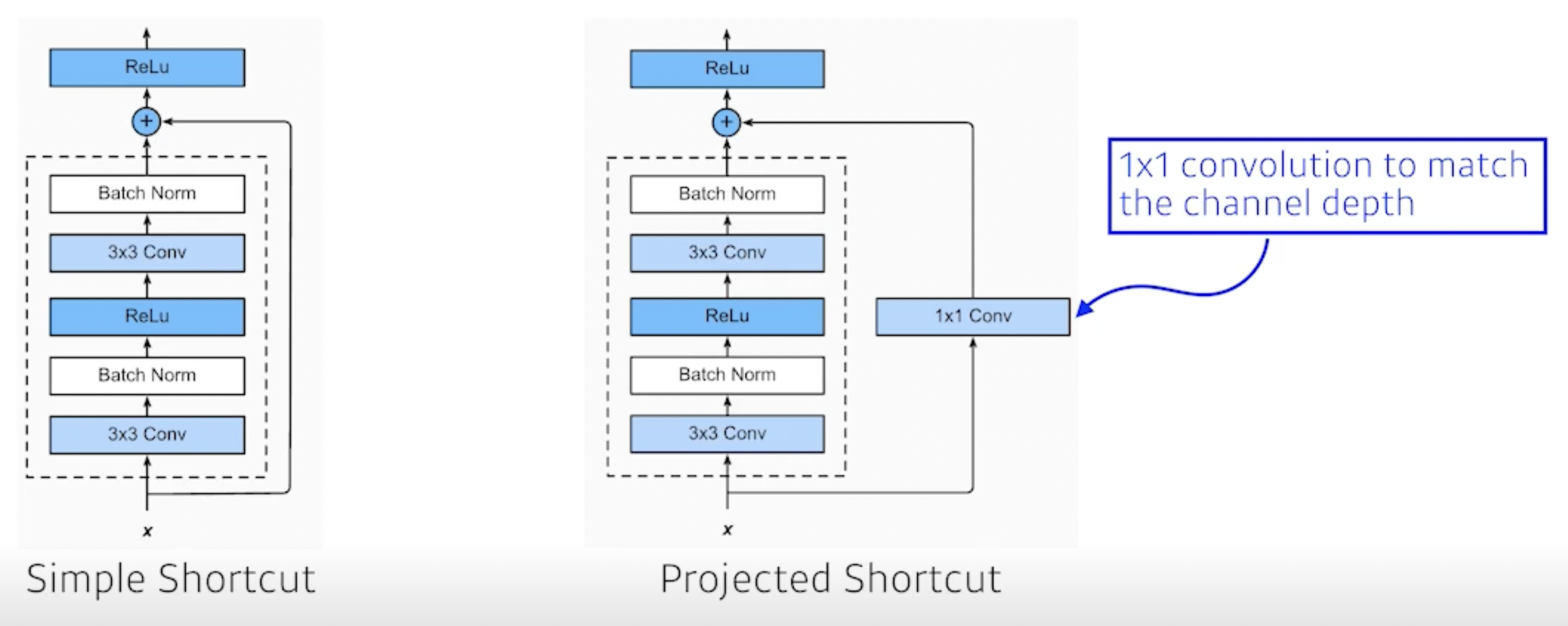
output과 input을 더하기 위해서는 서로 차원이 같아야겠지 → 위 그림과 같이 1 by 1 filter로 channel을 맞춰줌

• bottleneck architecture

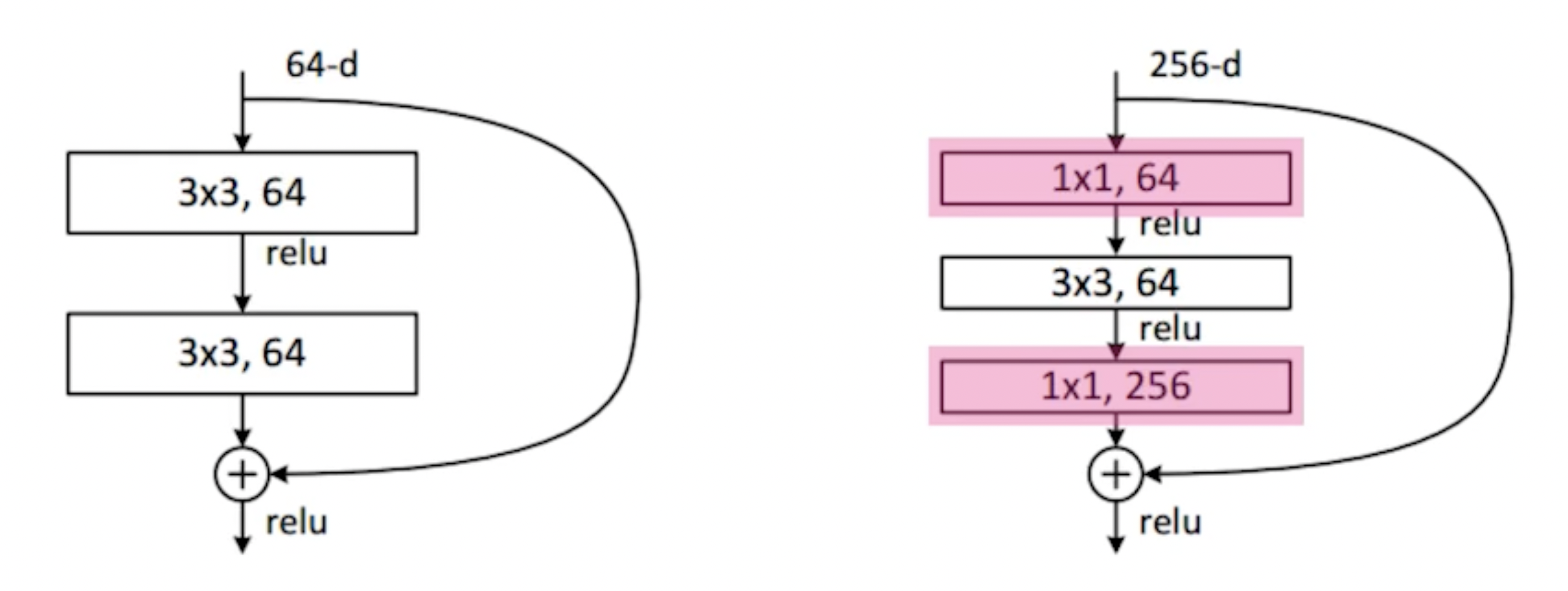
3 by 3 convolution 하기 전에 1 by 1으로 input channel 줄이고 3 by 3 convolution 한 뒤에 1 by 1으로 다시 input channel 늘려줌(오른쪽의 3 by 3 입장에서는 input / output의 dimension이 감소 → bottleneck)

5. DenseNet

• Dense Block
  • input과 output을 더하지 말고 합치자
  • 채널 수가 기하적으로 증가
• Transition Block
  • BatchNorm → 1 by 1 conv → 2 by 2 AvgPooling
  • Dimension reduction

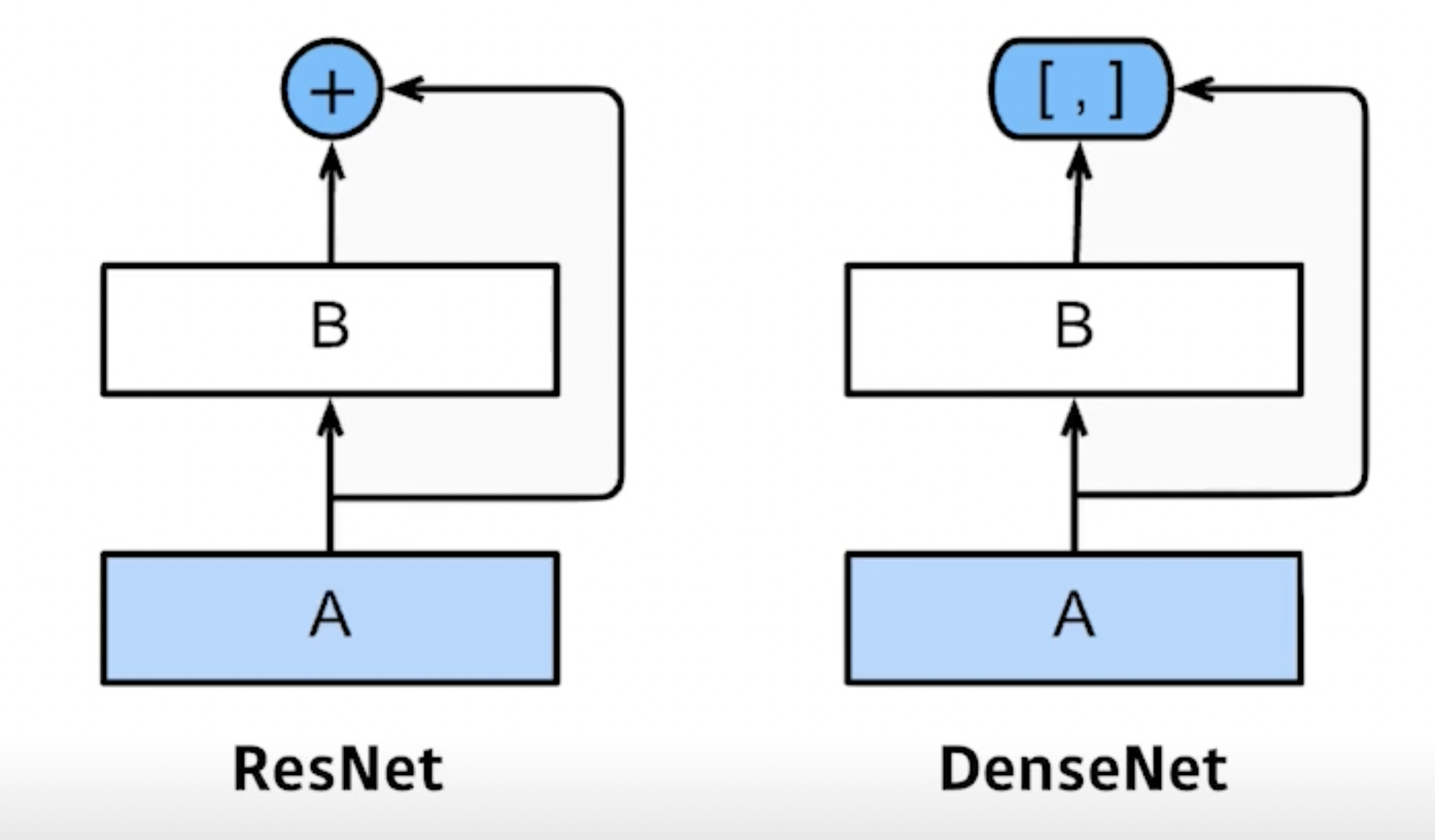
Dense Block: ResNet처럼 input과 output을 더하면 값이 섞이니까 그냥 concatenation 하자 → 문제는 합친 것을 또 합치기 때문에 channel이 2배, 4배, 8배… 커짐 → 얘를 위해 파라미터 수가 증가

$x → [x, f_1(x)] → [x, f_1(x), f_2(x, f_1(x))] → …$

Transition Block: 파라미터 수가 증가하는 문제를 해결하기 위해 중간중간 채널을 줄여줌