이번에 공부한 수 체계는 Ring이다. Ring은 set에 +와 를 적당히 잘 정의한 수체계다. +와 를 어떻게 정의해야 우리는 ring이라고 부를 수 있을까? 그 8가지 조건이 아래에 나와있다.
8가지 조건 외에도 두 가지 조건, commutative multiplication, ring with identity라는 조건이 있는데 이 조건이 만족하면 또 좋은 성질을 가진 수체계를 정의할 수 있다.



Integral Domain과 Field의 정의가 정의돼있다. Field에는 안 적어놨는데 모두 commutative ring with identity에서 정의된다.
간단히 Integral Domain은 어떤 곱해져서 만들어진 수가 0이라면 그 곱한 수 중 하나는 0이여야 한다는 의미이다. 예를 들어 실수집합 R이 있겠다. 아닌 예는 뭐가 있을까? 앞서 본 Z6을 떠올려볼까. Z6은 modulo6으로 같은 수들의 집합이 각 원소가 되는 집합이다. 2*3 in Z6은 0이다. 그러나 2와 3 둘 중에 하나도 0이 없기 때문에 Integral Domain이 아니라고 할 수 있겠다.
Field는 뭐라고 할 수 있을까? ax = xa =1? 요건 앞에서 살펴본 unit의 성질과 같다. a가 0이 아니라면 모두 unit이라는 뜻이다.
이것도 예를 들어 실수집합 R이 있다. 2에 대해 1/2이 있어서 곱했을 때 1이 되고 0이 아닌 x에 대해 1/x이 존재하기 때문이다.
Field가 아닌 예는 정수집합 Z가 있겠다. 너무 당연하게도 1하고 -1외에는 unit이 없다.
후술하겠지만 모든 Field는 IntegralDomain이다. 그리고 모든 finite Integral Domain은 Field이다.
또! Integral Domain에는 zerodivisor가 없다. 아래를 참고하자.


zerodivisior가 아니라는 얘기는 아님 부분을 수정해야한다. field면 integral domain이므로 zerodivisor가 아니다.
Cartesian product가 ring이 되는 방법이 기술돼있다. 그냥 우리가 쉽게 생각할 수 있는 방식으로 +와 *를 정의해도 깔끔하게 ring으로 만들 수 있다.
만약 어떤 set의 Subset이 ring이 된다면 어떨까? 우리는 그를 subring이라고 부른다. Subring이 되기 위해선 4가지 조건을 만족해야 한다. +와 *가 subset에서는 자명하게 유지될 것이기에 그 계산결과들이 잘 집합에 속해있는지만 확인하면 되겠다. commutativity, associativity 요런건 확인할 필요가 없다는 것이다!
나중에 가면 더 쉽게 closure under Substitution과 closure under multiple만 보여도 Subring이라는 것을 증명할 것이다!

우리는 앞서 ring의 조건에 a+x = 0R을 만족하는 x가 항상 존재해야 한다고 했다. 그런데 여기선 그 x가 unique함을 보여주고 있다. u와 v가 동시에 만족한다고 할 때 u = u+0 = u+a+v = (u+a)+v (associativity) = (a+u)+v (commutativity) = 0 + v = v 즉 u=v. 너무 easy하다.
참고로 우리 코딩소학회 회장님 이름이 '이지'다.
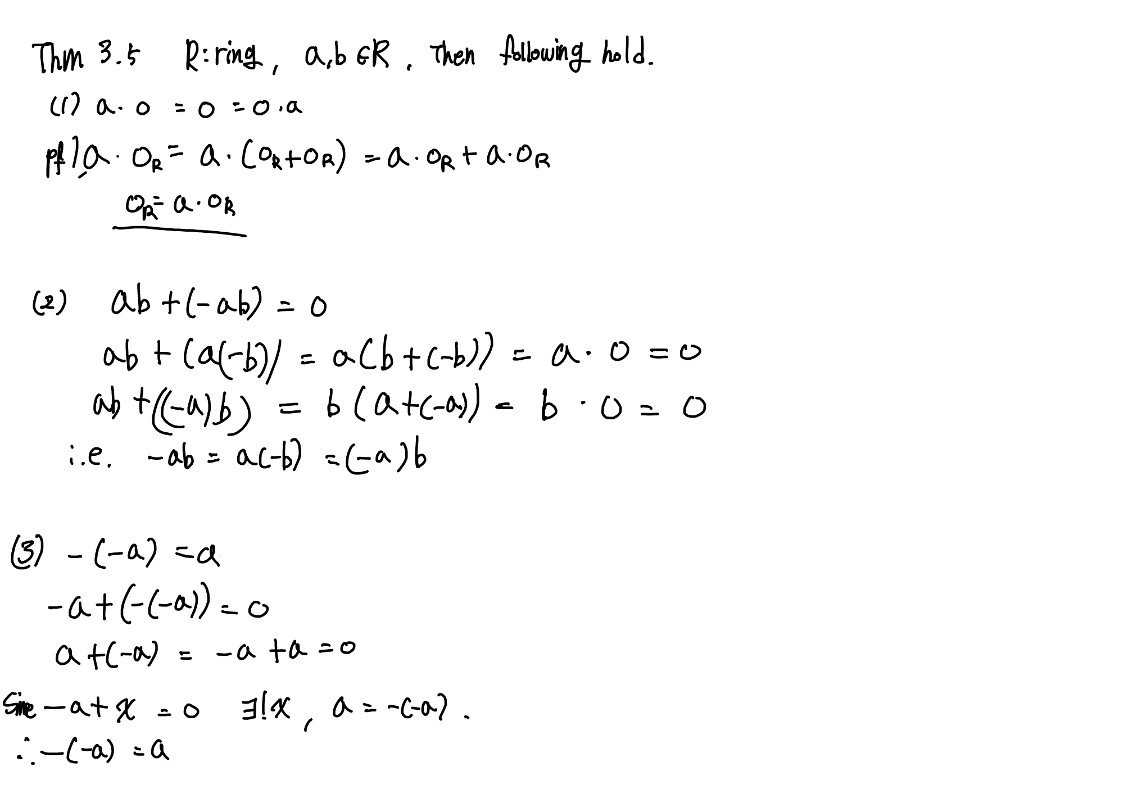
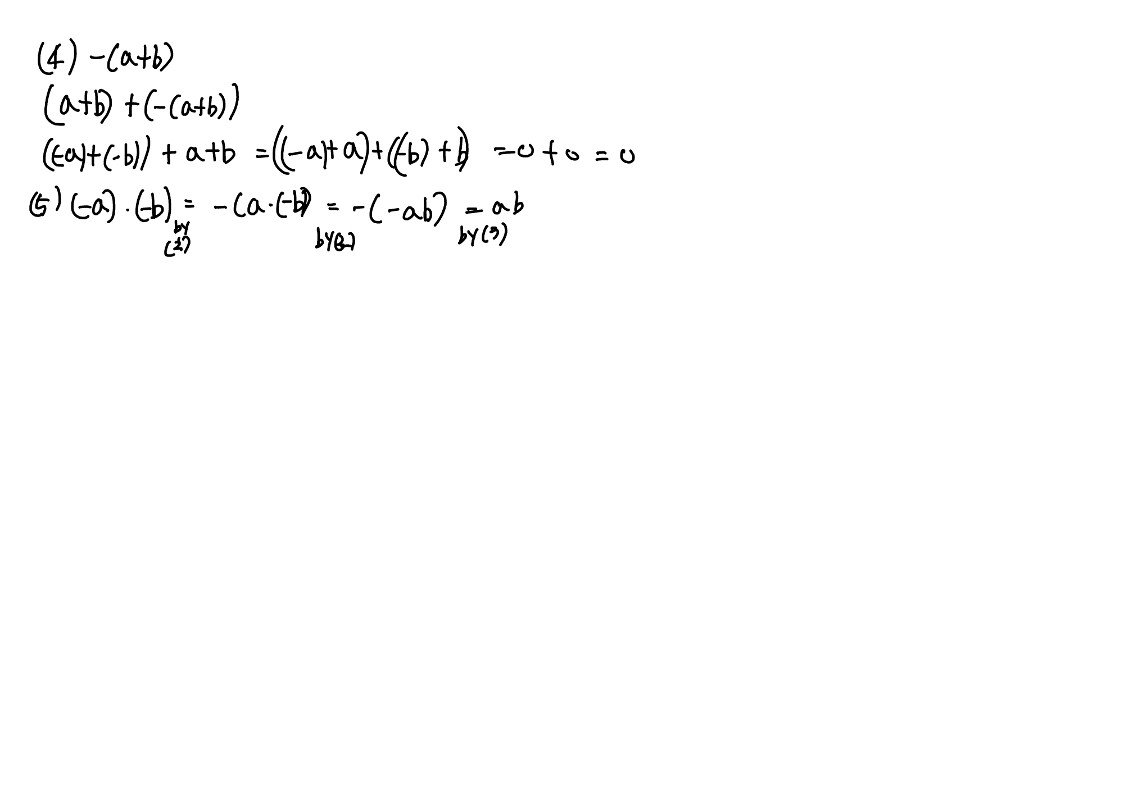
위는 ring의 너무나 당연해보이는 성질이다.
Ring은 정말 중요하다. 잘 공부 좀 해놓자.
