6.3 Prime ideal and Maximal ideal

JUHONGYEE·2022년 6월 4일

수학 현대대수

열심히 올리는 현대대수

목록 보기

18/24

서론

이번 시간에는 Quotient ring이 field가 되고 integral domain이 되는 조건인 Prime ideal과 Maximal ideal에 대해 알아보겠습니다.

Prime idal

def of Prime ideal

An ideal P in R is called prime if
(1) P≠R
(2) ab∈P ⇒ a∈P or b∈P

현재까지의 정의는 우리가 알고 있는 소수의 정의와 매우 비슷합니다. 대신 P는 전체 집합과 크기가 같지는 않아야하는데 이는 전체집합이 그러면 자연스럽게 R이 되는데 별로 재미있는 논의는 아니기 때문입니다.

example of Prime ideal

R = ℤ, P⊆R : ideal generated by a prime p∈ℤ.

현재 상황은 우리가 잘 알고 있는 prime number 하나를 선택하여 그로부터 generate한 ideal에 대해 얘기하는 상황입니다.
이 ideal은 prime이 된다고 하는데 살펴봅시다.

Let ab∈P = (p). ab∈(p) ⇔ P|ab ⇒ P|a or P|b (∵P is a prime) ⇒ a∈(p) or b∈(p).

정의처럼 ab가 P에 속한다면 a가 P에 속하거나 b가 P에 속하게 됩니다.

R : integral domain, P = (0)
integral domain의 첫 번째 조건 1과 0이 달라야합니다. 그러므로 1은 (0) 집합에 속하지 않습니다.
또한 ab = 0 이면 a=0 or b=0조건에 따라 ab∈P에 속하면 a∈P or b∈P입니다. 자명하게 integral domain에서 (0)은 prime입니다.
R = ℤ[x], P = (x)
한가지 상기할 조건이 있는데 어떤 ideal이 전체집합이라면 그 ideal은 (1)입니다. 즉, 1이 그 내부에 속합니다. 만약 1이 속하지 않는다면 전체집합이 아닙니다. 그러므로 prime ideal인지 확인해주기 위해서는 1이 속해있는지 항상 확인해주어야합니다.

이번 ideal P는 x로 generate되었기 때문에 1이 속하지 않습니다. 그러므로 전체집합이 아니라는 Prime ideal의 1번 조건은 만족한 셈입니다.

그러면 2번 조건을 확인해봅시다
f(x)g(x)∈P ⇒ x|f(x)g(x) ⇒ x|f(x) or x|g(x)(∵x is irreducible) ⇒ f(x)∈P or g(x)∈P
즉 P는 prime ideal입니다.

Thm 6.14 Prime ideal과 integral domain

P is a prime ideal ⇔ R/P is an integral domain.

증명에 앞서 그 의미를 생각해봅시다. P가 prime ideal이라는 것은 R/P가 integral domain인것과 같다고 합니다. 앞서서 우리는 P로 quotient ring을 만들 때, natural homomorpism을 잡으면 kernel이 P가 됨을 보였습니다.

이 때 prime의 성질과 integral domain의 성질은 너무나도 유사합니다. ab가 P에 속하면 a가 P에 속하거나 b가 P에 속해야하는데 여기서 P에 속하면이라는 표현을 0이면 이라는 표현으로 바꾸면 정확히 integral domain의 속성입니다. 또한 R/P에서는 P의 원소들이 0과 같게 여겨지기 때문에 R/P는 integral domain이 될 수 밖에 없음이 직관적으로 보일 것입니다.

증명해봅시다.

proof)

먼저 prime의 1번 조건 전체집합이 아니다와 integral domain의 1번 조건 0과 1이 다르다가 동치임을 보이겠습니다.

prime의 1번 조건 전체집합이 아니다는 즉 1이 P에 속해있지 않음을 의미합니다. 그런데 1이 P에 속해있지 않다는 것은 즉 0+P≠1+P in R/P임을 의미합니다. 즉, integral domain에서의 0과 1은 다릅니다.
(반대방향도 동일합니다.)
prime이 2번 조건 ab∈P ⇒ a∈P or b∈P 와 integral domain의 2번 조건 ab = 0 ⇒ a=0 or b=0이 동치임을 보입시다.

(⇒)
prime의 2번 조건이 성립한다고 합시다. 이 때 ab+P = 0+P라고 가정하면 ab∈P in R이고 a∈P or b∈P이므로 a+P = 0+P or b+P = 0+P in R/P입니다.

(⇐)
integral domain의 2번 조건이 성립한다고 합시다. 그러면 ab∈P라고 가정할 때 ab+P = 0+P이고 integral domain의 조건에 따라 a+P = 0+P or b+P = 0+P이므로 다시 a∈P or b∈P가 되어 prime ideal이 잘 성립합니다.

위에 말로 풀어놔서 오히려 헷갈릴 수 있는데 정말 별게 아닙니다. 아래 수식을 봅시다.

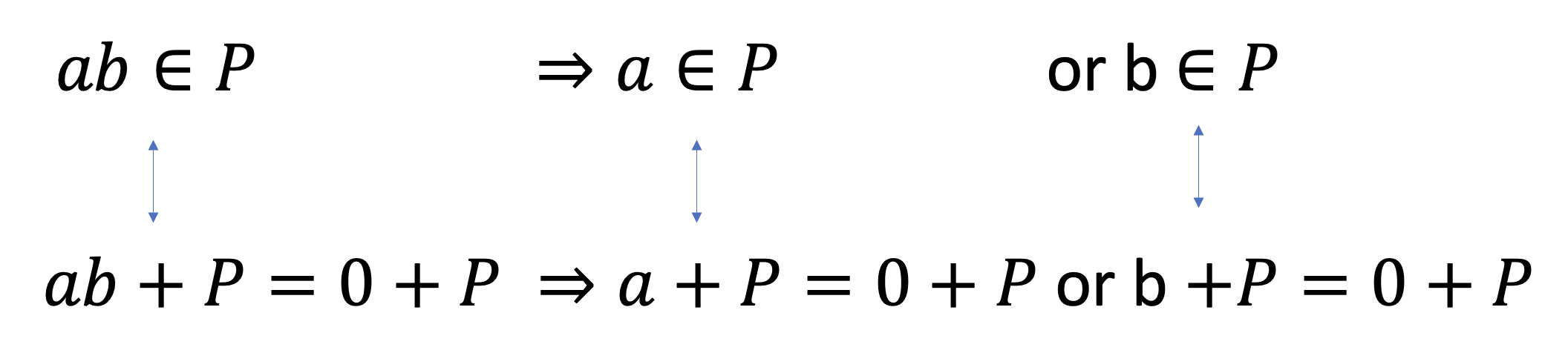
그냥 이 표현들이 다 같은 말 일 수 밖에 없습니다. 왜냐면 R/P에서 P는 0을 나타내기 때문입니다.

Maximal ideal

Maximum과 Maximal

간단하게 구분하고 넘어갑시다. Maximum은 전체에서 가장 큰 것(모든 것들과 비교 가능하고 제일 큰 것) Maximal은 비교할 수 있는 것 중 가장 큰 것이며 이 내용은 partial ordered 내용을 참고하시기 바랍니다.

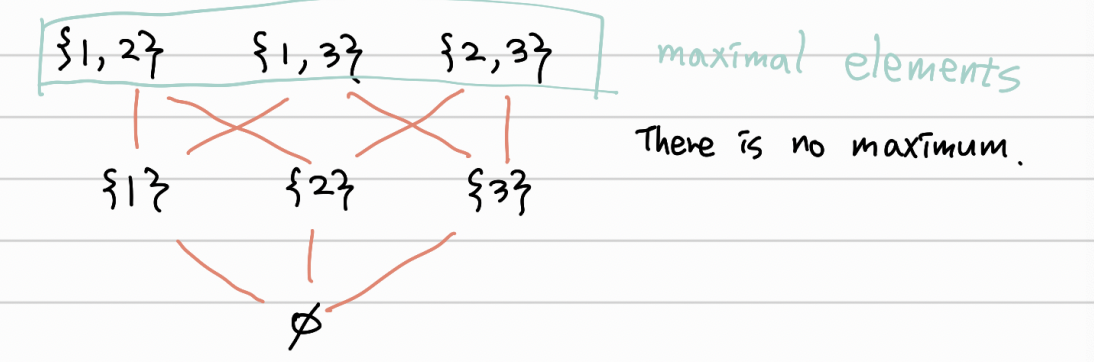
위의 그림에서은 집합의 포함관계를 표현한 그림입니다. 어떤 집합의 subset은 그 집합보다 작다고 여기는 것인데, 이 그림에서 전체 모두 비교가능한 Maximum은 없습니다. 다만 비교 가능한 것 중 가장 큰 것인 Maximal은 3개 존재합니다.

def of Maximal ideal

An ideal M in R is called maximal if
(1) M ≠ R
(2) If J is an ideal s.t M⊆J⊆R, then J=M or J=R

maximal ideal M은 전체집합이어서는 안됩니다. 그러면 그냥 maximum이 되어버리기 때문이고 또한 재미가 없습니다. R은 아니면서 즉 R의 proper subset이면서 최대의 subset이 되는 ideal을 maximal ideal이라고 부릅니다.

example of Maximal ideal

R = ℤ. M = (3)

(3) ≠ ℤ
Let J be an idela such that (3)⊆J⊆ℤ.
we will assume (3)⊊J and show that J=ℤ.
Pick a∈J with a∉(3) ⇒ gcd(a,3) = 1.

Then ∃u,v∈ℤ such that au+3v = 1.
⇒ 1∈J ∴J=R

R = ℤ[x], I = (x)
Since (x) ⊊(x,2)⊊ℤ[x], I is not maximal.

Thm 6.15 Maximal ideal과 field

Let M be an ideal in R. Then
M is a maximal ideal ⇔ R/M is a field.

M is a maximal ideal	R/M is a field
1)I ≠ R	i)0+M ≠ 1+M
2)M ⊊ J ⇒ J = R	ii)a+M ≠ 0+M ⇒ ∃b+M s.t (a+M)(b+M) = 1+M

증명해봅시다. 이 사실을 알고 가면 증명이 너무 당연하게 받아들여지는데 a가 M에 속해있다는 것(a∈M)은 a+M = 0+M이라는 의미와 같다.

proof sketch)

1) ↔︎ i)
I가 R이 아니라는 것은 1이 I에 속해있지 않다는 것과 같은 의미입니다. 그러므로 0+M과 1+M은 다를 수 밖에 없습니다. 그런데 반대로 0+M과 1+M이 다르다는 것은 I에 1이 속해 있지 않다는 의미이므로 I는 R이 아닙니다.

2)↔︎ ii)

⇐)
J가 M은 아니면서 M을 포함하는 ideal이라고 가정해봅시다.(M⊊J) 그렇다면 J에는 M에는 속하지 않으면서 J에는 속하는 원소 a가 존재합니다. ii)에 의해 M에 속하지 않는 b라는 원소가 존재해서 (a+M)(b+M) = 1+M입니다. 즉, (ab-1)+M = 0+M입니다. ∃m∈M ab-1 = m. ab = m+1.() 그런데 m+1은 M에 들어있을 수 없습니다. M은 1을 포함하지 않는데 m+1괴 m을 포함하면 그의 subtraction인 1을 포함하기 때문입니다. 그러므로 ab는 다시 J에 속합니다. 여기서 ab도 J에 속하고 m도 J에 속하므로 ()에 의해 1도 J에 속합니다. J는 ideal이기 때문에 1을 포함하면 전체집합임을 알 수 있습니다.

⇒)
2)의 사실이 참이라고 가정할 때 ii)임을 보여봅시다.
a+M ≠ 0+M 이라고 가정합시다. 그렇다면 a는 M에 속하지 않습니다. 그렇다면 J 라는 집합을 M+(a) = {m+ra|m∈M,r∈R}이라고 해봅시다. 그렇다면 J가 ideal입니다.

J가 ideal 임을 증명하고 넘어값시다.

closure under subraction은 너무나 자명하니 넘어가겠습니다.
ideal의 property를 증명해봅시다.
b∈R,k∈J라고 할 때 bk∈J이면 J는 ideal입니다.
k는 어떤 $m_1,r_1$ 에 대해 $m_1+r_1a$ 입니다. 이때 $bk = bm_1+br_1a$ 입니다. 이 때 $m_1$ 은 ideal의 원소이므로 R의 원소 b를 가져와도 $bm_1$ 이 다시 M에 속합니다.(def of ideal) 또한 R은 ring이므로 $br_1$ 도 다시 R의 원소입니다.(closure under multiple)

그러므로 bk∈J입니다. 즉, J는 ideal입니다.

J가 ideal이므로 M+(a)는 R입니다.(가정)
그렇다면 R에는 1이 속하므로 1∈M+(a)입니다. 즉 ∃ $m_2,r_2$ s.t $1= m_2+ar_1$

이는 $1+M = ar_2+M$ 임을 의미합니다. 이 때 $1+M≠0+M$ 이므로 $ar_2+M = (a+M)(r_2+M)$ 에서 $r_2+M$ 은 $0+M$ 이 아닙니다. 만약 $0+M$ 이라면 $1+M = 0+M$ 이 되기 때문에.

그러므로 R/M은 field입니다.

example

R = ℤ[x], I = (x,2). Define f:ℤ[x]→ $ℤ_2$ by f( $a_nx^n+...+a_1x+a_0$ ) = $a_0$

Then ker f = I. By the first isomolphism theorem, R/I≅ $ℤ_2$ .
Since R/I is a field, I is maximal.

위의 example을 통해 알아보는 maximal ideal 구별법.

0)어떤 ring R과 ideal I가 있을 때(조건)
1)어떤 ker f = I를 만족하는 f:R→S를 잡는다.(f도 잡고 S도 잡고)
2)이 때 S를 field로 잡으면 R/I와 isomolphism이고(by first isomolphsim thm) R/I가 field가 되므로 I가 maximal이 된다.

핵심은 field인 S와 kef f가 I인 f를 잡아주는 것.
S는 별로 안 어려울 것 같은게 R/I와 Isomolphism이므로 R/I를 잘 관찰하면 S가 잘 보이지 않을까 싶네요.

끝.

신기방기하네유 ㅎ