7.1 Definition and Examples of Groups

JUHONGYEE·2022년 6월 5일

열심히 올리는 현대대수

목록 보기

19/24

서론

group은 현대대수에서 다루는 매우 중요한 대수구조입니다. 그런데 ring이 우리가 보기에 굉장히 직관적인 것과 반대로 group 조금 더 추상적일 수 있습니다. 우리가 잘 생각하지 못하는 것들에 연산을 부여하여 연산을 하기도 하고 ring보다 연산이 하나가 적기 때문에 제약조건이 적어 특이한 것들이 자주 나올 수 있습니다. 그럼에도 불구하고 수학을 해석해나가기에 매우 중요한 group에 대해 배워보겠습니다.

Definition of Examples of Groups

Example of Groups

그룹에는 다양한 예시가 있습니다. 그 중에 이해하기 쉽고 중요한 예시로는 우리가 잘 알고 있는 permutation입니다. 고등학교 확률과 통계 시간에 질리도록 공부했던 이 permutation은 사실은 group으로 표현할 수 있습니다. 우리가 사용하는 permutation의 정의는 다음과 같습니다.

the act or process of changing the linear order of an ordered set

먼저 T = {1,2,3}
이 permutation들을 모두 모아보겠습니다.

123 132 213 231 312 321

이 각각의 ordering들에 대해 T의 원소를 각 ordering으로 대응시키는 하나의 bijective function을 생각할 수 있습니다.

예를 들어 f(1) = 2, f(2) = 1, f(3) = 3이라고 하면 f는 f(1)f(2)f(3)이라는 ordering을 정의하게 해줍니다. 그 ordering은 213이지요.

이때 이 f들의 특성을 살펴봅시다.

f들은 총 6개가 존재할텐데요 각각을 다음과 같은 notation으로 쓰겠습니다.

$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$ , $\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$ , $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$

$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$ , $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}$ , $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$

각각은 1,2,3을 바로 아래의 원소로 대응시킨다는 의미입니다.
(이거 조금 헷갈릴 수 있는데 예를 들어 2번째 함수 의미가 첫번째 원소 그대로 두고 두번째 세번째를 바꾼다는 의미가 아니라 2와 3 위치를 바꾼다는 뜻입니다.)

한 번 이들을 연산해볼까요?

$f = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$ , $g=\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$ 이라고 해보겠습니다.

$f*g$ (편의상 우리가 알고 있는 합성 기호를 *로 쓰겠습니다.)

그렇다면 f*g는 g를 한 번 거치고 f를 거쳐서 변환시키는 방법이 되겠군요.

바꿔봅시다. $f*g(1) = 3\;,f*g(2) = 2\;,f*g(3) = 1$ 네요.

즉 $f*g = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$ 입니다.

우리는 모든 바꿀 수 있는 경우들을 모아놓았기 때문에 어떤 방법들을 합성하든지 저 6가지 방법 중 한 가지 방법이 될 것임을 떠올려볼 수 있습니다.

이는 Group의 특징인데요. 자신의 연산에 의해 닫혀있습니다.
'Closure under operation'
group의 중요한 특성입니다.

또한 어떤 연산에 대해서도 역연산이 존재합니다.

예를 들어 $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}$ 의 역연산은,
3이 있는 곳을 1, 1이 있는 곳을 2, 2가 있는 곳을 3으로 만들어야 하므로
$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$ 을 합성해주면 원래 모양으로 돌아갑니다.

마지막으로 $\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$ 은 어디에 연산을 해주더라도 같은 형태가 나오도록 계산결과를 만듭니다.

저 위의 permutation만 보더라도 group의 연산은 우리가 알고 있는 단순 더하기, 곱하기가 아닙니다.

위의 예시를 토대로 우리는 group의 정의에 대해 알아봅시다.

Definition of groups

A group G is a set equipped with an operation * satisfying the following properties.
1.a,b∈G ⇒ $a\ast b∈G$ (Closure)
2.For a,b,c∈G, $a\ast (b\ast c) = (a\ast b)\ast c$ (Associativity)
3.∃e∈G s.t $a\ast e=a=e\ast a$ for all a∈G.
such e is called the identity element.
4.For any a∈G,∃d s.t $a\ast d$ = e = $d\ast a$ .
such d is called the inverse of a

4가지 정의에 대해 차근차근 알아보죠.

첫번째 정의는 Closure입니다. 너무 당연하게도 성립해야하죠. 만약 연산을 한 결과가 집합을 벗어난다면 수학적으로 별로 할 수 있는 얘기가 없겠습니다.

두번째 정의는 Associativity입니다. 우리가 평소에 잘 알고 있는 결합법칙입니다. 연산의 방향성만 맞다면 어떤 것부터 하던 큰 문제가 생기지 않겠습니다.

세번째 정의는 identity의 존재성입니다. identity도 ring에서 우리가 자주 다뤄왔습니다. identity란 어떤 방향에서 group의 원소에 연산을 하더라도 그 결과가 변치 않게 하는 원소입니다. 그리고 나중에 증명하겠으나 이 identity는 유일합니다.

네번째 정의는 inverse의 존재성입니다. 모든 원소는 inverse가 존재해야합니다. 어떤 a의 inverse는 a에 연산해서 identity가 되는 원소입니다.

Examples

symmetric group
앞서 설명한 것처럼 permutation들의 집합은 group입니다. 만약 위치를 바꾸는 원소가 유한하다면 즉 T = {1,2,3,...,n} 우리는 그 group을 우리는 symmetric group이라고 부릅니다.

위에서 Associativity만 보이지 않았는데 이는 매우 직관적으로 보이므로 패스하겠습니다.

2.dihedral group $D_n$
dihedral group은 n각형의 대칭관계에 대한 group입니다.

한 번 살펴보죠.
dihedral group은 n각형의 각 꼭짓점에 수를 대응하고 회전변환과 대칭변환으로 만들 수 있는 n각형의 숫자 배치에 관한 그 함수를 원소입니다. 말이 어려우니 예시로 확인하겠습니다.

우리는 그 예시로 $D_4$ , 즉 사각형을 생각해보겠습니다.
숫자는 다음과 같은 방식으로 대응시킬 수 있습니다.

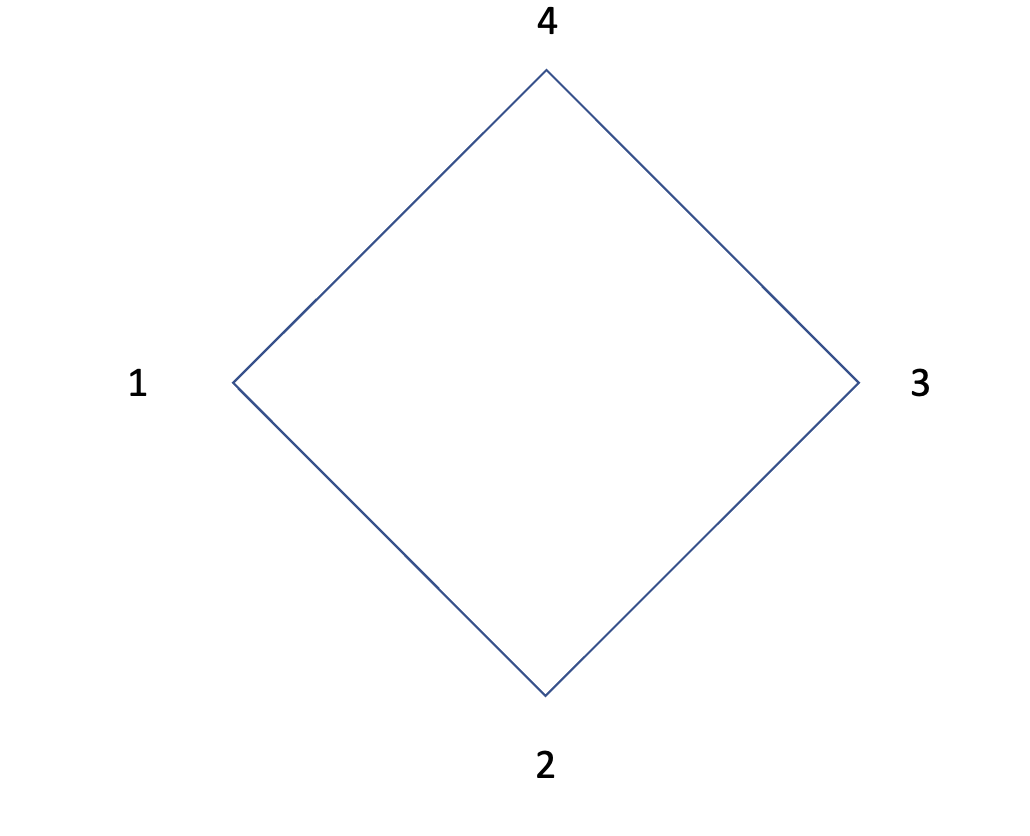
이 숫자를 대응시키는 방식으로 우리는 8가지의 원소가 존재한다는 사실을 떠올릴 수 있습니다.
다음과 같이 말입니다.

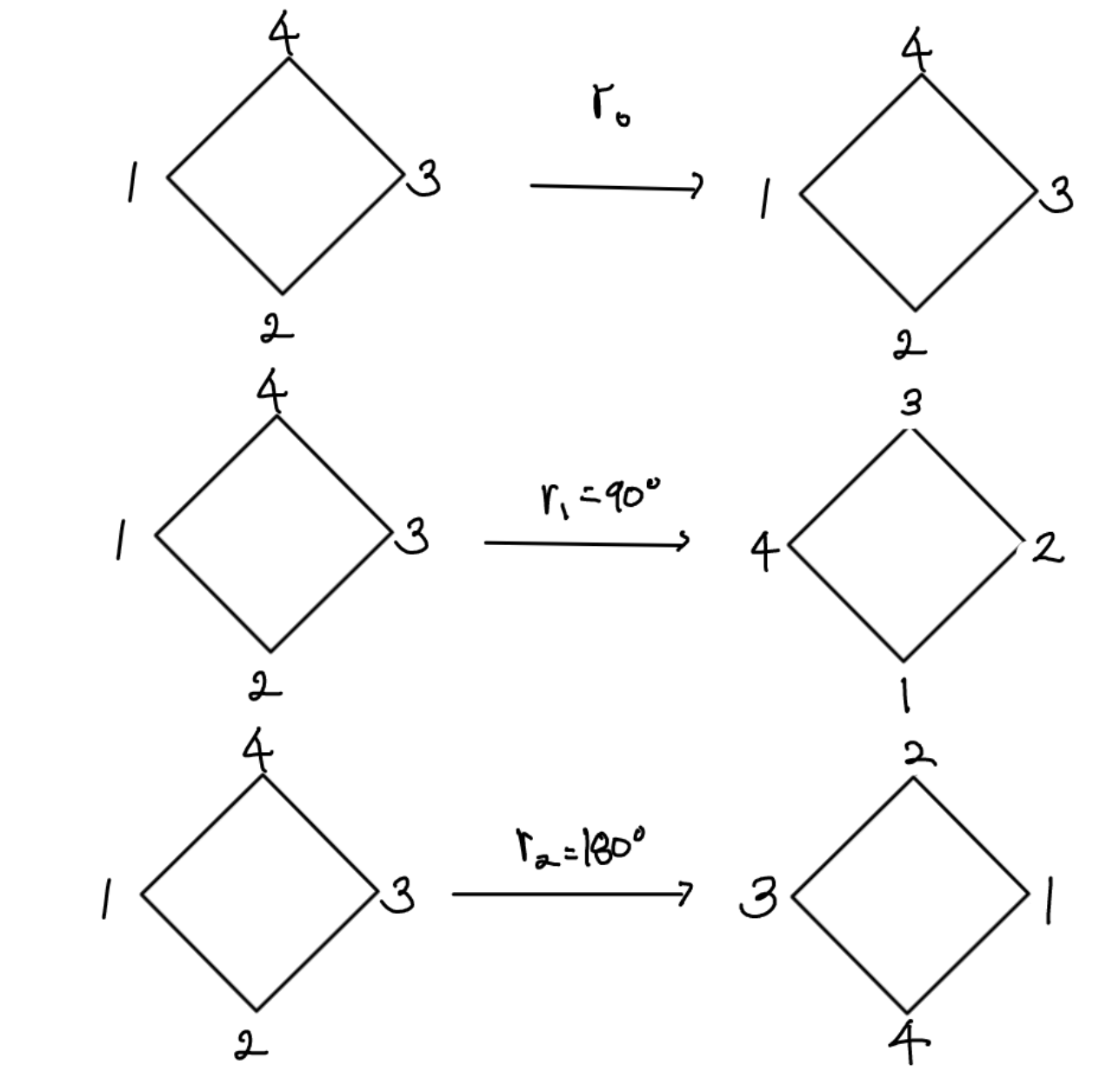
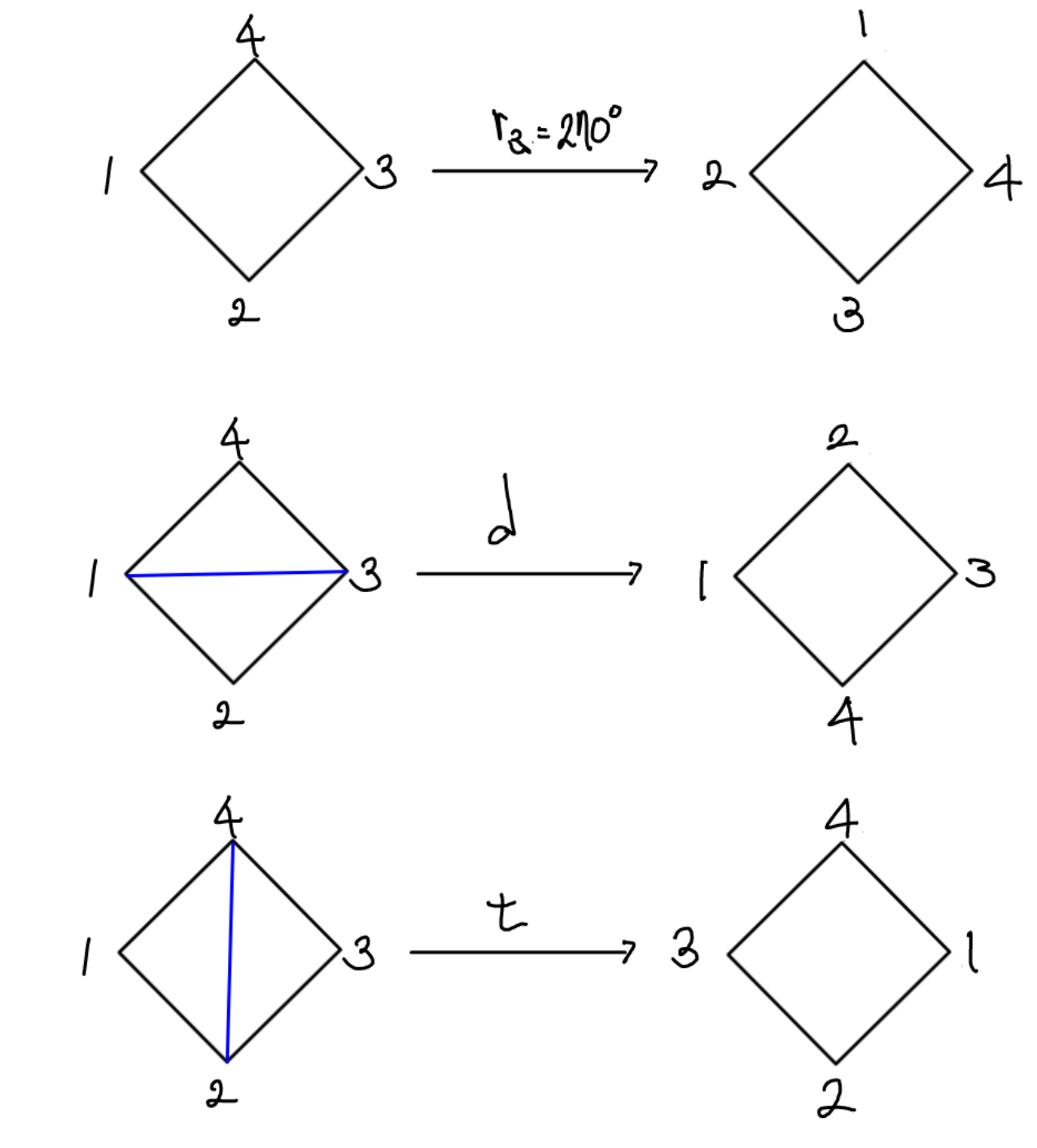
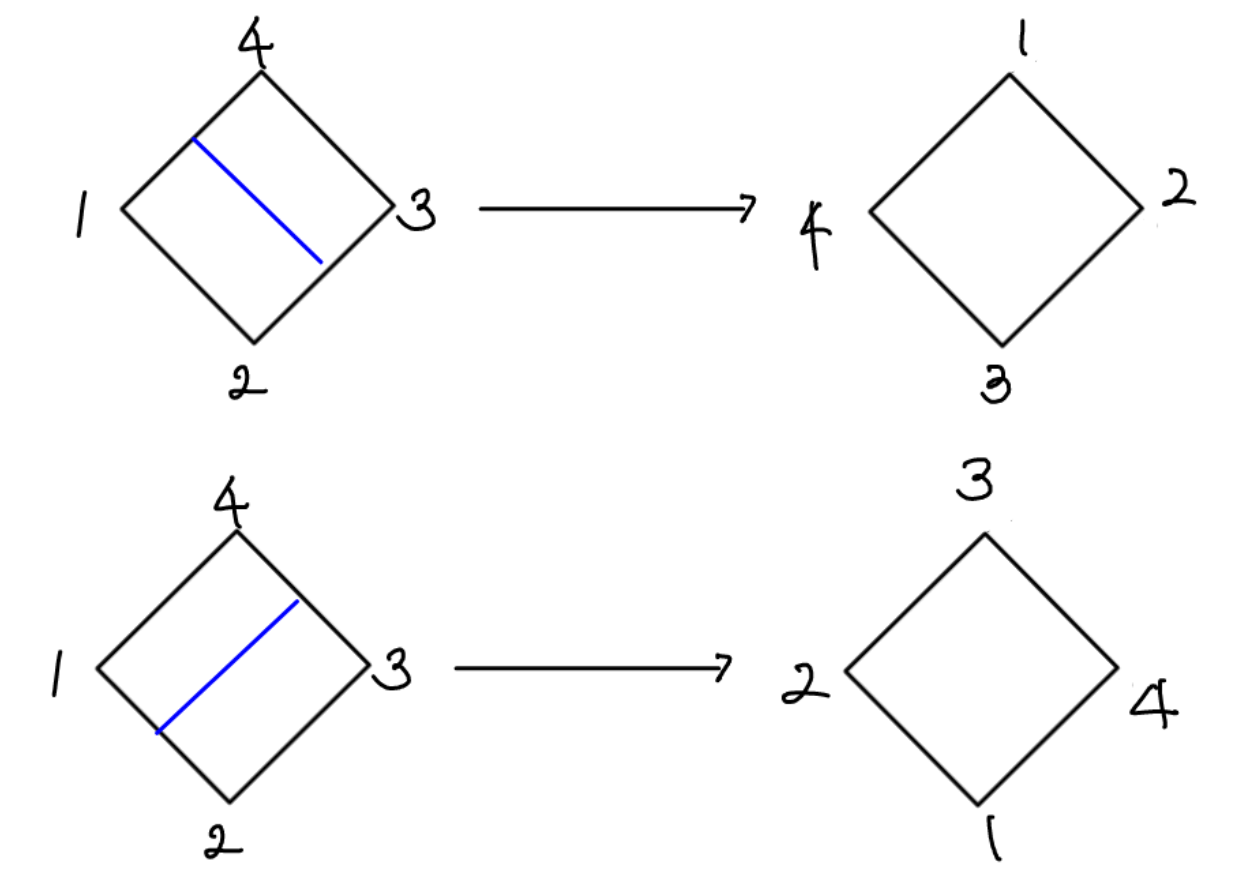
이 변환들을 다 모아놓은 집합 $D_4$ = { $r_0,r_1,r_2,r_3,d,h,t,v$ }
(그림에서는 누락되었는데 마지막 두 개의 변환이 각각 v, h입니다.)

여기서 identity는 $r_0$ 입니다. 그도 그럴 것이 자기자신의 형태를 반환하기 때문이죠.

여타 다른 변환들은 각각의 inverse가 있습니다. 돌린 방향의 역으로 바꾸어주는 연산을 실행하면 됩니다.
예를 들어 d,t,v,h 연산의 역은 각각 자신을 다시 수행하는 것이 역일 것입니다.

def of abelian

우리는 이 군론에 지대한 영향을 끼친 위대한 수학자 Abel의 이름을 따 abelian이라는 표현을 씁니다. 이 abelian은 우리가 원래 알고 있던 commutative와 같은 의미입니다.

A group(G, $\ast$ ) is called abelian if $a\ast b = b\ast a$ ∀a,b∈G

abelian이라는 것은 즉, 연산의 순서를 잘 바꿀 수 있다는 의미이고 매우 강력한 조건입니다.

Thm7.1 Ring을 Group으로 만들기

Let (R,+, $\cdot$ ) be a ring. Then (R,+) js an abelian group.

Ring은 원래 2가지 연산을 들고 있습니다. +와 *이죠. 그런데 이 중에서 +연산만 가져온다면 이 Ring은 Group이 됩니다. 신기하죠? 그런데 어찌보면 당연합니다.

0을 identity로 택하고, 그러면 ring의 정의에 따라 inverse 즉, $a$ 를 0으로 만드는 $-a$ 가 잘 존재하고, associativity는 ring이므로 잘 성립하고, +니까 closure under addition이고. 끝.
심지어

그런데 *는 잘 안되요우. 왜냐? 일단 0의 inverse가 없고, field가 아닌 이상 0이 아닌 원소에서 inverse가 잘 존재하지는 않기 때문.

Thm7.1의 예시로는 알고 있는 모든 ring이 다 가능합니둥.

Thm7.2

Let (F,+, $\cdot$ ) be a field. Then (F $\setminus$ { $0_F$ }, $\cdot$ ) is an abelian group.

*에서 안되는 이유를 위에 적어놓았습니다.

그런데 그를 해결한 것이 다음 Thm7.2입니다.
field에서 0을 제외했으니 각각에 깔끔하게 inverse 존재하구요, 1이 identity로 존재합니다. 또한 field는 commutative이므로 자연스럽게 abelian이고 associativity 당연하며 closure under multiple이니 깔끔하게 group 땅땅땅.

앞으로 Notation : $F^\ast = F\setminus{0_F}$ 입니다.

example로는
$ℚ^\ast,ℝ^\ast$ 뭐 다 됩니다.
그런데 $ℤ^\ast$ 는 안됩니다. 애초에 ℤ가 field가 아닙니다.

Thm 7.3

(R,+ $\cdot$ ) : ring with identity, U : set of units in R
Then (U, $\cdot$ ) is a group.

어떤 ring에서 unit만 모아놓아도 group이 됩니다. 어차피 unit은 0이 아니거든요.

example

R = ℤ. U = {1,-1}
U만 가져오고 곱하기 가져오면 group이 잘 됩니다.
R = $ℤ_8$
Recall that a∈ $ℤ_n$ is a unit ⇔ (a,n)=1
U = {1,3,5,7}
그러면 곱하기를 가져왔을 때 U가 group입니다.
R = $M_2(ℝ)$ = { $\begin{pmatrix} a & b \\ c & d \end{pmatrix}|a,b,c,d∈ℝ$ }
ad-bc ≠ 0 인 모든 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 을 모으면 inverse가 있으니까 unit이고 group이 잘 되겠습니다.