Abstract

문법 오류 수정(GEC)를 위한 시스템 조합을 간단한 이진 분류로 공식화
간단한 로지스틱 회귀 알고리즘이 GEC 모델을 결합하는 데 매우 효과적
CoNLL-2014 tast에서 가장 높은 기본 GEC 시스템의 F0.5 점수를 4.2점 BEA-2019 test에서 7.2점 증가
기존 앙상블보다 더 높은 F0.5 점수로 더 나은 보정을 생성

1. Introduction

일반적으로 최근의 SOTA 시스템은 일반적으로 사전 학습된 대규모 masked language model을 사용하는 sequence tagging 방식과 합성 데이터로 Transformer 아키텍처를 사전 학습하는 sequence-to-sequence 방식으로 구분
합성 데이터 생성 방법과 사용되는 seed 말뭉치의 차이는 GEC 시스템을 더욱 다양하게 함

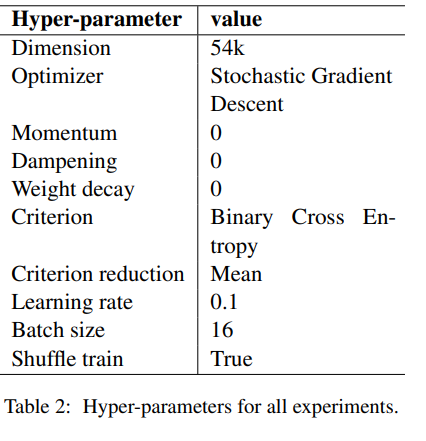
이러한 차이로 인해 모델마다 장단점이 있다 (그림 1)
GEC 모델의 강점 차이를 시스템 조합 방법을 통해 결합하여 더 나은 문법 오류 보정을 생성하는데 활용
본 논문에서는 CoNLL-2014, BEA-2019 shared task 모두에서 SOTA
본 논문의 기여

• 우린 각각의 edit을 독립적으로 예측하는 이진 분류로 공식화하여 문법 오류 수정 시스템을 결합
• 제안된 방법은 기본 시스템의 출력에만 의존하므로 모든 기본 GEC 시스템과 호환

2. Related Work

한 접근법(MEMT)는 어떠한 edit type 유형에 의존하지 않고 출력 문장만 사용하는 반면, 다른 두 접근법(IBM, GEC-IP)는 edit type만 사용하고 어떤 가설(구성 시스템의 출력 문장)은 전혀 사용하지 않음
이 섹션에서는 시스템 조합 방법을 보완하는 또 다른 시스템 조합 방법(DDC)으로 기본 시스템에 다양성을 도입

2.1 MEMT

MEMT는 여러 개의 시스템으로부터 기계 번역 가설을 결합하도록 설계된 시스템 결합 방법
MEMT는 먼저 가설을 정렬하고 후보 토큰들의 모든 가능한 경로를 생성함으로써 가설들을 결합
MEMT는 가능한 후보 토큰을 검색하는 데 no repetition, weak monotonicity, completeness 등 몇 가지 제약 조건이 있음
그런 다음 n-gram 언어 모델 점수, 가설과의 n-gram 유사도 및 후보 내 토큰 수에 따라 후보 토큰의 점수를 매기는 방법을 학습

2.2 IBM

IBM 시스템 조합 방법은 두 가설의 편짐을 첫 번째 가설에만 나타나는 편집, 두 가설에 모두 나타나는 편집, 두 번째 가설에만 나타나는 편집 세가지 그룹으로 구분하여 작동
모델은 각 편집 유형에 대해 어던 그룹을 포함할지 결정
IBM 방식은 한 번에 두 시스템만 결합할 수 있음
따라서 두 개 이상의 시스템을 결합하려면 이 방법을 반복적으로 적용해야 함

2.3 GEC-IP

GEC-IP는 IBM 방법과 유사하지만 더 간단하며, IBM 방식에서 사용되는 것처럼 실수 값 매개변수를 최적화하고 나중에 반올림하는 대신 비선형 정수 프로그래밍을 사용하여 매개변수를 직접 최적화
GEC-IP와 IBM의 또 다른 주요 차이점은 한번에 두 개의 시스템만 결합하는 대신 여러 개의 기본 시스템을 결합할 수 있음
GEC-IP에선 각 편집 유형에 대해 시스템은 최종 수정으로 적용할 하나의 기본 시스템의 편집만 선택하고 다른 기본 시스템의 편집은 무시

2.4 DDC

다양성 중심 조합(DDC)는 결합 시스템의 성능을 향상시키기 위해 시스템 결합 시나리오에서 기본 시스템 간의 다양성을 증가시키는 것을 목표로 하는 방법
기본 시스템이 다양하고(거의 상관 없음) 유사한 품질을 가져야 한다는 것을 보여줌
DDC는 미게 조정을 위해 백본 시스템 역할을 해야 하기 때문에 완전히 블랙박스 방식은 아님
DDC는 강화 학습을 사용하여 기본 시스템에 다양성을 유도한 다음 기성 시스템 조합 방법을 사용하여 기본 시스템을 결합
블랙박스 시스템 조합 방식이 아니라서 본 논문에선 DDC와 비교X

3. Method

이 섹션에선 작업을 공식화하는 방법을 설명하고 가설(즉, 개별 기본 시스템의 출력 문장)에서 가능한 모든 편집을 수집하고 각 편집에 대해 결합된 시스템의 최종 출력 문장을 생성하기 위해 유지해야 하는 지 또는 폐기해야 하는지를 예측하는 방법을 제시
이 방법을 ESC(Edit-based System Combination)라고 부름

3.1 Task Formulation

GEC 시스템 조합을 이진 분류 작업으로 공식화
기본 GEC 모델을 블랙박스로 간주하고 제안된 편집을 기반으로 모델을 결합
기본 GEC 모델에 의해 생성된 가설에서(시작 인덱스, 끝 인덱스, 수정 문자열) 튜플 형태의 편집을 추출. 또한 각 편집에는 자동 오류 주석 도구에서 가져온 편집 유형이 있으며, 편집 유형은 편집 기능의 일부로 사용
각 편집은 삽입(누락의 경우 M), 삭제(불필요: U), 대체(대체의 경우 R) 세 가지 작업 중 하나가 될 수 있음
추출된 편집 유형의 예는 표 1

모든 가설에서 편집된 내용을 조합하여 통합 집합 E로 수집
이 방법은 주변 편집 내용이나 문맥 단어의 정보 없이 각 편집 내용을 독립적으로 평가
편집 유형에 전적으로 의존하며 편집의 텍스트 정보를 사용X
일반화된 선형 모델을 사용하여 다음 하위 섹션에서 정의할 편집의 특징에 따라 결합 시스템의 출력 문장을 생성하기 위해 E의 각 편집을 유지해야 하는지 또는 폐기해야 하는지 예측

3.2 Features

결합할 k 기본(구성 요소) 시스템의 가설이 k개 있다고 가정
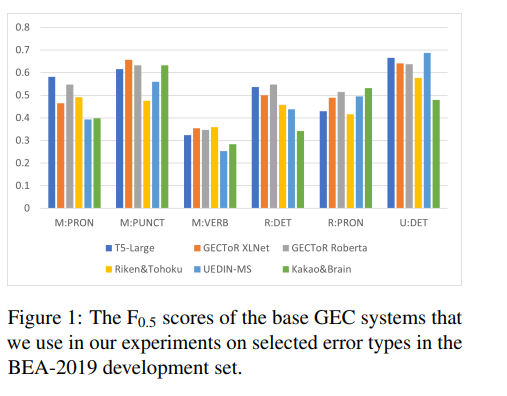
E의 각 편집 e는 feature vector $x_i, i=1...k$를 연결하여 형성되는 feature vector $x$로 표현

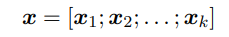
$x_i$는 가설 $i$에 편집 유형이 존재할 경우 가설 $i$의 편집 유형 $e$의 one-hot representation(예: M:ADJ -> [1,0,0,..], M:ADV->[0,1,0,...])이고, 존재하지 않을 경우 0 vector이다

이러한 방식으로 모델은 편집 유형과 어떤 가설이 편집을 제안하는 기준으로 편집을 유지할지 여부를 결정하는 방법을 학습
모델에 제공된 정보는 IBM 방법과 GEC-IP 방법과 동일하나, 작업 공식화 및 최적화 방법은 다름
편집 유형 $T$ 집합의 경우 $x_i ∈ R^{|T|}$ and $x ∈ R^{k|T|}$. 우리 작업에선 $|T|=54$

3.3 Model

로지스틱 회귀를 분류 모델로 사용
로지스틱 회귀를 분류기로 사용하면 적은 양의 학습 데이터로도 모델을 학습할 수 있고 결과를 해석할 수 있음
또한 다양한 종류의 기본 GEC 시스템을 결합할 때 매우 잘 작동한다는 사실을 발견
각 편집에 대해 다음과 같이 출력 문장을 생성하는 데 사용할 올바른 편집일 확률을 얻음:

σ 는 sigmoid function

3.4 Post-processing

여러 가설에서 편집한 내용을 결합하기 떄문에 같은 위치에 여러 번 삽입되거나 중복된 대체로 인해 편집이 중복될 수 있다.

• Multiple insertions
  동일한 위치에서 충돌하는 여러 삽입 편집은 서로 다른 GEC 시스템에 의해 제안된 경우 함께 적용되어서는 안됨
  동일한 위치에 여러 개의 삽입 편집이 있을 경우 (예: (3,3, on), (3, 3, in)) 이를 다중 삽입 충돌로 간주

• overlapping substitutions
  편집의 시작 또는 끝 인덱스가 다른 편집의 시작 및 끝 인덱스 사이에 있는 경우 (예; (2, 4, eaten), (2, 3, ate)), 이를 중복 대체 충돌로 간주

모델에서 확률을 얻은 후 편집을 선택하기 위해 greedy 전략을 사용
먼저, 특정 임계값 이상의 확률을 가진 편집만 고려
그런 다음 확률이 가장 높은 순서부터 가장 낮은 순서로 편집을 정렬하고 편집을 하나씩 확인하여 이전에 선택한 편집과 충돌하지 않는 편집만 선택

4. Experiments

4.1 Implementation

ERRANT를 사용하여 기본 GEC 모델의 출력에서 편집을 추출하고 Pytorch의 선형 모듈을 사용하여 모델을 구현. binary cross entropy가 있는 SGD를 사용하여 모델을 최적화하고 0.5의 임계값을 사용하여 편집을 선택.