[알고리즘] 정렬(sorting) - 힙 정렬(Heap Sort)

이정은·2021년 9월 28일

algorithm

🔨 먼저 힙(Heap)이란?

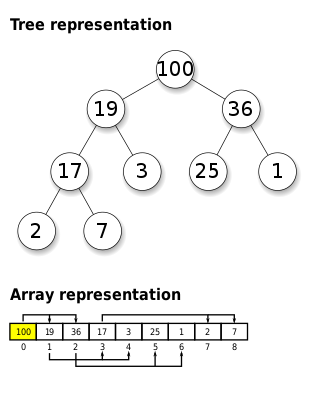
최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위하여 고안된 완전 이진 트리를 기본으로 한 자료구조
- 최대 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 크다.
- 최소 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 작다.
  키 값의 대소관계는 오로지 부모와 자식 관계에서만!! 형제사이에서는 안정해져있다 !

👉 이번 과정에서는 최대 힙을 이용한 내림차순 정렬을 알아보려고 한다

🔨 힙 정렬

최대 힙 트리 or 최소 힙 트리를 구성하여 정렬 하는 방법
내림 차순 정렬을 위해서는 최대힙을 구성, 오름차순 정렬을 위해서는 최소 힙을 구성

👉 과정

<내림차순의 경우>

n개의 자료들로 최대 힙을 만든다.
힙에서 root의 자료(최대값)를 꺼내서 배열의 뒤로 저장한다.
다시 힙 정렬 (그 다음 최대값이 root로 정렬됨)
위의 과정 반복 하면 감소되는 순서로 배열에 저장된다

👉 최대 힙(Max Heap) 구현 (삽입식 힙)

힙 구현시 연결리스트과 배열을 이용하여 구현 할 수 있다.
이번 과정에서는 배열을 이용한 순차 힙에 대해 다루겠다.

1. 최대 힙(max heap) 삽입

새로운 요소가 들어왔을 때, 가장 마지막 노드에 이이서 삽입한다.

힙 순서 속성 복구 ( 부모 노드들과 교환해서 제자리를 찾는다)

int H[101]; // 전역 변수 H배열
int n; // 전역 변수 요소 개수

void insertItem(int key) {
	n++;
	H[n] = key; // 마지막 노드에 삽입
	upHeap(n);
	printf("0\n");
}

//힙 순서 복구 (부모와 비교하여 교환)
void upHeap(int idx) {
	int parent = idx / 2; 
	int tmp;
	if (H[parent] < H[idx] && parent >=1) {
		tmp = H[parent];
		H[parent] = H[idx];
		H[idx] = tmp;
		upHeap(parent);
	}
	return;
}

2. 최대 힙(max heap) 삭제

루트 노드(최댓값) 삭제

삭제된 루트 노드에 힙의 마지막 노드를 가져온다

힙 순서 속성 복구 (자식 노드들과 비교해서 제자리를 찾는다)

int H[101]; // 전역 변수 H배열
int n; // 전역 변수 요소 개수

int removeMax() {
	int key = H[1];
	H[1] = H[n--];
	downHeap(1);
	return key;
}
void downHeap(int idx) {
	int left = idx * 2;
	int right = idx * 2 + 1;
	int tmp;

	if (left <= n) {
		if (right <= n) {
			if (H[left] > H[right]) {
				if (H[idx] < H[left]) {
					tmp = H[idx];
					H[idx] = H[left];
					H[left] = tmp;
					downHeap(left);
				}
			}
			else {
				if (H[idx] < H[right]) {
					tmp = H[idx];
					H[idx] = H[right];
					H[right] = tmp;
					downHeap(right);
				}
			}
		}
		else {
			if (H[idx] < H[left]) {
				tmp = H[idx];
				H[idx] = H[left];
				H[left] = tmp;
			}
		}
	}
	else return;
}