[알고리즘] 정렬(sorting) - 합병 정렬(Merge Sort)

🔨 먼저 분할정복(divide and conquer)이란?

• 분할, 정복, 결합으로 문제를 2개의 작은 문제로 분할하고 각각을 해결한 다음 , 결과를 모아 원래의 문제를 해결하는 방법이다.
• 합병 정렬과 퀵 정렬이 해당된다.

🔨 합병 정렬

• 분할 정복 알고리즘의 하나로 힙 정렬처럼 비교에 기초한 정렬이며 O(nlog n)시간에 수행한다.
• 외부의 우선순위 큐를 사용하지 않고, 데이터를 순차적 방식으로 접근한다.

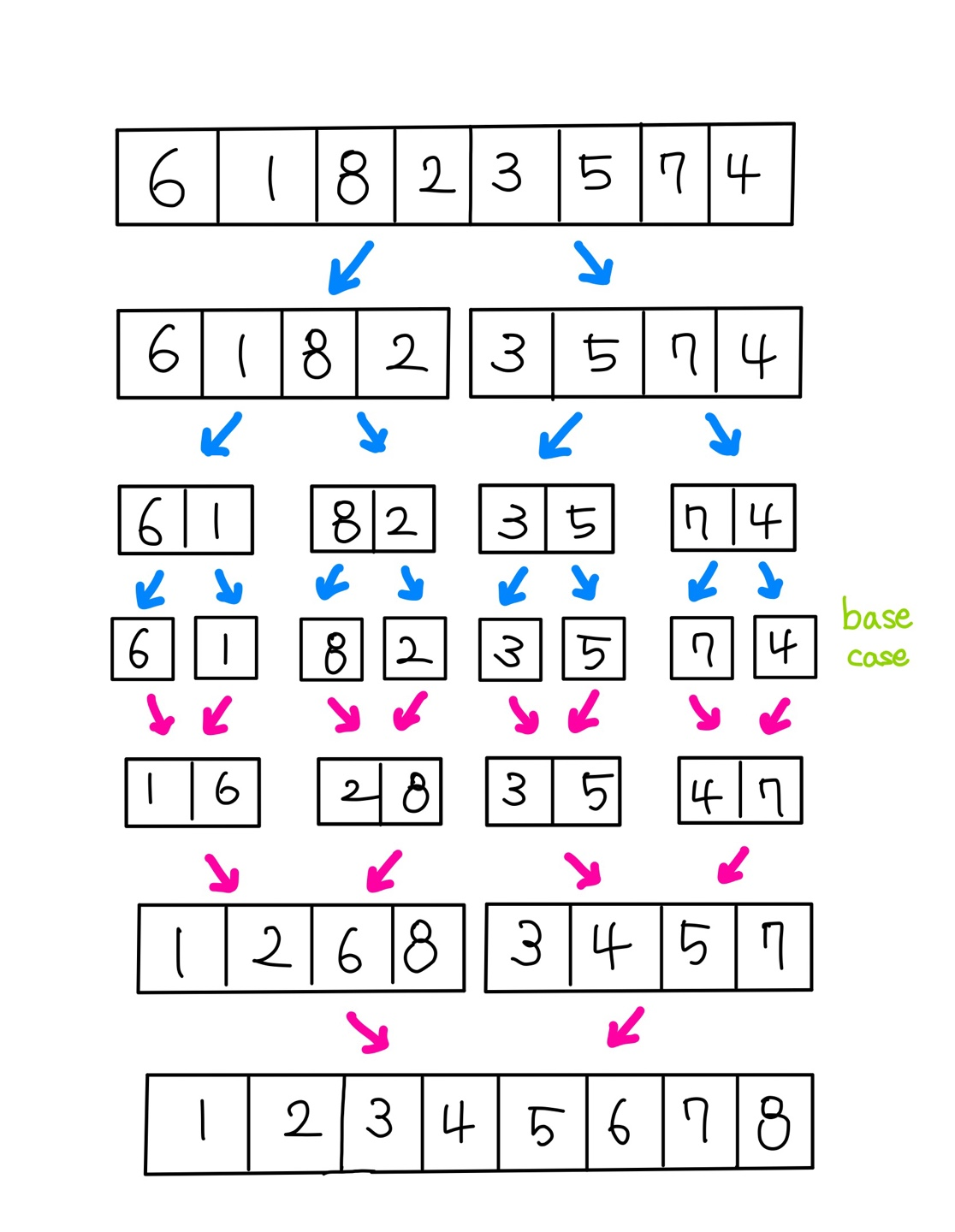
👉 과정

1. 리스트의 길이가 1인 경우 이미 정렬된 것으로 본다. (재귀의 base case)
2. base case가 아닌경우 리스트를 절반으로 비슷한 크기의 두개의 리스트로 나눈다.
3. 두개로 나뉜 리스트들을 또 각각 재귀적으로 합병 정렬을 이용해 정렬해 준다.
4. 두개로 나뉜 리스트들을 다시 하나의 정렬된 리스트로 결합해준다.
   

👉 코드 (단일 연결리스트 이용)

mergeSort()

linkedList* mergeSort(linkedList* li) {
	linkedList* L1 = li;
	linkedList* L2;
   
	if (L1->num == 1) return L1;
	int k = (L1->num) / 2;

	L2 = partition(L1, k);
	L1 = mergeSort(L1);
	L2 = mergeSort(L2);

	return merge(L1, L2);
}
linkedList * partition(linkedList* L, int k) {
	linkedList* re = init();
	node* temp = L->Header;
	re->num = L->num - k;
	L->num = k;

	while (temp && k > 0) {
		temp = temp->next;
		k--;
	}

	re->Header->next = temp->next;
	temp->next = NULL;

	return re;
} 
linkedList * merge(linkedList* L1, linkedList* L2) {
	node* tmp1 = L1->Header->next;
	node* tmp2 = L2->Header->next;
	linkedList * L = init();
	node* tmp3;
	if (tmp1->key <= tmp2->key) {
		
		L->Header->next = tmp1; 
		tmp1 = tmp1->next;
	}
	else {
		L->Header->next = tmp2;
		tmp2 = tmp2->next;
	}
	tmp3 = L->Header->next;

	while (tmp1 && tmp2) {
		if (tmp1->key <= tmp2->key) {
			tmp3->next = tmp1;
			tmp3 = tmp3->next;
			tmp1 = tmp1->next;
		}
		else {
			tmp3->next = tmp2;
			tmp3 = tmp3->next;
			tmp2 = tmp2->next;
		}		
	}
	while (tmp1) {
		tmp3->next = tmp1;
		tmp3 = tmp3->next;
		tmp1 = tmp1->next;
	}
	while(tmp2) {
		tmp3->next = tmp2;
		tmp3 = tmp3->next;
		tmp2 = tmp2->next;
	}
	L->num = L1->num + L2->num;
	return L;
}

전체 코드

#include <stdio.h>
#include <stdlib.h>

//더미 노드 있는 연결리스트

typedef struct node {
	int key;
	struct node * next;
}node;

typedef struct linkedList {
	struct node* Header;
	int num;
}linkedList;

linkedList * init() {
	linkedList* li = (linkedList*)malloc(sizeof(linkedList));
	li->Header = (node*)malloc(sizeof(node));
	li->Header->next = NULL;
	li->num = 0;
	return li;
}

node* createNode(int key) {
	node* new = (node*)malloc(sizeof(node));
	new->key = key;
	new->next = NULL;
	return new;
}

void addNode(linkedList* li, int key) {
	node* new = createNode(key);
	node* temp = li->Header;

	while (temp->next) {
		temp = temp->next;
	}
	temp->next = new;
	li->num++;
}
void printList(linkedList* li) {
	node* tmp = li->Header->next;

	for (int i = 0; i < li->num; i++) {
		printf(" %d", tmp->key);
		tmp = tmp->next;
	}
	printf("\n");
}
linkedList * merge(linkedList* L1, linkedList* L2) {
	node* tmp1 = L1->Header->next;
	node* tmp2 = L2->Header->next;
	linkedList * L = init();
	node* tmp3;
	if (tmp1->key <= tmp2->key) {		
		L->Header->next = tmp1; 
		tmp1 = tmp1->next;
	}
	else {
		L->Header->next = tmp2;
		tmp2 = tmp2->next;
	}
	tmp3 = L->Header->next;

	while (tmp1 && tmp2) {
		if (tmp1->key <= tmp2->key) {
			tmp3->next = tmp1;
			tmp3 = tmp3->next;
			tmp1 = tmp1->next;
		}
		else {
			tmp3->next = tmp2;
			tmp3 = tmp3->next;
			tmp2 = tmp2->next;
		}		
	}
	while (tmp1) {
		tmp3->next = tmp1;
		tmp3 = tmp3->next;
		tmp1 = tmp1->next;
	}
	while(tmp2) {
		tmp3->next = tmp2;
		tmp3 = tmp3->next;
		tmp2 = tmp2->next;
	}
	L->num = L1->num + L2->num;
	return L;
}

linkedList * partition(linkedList* L, int k) {
	linkedList* re = init();
	node* temp = L->Header;
	re->num = L->num - k;
	L->num = k;

	while (temp && k > 0) {
		temp = temp->next;
		k--;
	}

	re->Header->next = temp->next;
	temp->next = NULL;

	return re;
} 

linkedList* mergeSort(linkedList* li) {
	linkedList* L1 = li;
	linkedList* L2;

	if (L1->num == 1) return L1;
	int k = (L1->num) / 2;

	L2 = partition(L1, k);
	L1 = mergeSort(L1);
	L2 = mergeSort(L2);

	return merge(L1, L2);
}

int main() {
	int n;
	int key;
	linkedList* li = init();

	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &key);
		addNode(li, key);
	}
	li = mergeSort(li);

	printList(li);
}

👉 합병정렬 알고리즘 시간 복잡도

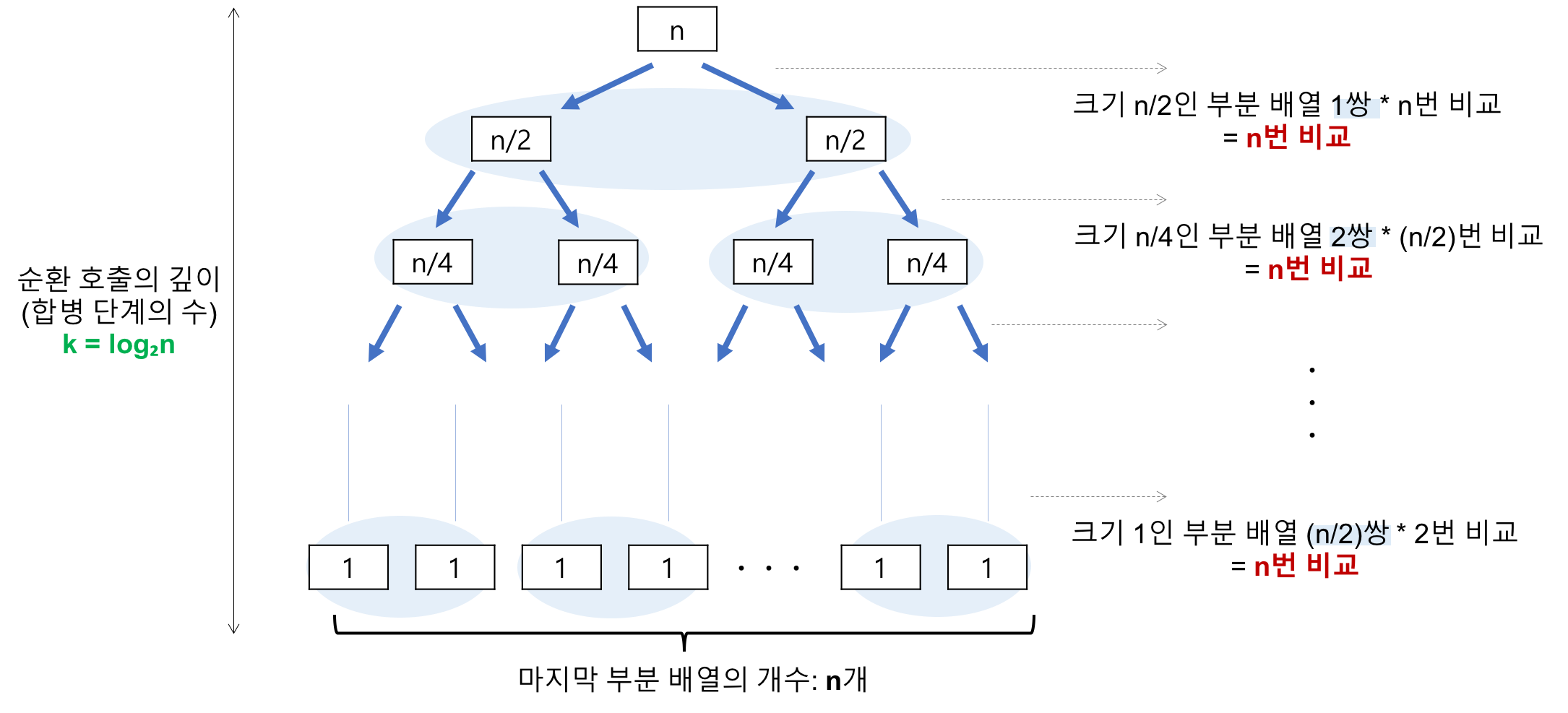
< 시간 복잡도 계산 >

• 분할 단계 : 비교 연산과 이동 연산이 수행 되지 않는다.

• 합병 단계 : 이진 트리로 도식화 할 수 있다. 트리의 높이는 log n 이고 한번의 합병 단계에서는 n번의 비교연산을 한다.
  

• 이동 횟수: 깊이 (log n) * 이동 (2n) (=n개의 요소가 임시배열에 복사 된 뒤 다시 가져오므로) = 2nlog(n)

• T(n) = nlog n(비교) + 2nlog n(이동) = O(nlog n)
  

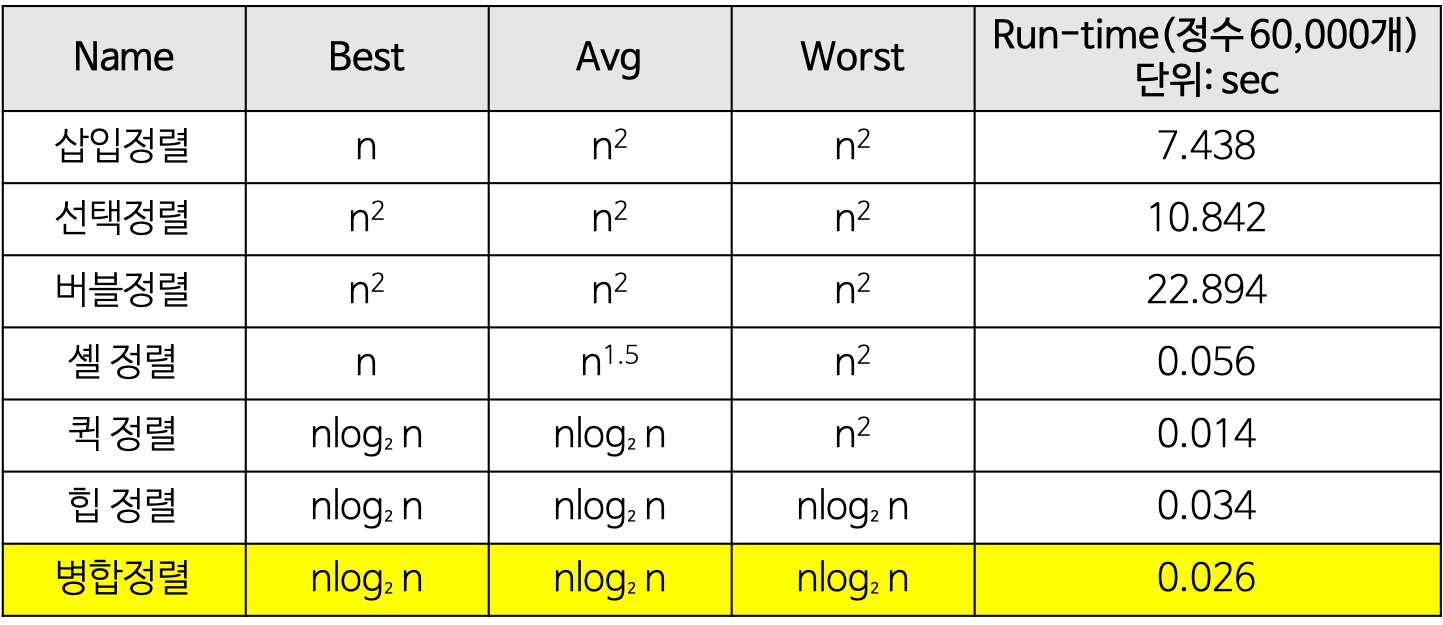
  다음 표를 보면 (퀵정렬,힙정렬, 합병정렬) 은
  다른 정렬에 비해 효율적 이다는 것을 알수있다.

👉 합병정렬 알고리즘 특징

• 장점
  • 안정 정렬 로 중복된 값을 입력 순서와 동일하게 정렬 해준다.
  • 시간 복잡도가 좋은 편 이다.
  • 데이터의 분포의 영향을 덜 받는다.
  • 만일 연결리스트로 구성하면, 링크 인덱스만 변경하면 되므로 제자리 정렬이 가능하다.
• 단점
  • 배열로 정렬시 추가적인 리스트가 필요하다.(제자리정렬이 아니다)
  • 자료가 큰 경우 이동횟수가 많다.

👉 관련된 post

• 선택 정렬(selection sort) : Selection Sort
• 삽입 정렬(insertion sort) : Insertion Sort
• 힙 정렬(heap sort) : Heap Sort
• 합병 정렬(merge sort) : Merge Sort