벡터(Vector)

벡터의 기초

---

스칼라란?

스칼라(Scalar)는 행렬/벡터를 구성하는 요소인 각 숫자들을 의미한다.
스칼라는 행렬/벡터의 구성 요소 중 최소 단위를 의미하며 물리학에서는 크기를 가지는 요소라고 생각된다.

벡터란?

벡터는(Vector)는 스칼라들의 집합으로 표현할 수 있으며, 크기와 방향을 모두 가지는 요소이다.
즉, 벡터는 숫자를 원소로 가지는 배열로써 d차원 공간에서의 원점으로부터의 상대적으로 위치한 한 점을 의미한다. (이 때, d차원은 2차원 이상이며, 1차원의 점은 상수값인 스칼라로 생각한다.)

벡터는 행으로 구성되어있는 행벡터(Row)와 열로 구성되어있는 열벡터(Column)로 나뉜다.

벡터의 연산

---

벡터의 덧셈과 뺄셈

두 벡터의 덧셈/뺄셈의 연산은 같은 모양을 가지는 (차원이 동일한) 벡터끼리의 연산이 가능하다.

두 벡터에의 덧셈은 다른 벡터를 원점으로 두고 상대적으로 위치를 이동하는 것으로 원점을 다른 벡터로 이동하여 상대적 위치를 구하는 연산이된다.

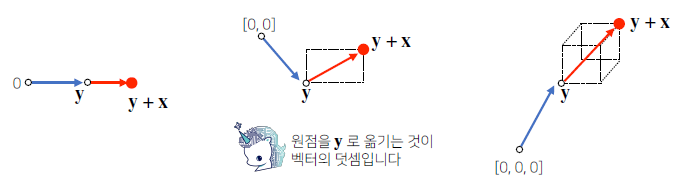
뻴셈은 한 벡터의 방향을 바꾸고 벡터의 덧셈과 같음

벡터의 곱셈

스칼라곱은 벡터의 모든 요소에 $\alpha$만큼의 스칼라를 곱해주는 연산으로 벡터의 길이, 원점으로부터의 상대적 길이를 늘려주는 연산이다. 하지만 스칼라가 음수일 경우에는 벡터의 방향이 변화된다.

두 벡터의 성분곱은 각각에 대응하는 두 벡터의 원소들을 서로 곱하는 연산으로 덧셈/뻴셈과 마찬가지로 두 벡터의 차원이 동일해야 연산이 가능하다.

벡터의 내적

행렬의 기본 연산 중의 하나로, 다른 연산들은 인풋과 아웃풋의 형태가 같지만 내적의 경우 벡터와 벡터의 연산 결괏값이 스칼라로 나오게 되는 연산이다.

두 벡터 $u$와 $v$가 존재할 때, 두 벡터 사이의 각도를 $\theta$라고 할 경우,
$u \cdot v = |u||v|cos\theta$ ($\cdot$은 내적의 연산기호, |u| 와 |v|는 두 벡터 각각의 길이)

내적의 의미

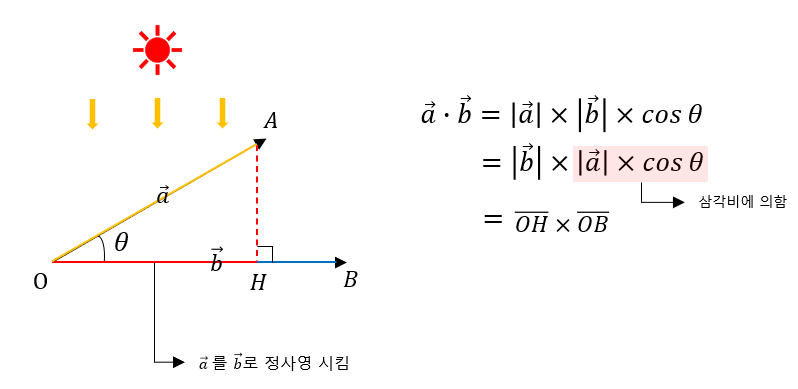
벡터의 내적은 한 벡터를 다른 벡터에 정사영 시킨 길이에 투영된 벡터의 길이를 곱한 것을 의미하며, 이를 통해 두 벡터의 유사도를 구할 수 있다. 내적의 값이 작을 수록 두 벡터의 유사도는 떨어지고, 값이 클 수록 두 벡터의 유사도는 높아진다.

벡터의 길이

---

벡터의 길이(norm)

벡터의 길이(norm)는 원점으로 부터 벡터까지의 거리를 의미한다.
벡터의 길이를 구하는 방식은 $L_1$-norm과 $L_2$-norm 2가지의 방식이 존재한다.

$L_1$-norm: $||X||_1$ = $\sum_{i=1}^{d}|x_i|$ $L_2$-norm: $||X||_2$ = $\sqrt{\sum_{i=1}^d|x_i|^2}$

def l1_norm(x): 
	x_norm = np.abs(x) 
	x_norm = np.sum(x_norm)
	return x_norm

def l2_norm(x): 
	x_norm = x * x 
	x_norm = np.sum(x_norm) 
	x_norm = np.sqrt(x_norm) 
	return x_norm

# L2-norm은 Numpy Module에서 계산을 지원하기 때문에 함수를 구현할 필요가 없다.
from numpy import linalg as la
import numpy as np

x = np.array([89, 34, 56, 87, 90, 23, 45, 12, 65, 78, 9, 34, 12, 11, 2, 65, 78, 82, 28, 78]) 

norm = la.norm(x) 
print('The value of norm is:')
print(norm)
-----------------------------
The value of norm is:
257.48

두 벡터 사이의 거리

서로 다른 두 벡터의 뺄셈에 L1 또는 L2 norm을 씌워주면 거리를 구할 수 있다.$||v1-v2||_1 = ||v2-v1||_1 = \sum_{i=1}^{d}|x_i^{v_1} - x_i^{v_2}|$

$||v1-v2||_1 = ||v2-v1||_1 = \sqrt{\sum_{i=1}^d|x_i^{v_1}-x_i^{v_2}|^2}$

두 벡터 사이의 각도

$L_2$-norm과 벡터의 내적을 활용하여 두 벡터 사이의 각도 $cos\theta$를 구할 수 있다.
($L_1$-norm을 통해서는 구할 수 없다.)

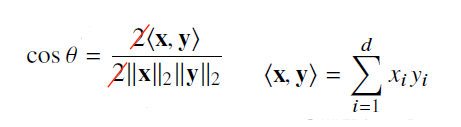
import numpy as np
import linalg from numpy as lin

def angle(v1, v2):
		v = np.inner(v1, v2) / (lin.norm(v1) * lin.norm(v2))
		theta = np.arccos(v)
		return theta

# 프로그래밍으로는 L2-norm을 통해 구하는 것보다 내적으로 구하는 것이 더 편하다.
# np.inner()는 내적을 구하는 method, lin.norm()은 L2-norm을 구하는 method

벡터의 차원

---

벡터 공간과 기저(Bias)

벡터 공간이란 벡터 집합이 존재할 때, 해당 벡터들로 구성할 수 있는 공간을 의미한다. 이 때, 벡터 집합 중에서 벡터 공간을 구성할 수 있는 선형 독립적인 벡터들을 기저(Bias)라고 한다.

벡터 공간 W를 구성하는 벡터 집합을 S라고 할 때, S는 벡터 공간 W를 Span한다고 말하고 W = span(S)로 표현할 수 있다.

• Span의 의미는 벡터 집합S로 벡터 공간 W를 구성할 수 있다는 뜻

전체 벡터 공간 V를 부분 공간 S로 나눌 수 있다. 예를 들어 V가 3차원 공간일 경우에 부분 공간 S는 1차원, 2차원 공간이 될 수 있다.

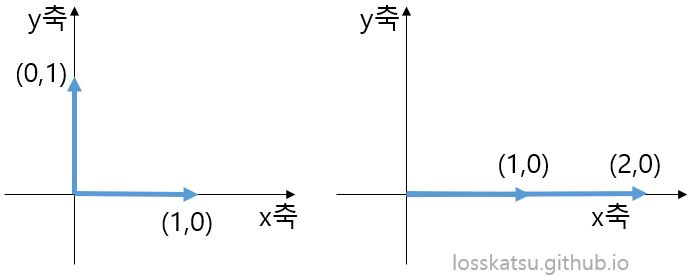
위의 예시 그래프에서 왼쪽 그래프는 (1,0), (0,1) 2개의 벡터가 존재하는데, 해당 벡터는 서로 선형독립적이기 때문에 2차원 벡터 공간의 기저벡터가 된다.

즉, 2차원에 존재하는 모든 벡터는 두 기저 벡터로 표현이 가능해진다.
ex) (2,1) = 2(1,0) + (0,1) (4,3) = 4(1,0) + 3(0,1)

하지만 오른쪽 그래프는 (1,0), (2,0) 2개의 벡터가 존재하지만 두 벡터는 서로 선형독립적이지 않기 때문에 2차원 벡터공간의 기저벡터가 아닌 1차원 벡터공간의 기저벡터가 된다.

선형독립

선형독립이란 하나의 벡터로 다른 벡터를 표현할 수 없는 경우에 두 벡터는 서로 선형독립적이라고 말할 수 있다. 즉, 선형독립이 아닌 경우에는 두 벡터 사이에 선형 관계가 존재하여 상호 의존적이라 다른 벡터를 이용하여 자기 자신을 표현할 수 있다는 의미이다.

고유벡터

---

고유값 고유벡터

정방행렬 A (n x n) 는 임의의 벡터 x (n x 1) 의 방향과 크기를 변화시킬 수 있다. 이를 선형변환이라고 한다. 수많은 벡터 x 중 어떤 벡터들은 A 에 의해 선형 변환되었을 때에도 원래 벡터와 평행한 경우가 있다. 즉, 기존 벡터의 방향은 변하지 않고 길이가 $\lambda$만큼 변했다는 것을 의미한다.
고유벡터란 선형 변환을 취했을 때, 기존 벡터와 평행하게 방향은 유지되면서 크기만 바뀌는 벡터를 의미하고, 고유값이란 고유 벡터가 선형 변환으로 변환되는 ‘크기’ $\lambda$를 의미한다.

• $**Ax = \lambda x$(이 때, $\lambda$는 상수값)**

행렬 A 를 고유값과 고유벡터들로 분해하는 고유값 분해 (eigen decomposition), 정방행렬 뿐만 아닌
m x n 행렬도 분해할 수 있는 특이값 분해 (SVD), 데이터들을 차원 축소시킬 때 가장 원래 의미를 잘 보존시키는 주성분 분석 (PCA) 등에 활용할 수 있으므로 중요하다.