Autoencoder는 무엇을 위해 쓰일까?
여러가지 쓰임새들이 있겠지만 Autoencoder의 가장 중요한 기능중 하나는 Manifold를 학습하는 것이다.
📈 Manifold

Manifold는 복잡한 다차원 구조의 데이터 샘플들을 에러 없이 잘 다루는 subspace 이다.
이런 subspace를 찾으면 별 문제없이 데이터 차원을 축소 할 수 있다.
우리는 항상 원래의 정보를 잘 유지하면서 차원을 축소 하길 바란다.
그러면 이렇게 차원이 축소되었을 때의 장점은 뭘까?
1. Data compression

Auto encoder를 썼더니 JPEG 보다 복원성능이 괜찮더라!!
데이터 크기 자체가 적어지므로 resource들을 아낄 수 있음
2. Data visualization

차원이 낮아지면 시각화를 할 수 있겠지
시각화를 하면 intuition을 얻기 아주 편함
3. Curse of dimensionality
데이터의 차원이 증가할수록 해당 공간의 부피가 기하 급수적으로 증가하기에 데이터의 밀도는 차원이 증가할 수 록 희박해진다 ( 10개중 1개 있던게 3차원이되면 1000개중 한개!) => 차원이 커지면 모델링이 굉장히 힘들고 복잡해지겠지?
차원이 +2 됐을 뿐인데 같은밀도로 데이터를 채워 넣으려면 99개의 데이터가 더필요함 ㄷㄷ
Manifold Hypthesis

- 고차원의 데이터의 밀도는 낮지만 , 이들의 집합을 포함하는 저차원의 매니폴드가 있다.
- probability density 는 급격하게 낮아진다 매니폴드를 벗어나는 순간
매니폴드 가정과 다르게 고차원의 데이터가 Uniform하게 분포되어있다면 (매니폴드가 없고) 무작위로 뽑았을 때 몇번 정도는 유의미한 결과가 나와야 하는데

위와 같은 정보만 계속 뽑힌다. => Manifold hypothesis 합리적인데?
4. Discovering most important feature
중요한 feature들만 쏙쏙 뽑아왔다고 기대 가능

이런식의 Manifold가 있을 것이고, Manifold 좌표들이 조금씩 변할 떄 원 데이터도 유의미하게 조금씩 변화를 보인다.
예를들면
- v1 은 줌과 관련된 factor (feature)
- v2 벡터는 rotation과 관련된 factor

또 의미적으로 가깝다고 생각되지만 고차원 공간에서 두 샘플들간의 유클리드 거리가 먼경우가 굉장히 많다. => 매니폴드를 생각하면 말이 됨


좋은 예시가 있어서 가져와봤다.

manifold가 잘뽑히면 위와같이 Disentangled 된 형태로 나타난다. dominant feature들을 자동으로 잘 찾아서 구분함
PCA
차원축소의 한 예시이다.
pca는 원데이터를 샘플공간에 뿌린뒤 분산이 최대 축이 되는 plain을 찾아서 projection을 시키는 방식이다.

단순히 projection만 하는 process라 고차원에서

이 와 같이 구불구불한 친구는 잘 구분을 못한다. (entangled 되어있다.)
이외에 비선형 차원 축소 기법(LLE, IsoMap 등)은 데이터의 비선형적인 특성을 유지하면서 변환을 수행한다. 이번 포스트에선 다루지 않겠다. (너무 다른곳으로 새는 느낌 ㅠ)
Neighborhood based training 의 한계

차원축소 , Non-parametric Density Estimation (데이터에 따른 확률 분포 모델링) 은 기본적으로 유클리드 거리가 가까운 이웃을 사용한다.
그러나 고차원 데이터 간의 유클리디안 거리는 유의미한 거리 개념이 아닐 가능성이 높다. (아까 언급했듯이)
이웃이 진짜 이웃이 아니다! (이웃사람임 ㅋㅋ)
Auto-Encoder
오토인코더는 Neighborhood problem에서 탈피함
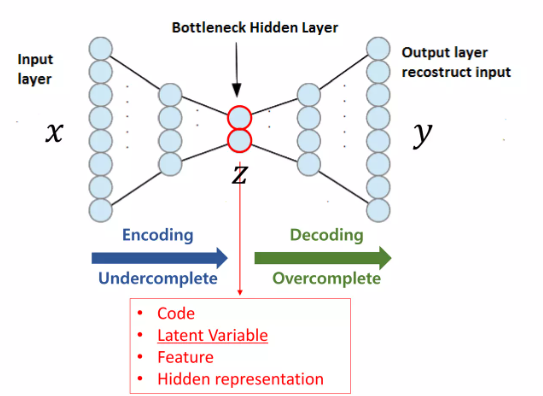
처음 부터 이런형태는 아니였다고 한다.
앤드류 Ng 이 중간 차원이 오히려 늘어나는
sparse-auto-encoder 라는걸 엄청 밀었다고 함 ㅋㅋ( 지금은 안씀)

Autoencoder는 비지도 학습으로 이루어지던 차원 축소의 패러다임에서 self-supervised 학습이라는 새로운 방식을 제안했습니다=> 각광을 받음.
Encoder 관점에서 train loss가 최적화 되면서 적어도 학습데이터는 잘 latent vector로 표현할 수 있게 된다.
Decoder 관점에서 최소한 학습데이터는 생성해 낼 수 있게 된다. (minimmum 성능 보장 <=> GAN)

activation function을 거치지 않는 Linear Auto-encoder라는 것도 있다.
Stacking Auto-encoder
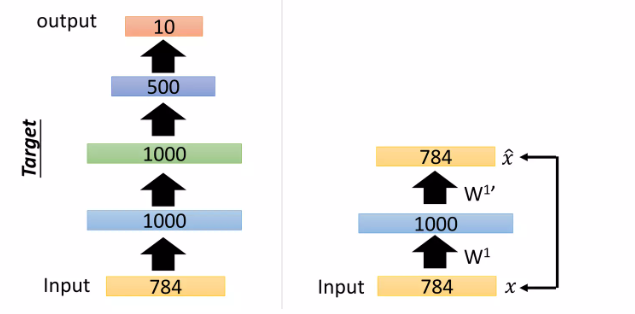
1. auto-encoder 하나 학습시키고 디코더부분의 W1'를 저장해둠

2. 두번째 오토인코더를 학습시킴 (input은 전에 학습시킨 오토인코더의 latent space) 마찬가지로 W2'저장해둠

3. 반복 (W3'저장) => 반복 (W4'저장)

- 디코더 부분: W4' W3' W1' W2' 차례 대로 forward 해서 784 출력
Denoising auto-encoder
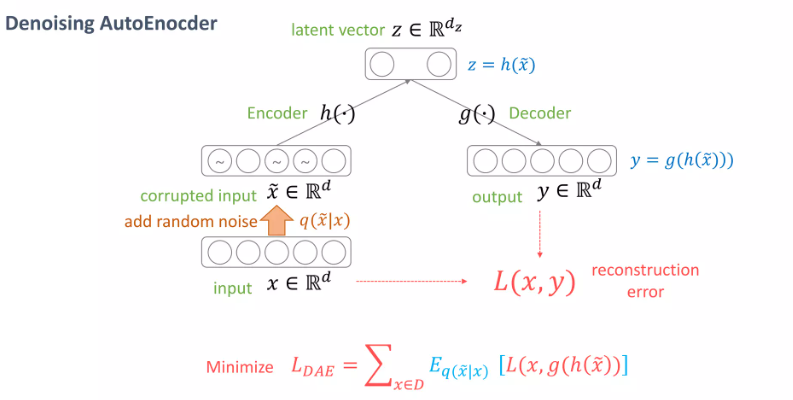
야~김철수 와 야~김철수 + 차소리는 같은 dominant feature를 공유 => 같은 매니폴드에 있어야 하지 않을까?(의미적으론 같지만 원 데이터 공간상에선 다른)
노이즈를 넣어도 노이즈 넣기 전의 정보가 나오도록 오토인코더를 학습시키자!

DAE 성능 좋더라~~

노이즈를 더 추가해서 학습시켰더니? edge detect를 더 잘한 모습도 보여줌 😲


stacked-auto-encoder에도 추가해봤더니 에러가 잘 줄어듬

각 레이어 마다 베르누이 샘플링을 적용하였더니 역시 SDAE는 노이즈에 robust한 모습을 보여주었다.
예제 설명: 레이어에 베르누이 샘플링 적용
기본 개념
- 베르누이 샘플링: 각 값이 0 또는 1이 될 확률이 있는 샘플링 방법입니다. 예를 들어, 80% 확률로 1, 20% 확률로 0이 되는 베르누이 분포를 사용할 수 있습니다.
과정
입력 데이터
- 예를 들어,
[1, 0, 1, 1, 0]이라는 입력 데이터가 있다고 가정합시다.첫 번째 인코딩 레이어
- 입력 데이터를 첫 번째 인코딩 레이어를 통해 변환합니다. 예를 들어, 이 레이어에서
[0.8, 0.1, 0.7, 0.9, 0.2]라는 출력이 나왔다고 합시다.베르누이 샘플링 적용
- 이제 이 출력 값을 베르누이 샘플링을 통해 새로운 값으로 변환합니다.
- 각 출력 값에 대해 특정 확률로 샘플링합니다. 예를 들어,
[0.8, 0.1, 0.7, 0.9, 0.2]에 대해 0.5 이상의 값은 1로, 그 이하의 값은 0으로 변환한다고 가정합니다.- 결과는
[1, 0, 1, 1, 0]가 될 수 있습니다.다음 레이어로 전달
- 베르누이 샘플링을 통해 변환된 값
[1, 0, 1, 1, 0]는 다음 인코딩 레이어의 입력으로 사용됩니다.- 이 과정을 통해 각 레이어에서 샘플링을 반복적으로 적용합니다.
실제 예제
예를 들어, 손글씨 숫자 '3'의 이미지가 있습니다. 이를 첫 번째 레이어에 입력하면, 다음과 같은 출력이 나올 수 있습니다:
- 출력:
[0.8, 0.3, 0.9, 0.2, 0.7]이 출력에 대해 베르누이 샘플링을 적용하면:
- 샘플링 결과:
[1, 0, 1, 0, 1]이 결과는 다음 레이어의 입력으로 사용됩니다. 이 과정을 거치면서 각 레이어에서 샘플링을 통해 노이즈를 제거하거나 특성을 강화하게 됩니다.
요약
베르누이 샘플링을 각 레이어에 적용하는 것은, 각 레이어의 출력을 확률적으로 0 또는 1로 변환하는 과정을 의미합니다. 이를 통해 디노이징 오토인코더는 노이즈가 섞인 입력에서도 중요한 특징을 효과적으로 학습하고 복원할 수 있게 됩니다.
본 블로그 포스트는 이활석님의 오토인코더의 모든 것동영상 강의를 참조했음을 밝힙니다.
