- "가까운 이웃에게 물어봐"
- 회귀로도, 분류로도 사용 가능
정리
알고리즘의 원리, 개념
- 거리를 계싼하여 가장 가까운 k개 이웃의 y값들의 평균으로 예측/분류 한다
전제조건
성능
- 하이퍼파라미터에 의해 성능이 달라진다.
- k값: 클수록 단순(최대치가 되면 평균 모델이 되니까), 작을수록 복잡
- 거리계산법: 유클리드? 맨하탄?
원리
- 예측할 데이터(x_val)와 주어진 데이터(x_train)의 모든 거리를 계산한다.
- 가장 짧은 거리, 즉 예측할 데이터와 가장 가까운 데이터(x_train)를 k개 찾는다.
- 찾은 k개의 y값의 평균을 계산하여 예측한다.
k값 결정
- 동점을 만들지 않기 위하여 k는 홀수를 사용한다.
- 보통 데이터 수의 제곱근 근처에서 찾는다.
- k가 1이면?
- k가 최대값이면?
- k의 최댓값 = train 개수
- 평균 모델이 된다.
특징
장점
- 분포의 모양에 구애 받지 않는다
- 설명변수의 개수가 많아도 상관 없다
단점
- 느리다
- 훈련데이터를 모델에 함께 저장하기 때문에 모델 사이즈가 커진다.
- fit 할때 훈련데이터가 저장되고, predict 하는 순간 거리를 계산한다
- 모델 해석이 어렵다
전처리: Scaling
- 값의 범위가 큰 feature 일 수록 거리 계산에 영향을 많이 주며, 더 중요한 변수로 여겨질 수 있다. 따라서 값의 범위를 맞춰주는게 중요하다.
Normalization
- 0~1 사이로 바꿔줌
fit_transform: train 데이터에 대해 fit(min, max 찾기) + transform(계산해라, 값들을 그것으로 변환해라)transform: val 데이터에 대해 계산만 해라. 즉 적용만 해라.
Standardization
KNN 회귀 - 모델링 절차
0. 데이터 준비
import numpy as np
import pandas as pd
데이터 분할: x, y 나누기
target = 'medv'
x = data.drop(target, axis=1)
y = data.loc[:, target]
NaN 조치
가변수화
데이터 분할: train, validation 나누기
x_train, x_val, y_train, y_val = train_test_split(x, y, test_size = .3, random_state = 2022)
Scaling
- KNN은 스케일링 필수!
- MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x_train_s1 = scaler.fit_transform(x_train)
x_val_s1 = scaler.transform(x_val)
from sklearn.preprocessing import StandardScaler
scaler2 = StandardScaler()
x_train_s2 = scaler2.fit_transform(x_train)
x_val_s2 = scaler2.transform(x_val)
1. 함수 불러오기
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import *
2. 선언(모델 설계)
- 하이퍼파라미터 조절
n_neighbors: K값metric: 거리계산법: 유클리디안, 맨하탄
model = KNeighborsRegressor(n_neighbors = 10, metric = 'euclidean')
3. 학습(모델링)
model.fit(x_train_s1, y_train)
4. 검증: 예측
pred = model.predict(x_val_s1)
5. 검증: 평가
mean_squared_error(y_val, pred, squared = False)
mean_absolute_error(y_val, pred)
mape = mean_absolute_percentage_error(y_val, pred)
1 - mape
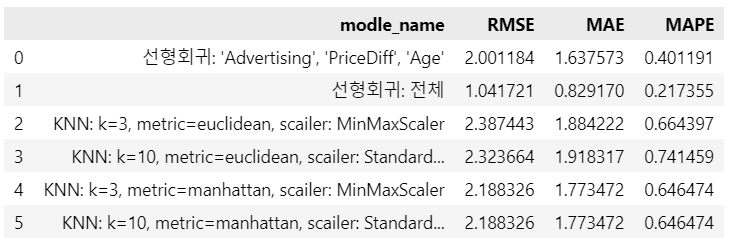
선형회귀 vs KNN
- 예시임..
- 결론, 그때그때 다르다! 해봐야 안다!
rmse, mae, mape = [], [], []
pred = [pred1, pred2, pred3, pred4, pred5, pred6]
modle_name = ["선형회귀: 'Advertising', 'PriceDiff', 'Age'", "선형회귀: 전체",
'KNN: k=3, metric=euclidean, scailer: MinMaxScaler',
'KNN: k=10, metric=euclidean, scailer: StandardScaler',
'KNN: k=3, metric=manhattan, scailer: MinMaxScaler',
'KNN: k=10, metric=manhattan, scailer: StandardScaler']
for i, p in enumerate(pred):
model_no.append(i+1)
rmse.append(mean_squared_error(y_val, p, squared = False))
mae.append(mean_absolute_error(y_val, p))
mape.append(mean_absolute_percentage_error(y_val, p))
result = pd.DataFrame({'modle_name': modle_name, 'RMSE': rmse, 'MAE': mae, 'MAPE': mape})
result
KNN: 분류-모델링 절차

