- CNN이 무엇일까?
-
CNN(Convolutional Neural Networks):
딥러닝에서 주로 이미지나 영상 데이터를 처리할 때 쓰이며, 이름에서 알수있다시피 Convolution(합성곱)이라는 전처리 작업이 들어가는 Neural Network 모델입니다. -
Convolution?(합성곱) 이란?
CNN에서 합성곱은 특징을 추출하는 중요한 연산이다.
CNN에서 합성곱 연산은 보통 다음과 같은 형태로 이루어진다.
입력 데이터(예: 이미지) 위를 커널(필터) 이 이동하며 필터와 입력 데이터의 대응되는 값들을 곱한 후 더하여 각 영역의 특징을 추출한다.
출력 값 = ∑(입력 값 × 필터 값)
필터 크기(예: 3×3, 5×5)와 스트라이드(stride, 이동 거리)에 따라 결과가 달라짐.
1D 합성곱: 오디오 신호에서 특정 패턴을 찾는 과정.
2D 합성곱: 이미지, 단백질 시퀀스에서 엣지(edge), 선(line) 등의 특징을 감지하는 과정.
3D 합성곱: 동영상 데이터에서 시간축까지 포함하여 특징을 추출하는 과정. -
그렇다면 왜 CNN이라는 방법을 쓰기 시작했을까요?
이에 대한 답은 일반 DNN(Deep Neural Network)의 문제점에서부터 출발합니다. 일반 DNN은 기본적으로 1차원 형태의 데이터를 사용합니다. 때문에 (예를들면 1028x1028같은 2차원 형태의)이미지가 입력값이 되는 경우, 이것을 flatten시켜서 한줄 데이터로 만들어야 하는데
이 과정에서 이미지의 공간적/지역적 정보(spatial/topological information)가 손실되게 됩니다.
ex)
원래 이미지에서 가까운 픽셀들이 가지는 공간적 관계(Spatial Relationship)가 사라짐.
예를 들어, 고양이 사진에서 귀와 눈이 서로 가까이 위치해야 의미가 있는데, Flatten하면 픽셀들의 순서가 의미 없는 1차원 벡터가 되어버림.
즉, 위치 정보(Topological Information)가 손실되면서, 이미지의 구조적인 특징을 제대로 학습하기 어려워짐.
또한 추상화과정 없이 바로 연산과정으로 넘어가 버리기 때문에 학습시간과 능률의 효율성이 저하됩니다.
ex)
CNN과의 차이
CNN은 Conv Layer(합성곱 계층)을 이용해 이미지에서 작은 특징부터 점진적으로 추출하는 추상화 과정(Feature Extraction 단계)을 거쳐.
처음에는 엣지(Edge), 코너(Corner) 같은 저수준 특징을 찾고,
점점 더 복잡한 형태(예: 눈, 코, 귀)로 발전하면서 고수준 의미(Semantic Feature)를 학습하게 됨.
하지만 일반 DNN은 이런 추상화 과정 없이 처음부터 모든 픽셀을 연결하여 처리하기 때문에:
모든 뉴런이 모든 뉴런과 연결 → 파라미터 수 증가 → 학습 속도 느려짐(학습시간의 저하)
특징이 추출되지 않음 → 모델이 이미지의 의미를 학습하는 데 비효율적(능률의 효율성 저하)
CNN이 이미지를 보고 먼저 중요한 특징을 찾아서 요약한 후 판단하는 반면, DNN은 처음부터 모든 픽셀을 보면서 판단해야 하니까 시간이 오래 걸리는 거야.
이러한 문제점에서부터 고안한 해결책이 CNN입니다. CNN은 이미지를 날것(raw input) 그대로 받음으로써 공간적/지역적 정보를 유지한 채 특성(feature)들의 계층을 빌드업합니다. CNN의 중요 포인트는 이미지 전체보다는 부분을 보는 것, 그리고 이미지의 한 픽셀과 주변 픽셀들의 연관성을 살리는 것입니다.
- 왜 CNN을 쓰는지 조금 더 쉽게 예를 들어 봅시다.

예를 들어 우리는 어떠한 이미지가 주어졌을때 이것이 새의 이미지인지 아닌지 결정할 수 있는 모델을 만들고 싶다고 가정합시다. 그렇다면 새의 주요 특징인 새의 부리가 중요한 포인트가 될 수 있습니다. 때문에 모델이 주어진 이미지에 새의 부리가 있는지 없는지 판가름 하는것이 중요 척도가 될 것입니다. 하지만 새의 전체 이미지에서 새의 부리 부분은 비교적 작은 부분입니다. 때문에 모델이 전체 이미지를 보는 것 보다는 새의 부리 부분을 잘라 보는게 더 효율적이겠죠? 그것을 해주는것이 CNN입니다. CNN의 뉴런이 패턴(이 경우에서는 새의 부리)을 파악하기 위해서 전체 이미지를 모두 다 볼 필요가 없습니다.
CNN이 "전체를 보지 않는다"는 의미
CNN이 전체 이미지를 "한 번에" 보는 것이 아니라, 작은 부분(로컬 영역)을 보면서 패턴을 학습한다는 뜻이야.
즉, 모델이 한 번에 전체 픽셀을 다 연결해서 학습하는 것이 아니라, 작은 영역을 순차적으로 보면서 중요한 특징을 찾는다는 거야.
예를 들어:
일반 DNN은 이미지의 모든 픽셀을 FC Layer에 입력 → 각 픽셀 간 공간적 관계를 무시
CNN은 작은 필터(커널)를 사용해 지역적인 특징을 학습 → 점진적으로 더 큰 특징을 학습
이런 방식을 사용하면, 이미지를 효과적으로 분석할 수 있고, 학습해야 할 가중치 수도 크게 줄어들어 연산량이 최적화됨.
필터를 Stride에 따라 전체에 적용하는 이유
CNN의 필터(커널)는 특정 패턴(예: 새의 부리, 눈, 날개 등)을 찾는 역할을 해. 하지만 이미지에서 그 패턴이 어디에 위치할지는 미리 알 수 없잖아?
필터를 전체에 적용하는 이유
-
특징이 어디에 있을지 모르기 때문
새의 부리는 이미지의 중앙에 있을 수도 있고, 왼쪽 위에 있을 수도 있어.
따라서 CNN은 한 곳만 보는 게 아니라, 여러 위치에서 같은 필터를 적용하면서 특징이 어디에 있는지 찾아야 해.
같은 필터를 다른 위치에도 적용하는 것이 CNN의 핵심 개념이야! (이를 가중치 공유(Weight Sharing)라고 해) -
부분적인 정보를 통합하여 전체적인 의미를 파악하기 위해
필터는 한 번에 한 영역만 보지만, 이 과정을 여러 번 반복하면 전체 이미지를 커버할 수 있어.
이렇게 하면 지역적 특징(부리, 눈, 날개 등)을 먼저 찾고, 이후 계층(layer)을 거치면서 점점 더 큰 의미를 이해할 수 있어. -
효율적인 연산을 위해
필터를 한 번만 적용하면, 특정 위치에서만 특징을 감지할 수 있지만, 이렇게 하면 위치가 달라지면 학습한 특징을 다시 학습해야 하는 비효율성이 생겨.
따라서 Stride를 조정하면서 여러 영역을 스캔하여 위치에 관계없이 패턴을 찾도록 설계한 거야.
Stride의 역할
Stride(스트라이드)는 필터를 얼마나 많이 이동시키면서 적용할지 결정하는 값이야.
Stride = 1 → 필터를 한 픽셀씩 이동하며 적용 → 더 세밀하게 특징을 학습 (더 많은 연산 필요)
Stride = 2 → 필터를 두 픽셀씩 이동하며 적용 → 연산량 감소, 하지만 조금 더 거친 특징만 학습 가능
Stride를 조절하면, 특징을 잡아내는 해상도와 연산량을 조절 가능
CNN은 전체를 한 번에 보는 것이 아니라, 작은 영역을 스캔하면서 학습한다!
"CNN은 전체 이미지를 볼 필요가 없다"는 말은:
한 번에 모든 픽셀을 다 연결해서 학습하지 않아도 된다는 뜻이고,
작은 필터를 사용하여 지역적인 특징을 찾아낸 후,
그 필터를 전체 이미지에 적용하여 위치에 상관없이 패턴을 찾는다는 의미야.
CNN의 가중치 공유 덕분에, 같은 필터를 여러 위치에서 적용하면 특징의 위치에 관계없이 패턴을 감지할 수 있어.
Stride를 조정하면서 필터를 이동시키는 것은 연산 효율성을 높이고, 다양한 크기의 특징을 감지하기 위한 방법이야!
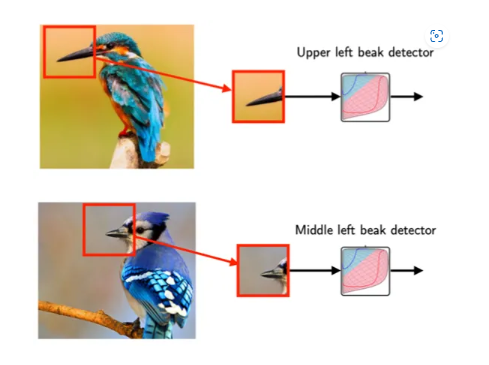
또한 위의 두 이미지를 보면 새의 부리부분이 이미지의 다른 부분에 위치해 있다는 것을 알 수 있습니다. 위의 이미지는 이미지의 새의 부리가 왼쪽 상단에 위치한 반면 아래의 이미지는 상단 가운데 부분에서 약간 왼쪽 부분에 위치. 때문에 전체적인 이미지보다는 이미지의 부분 부분을 캐치하는 것이 중요하고 효율적일 수 있습니다.
- CNN의 주요 컨셉들
- Convolution의 작동 원리
우선 2차원의 이미지를 예로 들어 봅시다. 2차원 이미지는 픽셀 단위로 구성되어 있습니다.

위의 이미지는 손글씨로 쓰여진 ‘8’의 gray scale 이미지 입니다. 자세히 보면 28x28단위의 픽셀로 구성되어 있습니다. 우리는 이 데이터 입력값을 28x28 matrix(행렬)로 표현할 수 있습니다. 즉, 우리는 2차원 이미지를 matrix로 표현할 수 있다는 뜻입니다. 우리가 CNN에 넣어줄 입력값은 이렇게 matrix로 표현된 이미지 입니다.
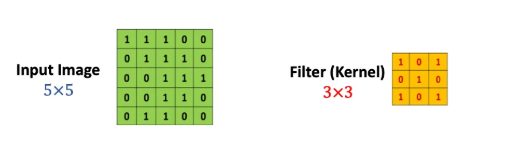
조금 더 간략한 예를 위해 위와 같이 5x5의 matrix로 표현된 이미지 입력값이 있다고 가정합시다. 그리고 CNN에는 필터(커널)가 존재합니다. 위의 예시의 경우에는 3x3크기의 필터입니다. 쉽게 표현하면 이 하나의 필터를 이미지 입력값에 전체적으로 훑어준다고 생각하면 됩니다. 즉 우리의 입력값 이미지의 모든 영역에 같은 필터를 반복 적용해 패턴을 찾아 처리하는 것이 목적입니다. 그렇다면 이미지 위에 이 필터를 훑어줄때 어떤 일이 일어날까요? 정확히 말하면 이 필터를 이용해 연산처리를 해주는 것입니다. 그리고 이 연산처리는 matrix와 matrix간의 Inner Product라는 것을 사용합니다.
- Inner product이란 무엇일까요?
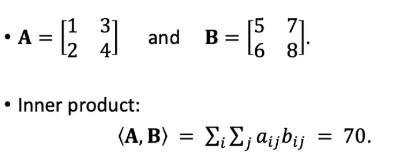
쉽게 말해 같은 크기의 두 matrix를 놓고 각 위치에 있는 숫자를 곱해 모두 더해주는 것입니다.
다시 본론으로 되돌아와서 어떻게 이 이미지 입력값 matrix의 각 부분과 필터가 연산처리 되는지 그림으로 살펴보겠습니다.
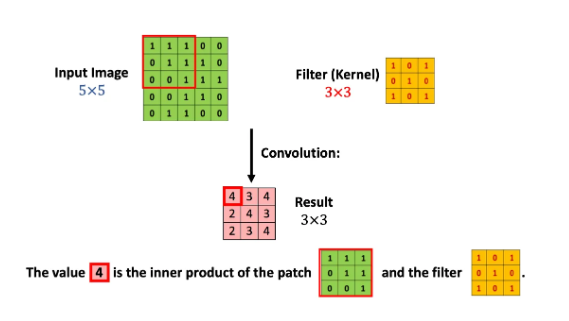
우선 빨간 테두리 부분의 matrix와 필터의 Inner product연산을 해주면 그 결과값은 4가 됩니다. 그리고 필터를 한칸 옆으로 옮겨주면,
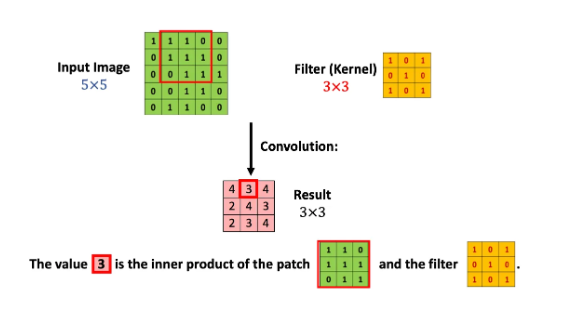
이번엔 이 빨간 테두리 부분의 matrix와 필터의 연산처리를 해주어 결과값 3을 얻어냅니다. 이러한 과정을 전체 이미지 matrix에 필터 matrix를 조금씩 움직이며 반복해 줍니다. 그렇게 반복하여 얻어낸 결과값이 분홍색으로 표시된 matrix입니다.
자세히 보면 결과값의 크기는 3x3이라는 것을 파악할 수 있습니다. 5x5로 구성된 칸들에 3x3크기의 블록을 움직인다고 생각해보면 너비와 높이 둘다 3번씩 놓을 수 있기 때문입니다. 이것을 수학적으로 표현해보면 다음과 같습니다.
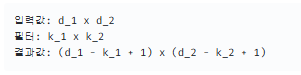
(5 - 3 + 1) * (5 - 3 + 1)
- Zero Padding
방금 우리가 살펴본 Convolution처리를 보면 5x5크기의 이미지에 필터처리를 해주었더니 결과값의 크기가 3x3로 줄어들었다는 것을 알 수 있습니다. 즉 손실되는 부분이 발생한다는 뜻입니다. 이런 문제점을 해결하기 위해 Padding이라는 방법을 사용할 수 있습니다. 쉽게 말해 0로 구성된 테두리를 가공 전 이미지 가장자리에 감싸 준다고 생각하면 됩니다.
그렇다면 위의 경우 5x5크기의 이미지 입력값이 7x7크기 (d_1 + 2) x (d_2 + 2) 가 될 것입니다. 이 상태에서 3x3필터를 적용해줄 경우 똑같이 5x5크기의 결과값을 얻을수 있겠죠? 이렇게 되면 입력값의 크기와 결과값의 크기가 같아졌음, 즉 손실이 없어졌음을 볼 수 있습니다.
Zero Padding을 하는 이유
- 출력 크기를 원래 입력 크기와 동일하게 유지하기 위해 (Same Padding)
기본적으로 CNN의 합성곱 연산(Convolution)을 하면 이미지 크기가 줄어들어.
예를 들어,
5×5 이미지에 3×3 필터를 적용하면 출력 크기는:
(5−3+1)×(5−3+1)=3×3
이렇게 줄어들어. 이걸 계속 반복하면, 네트워크가 깊어질수록 이미지 크기가 급격하게 줄어들어서 정보 손실이 발생하게 돼.
Zero Padding을 사용하여 입력 크기를 늘려주면, 출력 크기를 원래 입력 크기와 같게 유지할 수 있어.
이렇게 하면 초기 크기를 유지하면서 깊이 있는 네트워크에서도 충분한 특징을 추출 가능!
- 가장자리(Edge) 정보를 보존하기 위해
CNN은 특징을 찾는 과정에서 필터를 이동하며 지역적인 정보를 학습해.
하지만 필터가 적용될 때 이미지의 가장자리(Padding이 없는 부분)는 상대적으로 덜 학습될 수 있어.
즉, 중앙 부분은 필터가 여러 번 적용되면서 잘 학습되지만, 가장자리는 한두 번만 적용되기 때문에 특징을 제대로 학습하기 어렵다는 문제가 생겨.
Zero Padding을 사용하면 이미지 가장자리에도 충분한 연산이 적용되어 중요한 특징을 잃지 않게 됨.
- 깊은 네트워크에서 정보 손실을 방지하기 위해
CNN 모델이 깊어지면 계속해서 크기가 줄어들면서 정보가 사라지는 문제가 발생할 수 있어.
예를 들어, 여러 개의 Conv Layer를 거치면 특징 맵 크기가 급격히 작아져버려서 유용한 정보가 다 사라질 수도 있어.
Zero Padding을 적용하면 크기를 유지하면서 더 깊은 네트워크를 만들 수 있음.
따라서 더 많은 층을 쌓아도 중요한 정보가 손실되지 않고 유지됨!
네트워크가 깊어질수록 크기가 너무 작아져서 정보가 손실됨
→ Zero Padding을 사용하면 크기를 유지할 수 있어.
가장자리 부분이 학습이 잘 안 됨
→ Zero Padding을 추가하면 모든 영역을 균형 있게 학습 가능.
더 깊은 네트워크를 만들려면 크기를 유지해야 함
→ 그렇지 않으면 연산할 공간이 너무 작아져버림.
- Stride
Stride는 쉽게 말해 필터를 얼마만큼 움직여 주는가에 대한 것입니다. stride값이 1일경우 필터를 한칸씩 움직여 준다고 생각하면 됩니다(즉, 위의 예시의 경우 stride값이 1일때 입니다). 참고로 stride-1이 기본값이고 stride는 1보다 큰 값이 될 수도 있습니다. stride값이 커질 경우 필터가 이미지를 건너뛰는 칸이 커짐을 의미하므로 결과값 이미지의 크기는 작아짐을 의미합니다. stride값을 적용한 수학적 표현은 다음과 같습니다.
입력값: d_1 x d_2
필터: k_1 x k_2
stride: 1
결과값: (((d_1 - k_1) / s) + 1) x (((d_2 - k_2) / 2) + 1)
- The Order-3 Tensor
지금까지 우리는 2차원 이미지의 입력값을 살펴보았습니다. 물론 입력값이 3차원인 경우도 존재합니다. 예를들면 컬러이미지는 R, G, B의 세가지 채널로 구성되어 있기 때문에 d_1 x d_2 x 3과 같은 삼차원의 크기를 갖습니다. 이러한 모양을 order-3 텐서라고 칭합니다. 유사하게 익숙한 2차원의 이미지는 order-2 텐서(즉 matrix)라고도 칭합니다.
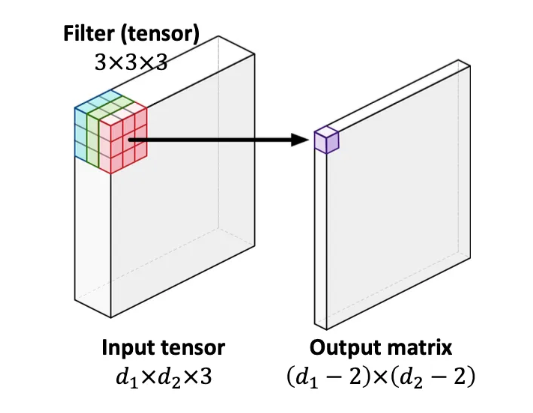
위의 이미지와 같이 이 경우에 필터는 k1xk2x3의 크기를 가진 order-3 텐서가 됩니다. 연산처리는 똑같이 Inner product를 사용합니다. 그러면 당연히 결과값의 모양은 matrix가 되겠죠?
- CNN의 전체적인 네트워크 구조
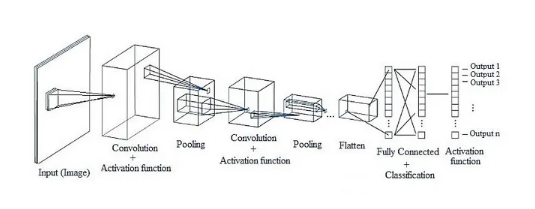
CNN의 구조는 기존의 완전연결계층(Fully-Connected Layer)과는 다르게 구성되어 있습니다. 완전연결계층(또는 Dense Layer이라고도 합니다)에서는 이전 계층의 모든 뉴런과 결합되어있는 Affine계층으로 구현했지만, CNN는 Convolutional Layer과 Pooling Layer들을 활성화 함수 앞뒤에 배치하여 만들어집니다.
- 기존의 완전연결계층(Fully-Connected Layer, Dense Layer)
완전연결계층(FC Layer)는 이전 계층의 모든 뉴런과 연결(Affine 변환)되는 방식이야.
Affine 변환이란?
Affine 변환은 다음과 같은 수식으로 표현돼:
Y=WX+B
X : 입력 데이터 (뉴런의 값)
W : 가중치 (Weight)
B : 편향 (Bias)
Y : 다음 층으로 전달될 값
즉, 모든 입력 뉴런이 모든 출력 뉴런과 연결되며, 행렬 곱 연산을 통해 변환되는 구조야.
- CNN은 완전연결계층과 다르게 작동함
CNN은 "모든 뉴런을 연결하는 대신, 지역적 특징을 학습하도록 설계"되었어.
완전연결층과 CNN의 차이점
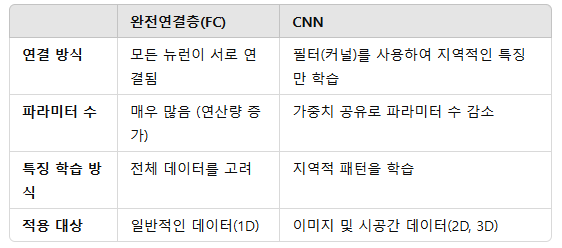
- CNN의 기본 구조
CNN은 다음과 같은 주요 계층으로 구성돼:
Convolutional Layer (합성곱 계층)
작은 필터(커널)를 사용하여 지역적인 특징을 추출.
Affine 변환(완전연결) 없이 입력 이미지의 공간적 관계(Spatial Information)를 유지하면서 학습.
Pooling Layer (풀링 계층)
특징을 축소하고, 가장 중요한 정보만 추출.
대표적으로 Max Pooling(최댓값 풀링)과 Average Pooling(평균 풀링)이 있음.
크기를 줄여 연산량을 감소시키고, 과적합 방지 효과.
Activation Function (활성화 함수)
ReLU 함수 등을 사용하여 비선형성을 추가하고, 특징을 더 잘 구분할 수 있도록 함.
Convolution Layer 뒤에 배치됨.
Fully-Connected Layer (완전연결층, Dense Layer)
마지막 단계에서 분류(예: 고양이 vs 개)를 수행하기 위해 사용.
하지만 CNN은 초반부터 완전연결층을 쓰지 않고, 주로 마지막 단계에서만 사용.
- 왜 CNN은 Convolutional Layer + Pooling Layer를 사용하는가?
이미지의 공간적 정보(Spatial Information)를 유지하기 위해
→ 완전연결층은 이미지를 1D 벡터로 변환하므로 공간 정보를 잃음.
→ CNN의 합성곱 연산(Convolution)은 지역적 패턴을 학습하여 공간적 구조를 유지할 수 있음.
연산량을 줄이고, 효율적으로 학습하기 위해
→ 완전연결층은 뉴런 개수가 많아질수록 연산량이 급격히 증가함.
→ CNN은 필터를 공유(Weight Sharing)하여 연산량을 줄이고 일반화 성능을 높임.
더 깊은 네트워크를 만들 수 있도록 하기 위해
→ CNN 구조에서는 Conv Layer + Pooling Layer를 반복해서 쌓을 수 있음.
→ 이를 통해 점진적으로 저수준 특징(엣지, 색깔 등) → 고수준 특징(눈, 입, 형태 등)으로 발전함.
- 결론
기존의 완전연결층(FC Layer)은 모든 뉴런이 서로 연결(Affine 변환)되지만, CNN은 지역적인 특징을 학습하는 구조
CNN은 Convolutional Layer(합성곱 계층)와 Pooling Layer(풀링 계층)를 쌓아서 중요한 특징을 점진적으로 학습함
CNN의 장점: 공간적 정보를 유지하고, 연산량을 줄이며, 더 깊은 네트워크를 구성할 수 있음
즉, CNN은 모든 뉴런을 연결하지 않아도 중요한 특징을 자동으로 학습하는 구조라는 것
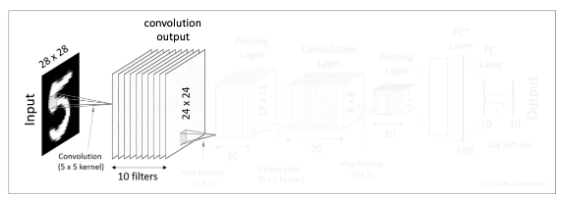
첫번째 Convolutional Layer
우선 우리에게 주어진 입력값은 28x28크기를 가진 이미지입니다. 이 이미지를 대상으로 여러개의 필터(커널)을 사용하여 결과값(feature mapping이라고도 합니다)을 얻습니다. 즉 한개의 28x28 이미지 입력값에 10개의 5x5필터를 사용하여 10의 24x24 matrics, 즉 convolution 결과값을 만들어 냈습니다. 그 후 이렇게 도출해낸 결과값에 Activation function(예를 들면 ReLU function)을 적용합니다. 이렇게 첫번째 Convolutional Layer이 완성되었습니다. 우리는 여기서 한 Convolutional Layer는 Convolution처리와 Activation function으로 구성되어 있다는 것을 알 수 있습니다.
A Convolutional Layer = convolution + activation
왜 필터를 여러 개(10개) 사용하는가?
CNN에서 필터(커널)는 이미지의 특징을 추출하는 역할을 해.
즉, 다양한 필터를 사용하면 서로 다른 특징을 학습할 수 있기 때문에 여러 개를 사용하는 거야!
- 필터가 하는 역할
각각의 필터는 이미지에서 특정한 패턴(Feature)을 감지해.
예를 들어:
어떤 필터는 수평선(Horizontal Edge)을 감지
어떤 필터는 수직선(Vertical Edge)을 감지
어떤 필터는 곡선(Curvature)을 감지
어떤 필터는 특정 텍스처(Texture)를 감지
즉, 필터 하나만 사용하면 특정한 패턴 하나만 학습할 수 있어서, 이미지의 전체적인 특징을 파악하는 데 한계가 있어.
그래서 여러 개의 필터를 사용해서 다양한 특징을 추출하는 거야!
CNN의 필터가 학습하는 특징을 우리가 알 수 있을까?
CNN이 충분한 에포크(Epoch)를 거쳐 학습이 끝난 후, 각 필터가 정확히 어떤 특징을 감지하는지 우리가 직접 알 수 있을까?
정답은 "어느 정도는 알 수 있지만, 필터가 학습한 특징을 사람이 직접 해석하는 것은 제한적이다."
컴퓨터는 필터가 어떤 특징을 감지하는지 스스로 학습하지만,
우리는 CNN이 학습한 필터를 시각화하는 방법(Visualization Techniques)을 사용하여 어느 정도 분석할 수 있어!
CNN의 필터가 어떤 특징을 학습하는지 직접 볼 수 있는 방법
CNN에서 필터는 데이터를 학습하면서 특정한 패턴을 감지하도록 최적화됨.
이때, 우리가 필터가 학습한 패턴을 이해하는 방법은 크게 3가지야!
- 필터 시각화 (Filter Visualization)
CNN의 각 필터가 어떤 패턴을 감지하는지 직접 확인할 수 있음.
학습이 끝난 필터(커널)를 시각적으로 출력하면, 어떤 필터가 어떤 특징을 학습했는지 알 수 있음.
예제:
초기층(첫 번째 Conv Layer)
가장 단순한 패턴을 감지 (예: 엣지, 선, 밝기 차이 등)
중간층(중간 Conv Layers)
곡선, 텍스처, 단순한 형태를 감지
깊은 층(마지막 Conv Layers)
눈, 코, 얼굴 같은 복잡한 패턴을 감지
즉, 필터를 직접 시각화하면 CNN이 어떤 특징을 학습했는지 어느 정도 이해할 수 있음!
- 특징 맵(Feature Map) 시각화
CNN이 특정한 입력 이미지에 대해 각 필터가 활성화된 부분을 확인하는 방법.
특징 맵을 보면 CNN이 입력 이미지에서 어떤 부분을 중요하게 보고 있는지 알 수 있음.
예제
고양이 사진을 입력하면,
첫 번째 층에서 고양이 귀, 털의 결 같은 로컬 패턴이 강조됨.
중간층에서 얼굴 윤곽, 귀 모양 같은 형태가 강조됨.
마지막 층에서 "고양이"라는 전체 개념을 인식하도록 조합됨.
특징 맵을 보면 CNN이 이미지에서 어떤 부분을 중요하게 학습했는지 알 수 있음!
- Grad-CAM (Gradient-weighted Class Activation Mapping)
CNN이 최종적으로 어떤 부분을 보고 예측을 내렸는지 확인하는 방법
이미지의 어떤 영역이 예측에 가장 큰 영향을 미쳤는지 시각적으로 보여줌.
예제
"고양이"를 분류하는 CNN 모델을 Grad-CAM으로 분석하면?
고양이 얼굴 부위가 빨갛게 강조됨 (CNN이 가장 중요한 특징으로 본 영역)
만약 강아지를 예측했다면? → 강아지의 귀나 코 부분이 강조될 수도 있음.
Grad-CAM을 사용하면 CNN이 "왜" 특정 예측을 했는지 해석하는 데 도움을 줌!
하지만 필터의 역할을 100% 해석하는 것은 어려움
CNN이 학습한 필터를 시각적으로 보면 어떤 필터가 어떤 특징을 감지하는지 어느 정도 이해할 수 있음.
하지만 모든 필터의 역할을 사람이 100% 해석하는 것은 어려움.
특히 깊은 층(Deep Layers)에서는 추상적인 개념을 학습하기 때문에 사람이 직관적으로 이해하기 어려운 경우가 많음.
즉, CNN은 필터를 스스로 최적화하며 특징을 학습하지만, 우리가 필터를 직접 분석하는 데는 한계가 있음!
결론
CNN이 충분한 학습을 하면, 필터는 특정한 특징을 감지하도록 최적화됨.
필터 시각화, 특징 맵, Grad-CAM을 사용하면 CNN이 어떤 특징을 학습했는지 어느 정도 해석할 수 있음.
하지만 CNN의 깊은 층에서 학습된 필터는 너무 추상적이어서 사람이 직관적으로 이해하기 어려울 수도 있음.
즉, CNN이 자동으로 학습한 필터를 우리가 직접 분석하는 방법은 있지만, 100% 해석하는 것은 불가능할 수도 있음!
- 필터 개수가 많을수록 얻는 정보가 풍부해짐
필터 하나를 사용하면 한 가지 패턴만 찾을 수 있어.
하지만 필터를 여러 개 사용하면 서로 다른 특징을 감지할 수 있어, 결과적으로 더 정확한 분류가 가능해.
예를 들어, 고양이 이미지를 학습한다고 가정해보자.
필터 1: 고양이 귀를 감지하는 필터
필터 2: 눈을 감지하는 필터
필터 3: 수염을 감지하는 필터
필터 4: 전체적인 털 패턴을 감지하는 필터
... (총 10개의 필터)
➡ 각 필터가 서로 다른 부분을 학습하면서, CNN은 점점 더 정확하게 고양이인지 아닌지를 구분할 수 있어!
-
필터 개수와 Feature Map의 관계
필터 개수 = Feature Map 개수
즉, 10개의 필터를 사용하면, 10개의 서로 다른 Feature Map이 생성됨
이 Feature Map을 조합하면서 CNN은 더 풍부한 정보를 얻고, 더 정확한 예측을 수행할 수 있어. -
필터를 1개만 쓰면 안 되는 이유
한 개의 필터만 사용하면 한 가지 패턴만 학습 가능
→ 예를 들어 "수직선만 감지하는 필터"만 있으면, 다른 패턴(수평선, 곡선 등)을 인식하지 못함.
CNN이 다양한 특징을 학습하려면 여러 개의 필터가 필요
필터 개수가 많아질수록 더 많은 패턴을 학습할 수 있어, 따라서 모델 성능이 향상됨
CNN에서 필터가 어떤 정보를 감지하는지 어떻게 알 수 있을까?
CNN을 학습시킬 때 필터가 어떤 특징을 감지하는지 사람이 직접 정해주는 게 아니라, 학습을 통해 자동으로 결정돼!
즉, CNN이 데이터에서 유용한 패턴을 스스로 찾아내는 것이 핵심이야.
- 필터(커널)는 어떻게 학습될까?
CNN에서 필터의 값(가중치, weight)은 역전파(Backpropagation)와 경사하강법(Gradient Descent)을 통해 자동으로 학습돼.
CNN의 필터 학습 과정:
초기 필터 값(가중치)은 랜덤한 값으로 시작
처음에는 필터가 아무런 의미도 없는 무작위 값들이야.
예를 들어,
3×3 크기의 필터라면 9개의 랜덤한 숫자로 채워져 있음.
필터를 사용하여 입력 이미지에 Convolution 연산을 수행
입력 이미지에 필터를 적용하여 Feature Map을 생성함.
이 Feature Map을 바탕으로 예측 결과를 만듦.
손실 함수(Loss Function)를 계산하여 모델의 예측 오류를 측정
모델이 얼마나 정답에 가까운지를 평가.
CNN 학습 과정 예제: 고양이 vs 강아지 분류
학습 데이터 (Train Data)
우리가 CNN에 고양이 사진을 입력했다고 하자.
이때 정답(Label)은 '고양이'라고 알려줌.
CNN의 예측 과정
CNN이 입력 이미지를 처리하면서 Feature Map을 생성하고,
최종적으로 Fully Connected Layer에서 예측 결과를 출력층(Output Layer)에 전달.
출력층에서 소프트맥스(Softmax) 활성화 함수를 통해 고양이 vs 강아지 확률값을 계산.
예를 들어, 출력층에서 나온 확률값이:
{고양이: 30%}, {강아지: 70%}
CNN의 예측 결과: 강아지 (틀림)
손실 함수(Loss Function) 계산
CNN은 예측값(강아지)과 실제 정답(고양이)의 차이(오차, Loss)를 계산함.
이때 손실 함수가 사용됨.
손실 함수의 역할
CNN이 틀린 예측을 하면, Loss 값이 커짐
CNN이 정답을 맞추면, Loss 값이 작아짐
손실 함수 예제:
크로스 엔트로피(Cross Entropy Loss) → 다중 클래스 분류에서 사용됨.
MSE(Mean Squared Error, 평균제곱오차) → 회귀 문제에서 사용됨.
예를 들어, 크로스 엔트로피 손실 함수를 사용하면:
정답이 '고양이'이면 정답 레이블(Label)은 [1, 0]
CNN의 예측값이 [0.3, 0.7]이면 Loss 값이 커짐.
즉, 손실 함수는 모델이 틀린 정도를 수치화하여 계산하는 역할!
역전파(Backpropagation) 수행
CNN이 틀린 이유를 분석하고, 필터(가중치)를 조정하는 과정!
CNN은 역전파를 통해 오차가 발생한 원인을 거꾸로 추적.
즉, 필터(커널)의 가중치를 얼마나 수정해야 하는지 계산.
고양이를 강아지라고 예측했으므로, 고양이의 특징을 더 강조하도록 필터를 조정해야 함.
역전파를 통해 CNN의 모든 필터 가중치를 업데이트.
경사하강법(Gradient Descent)을 사용하여 가중치를 조금씩 조정.
다음번에는 고양이를 더 정확하게 예측할 가능성이 높아짐!
즉, CNN은 오차를 최소화하기 위해 역전파를 통해 가중치를 계속 조정하면서 학습함.
오차를 줄이도록 필터의 가중치를 조정(역전파 + 경사하강법)
오차가 줄어들도록 필터 값을 업데이트함.
반복 학습을 거치면서 필터가 점점 의미 있는 특징을 감지하도록 최적화됨.
결과적으로, 필터는 학습 데이터에서 가장 유용한 특징을 자동으로 학습하게 돼!
즉, 사람이 어떤 필터를 사용할지 미리 정하지 않아도, CNN이 알아서 좋은 패턴을 찾아내는 거야.
CNN의 필터는 어떻게 학습될까?
컴퓨터는 처음에 어떤 데이터인지 전혀 모르는 상태야.
하지만 역전파(Backpropagation) + 경사하강법(Gradient Descent)을 사용하면, CNN이 스스로 학습하며 필터를 최적화할 수 있어.
- CNN이 필터(가중치)를 학습하는 과정
CNN은 처음에 필터의 값을 랜덤하게 설정해.
즉, 필터(커널)는 초기에는 아무런 의미도 없는 랜덤한 숫자로 이루어져 있어.
하지만 CNN이 여러 이미지를 학습하면서:
필터를 사용하여 특징 맵(Feature Map)을 생성하고
모델이 예측을 수행한 후
정답과 비교하여 오차(손실, Loss)를 계산한 뒤
오차를 줄이도록 필터 값을 조금씩 수정하는 방식으로 학습해.
필터를 하나씩 학습하는 것이 아니라, 모든 필터가 동시에 학습돼!
CNN에서 필터 학습 과정
CNN의 필터는 병렬로 작동하며, 모든 필터가 한 번에 학습됨.
즉, 처음부터 64개 필터가 동시에 Forward Propagation(순전파)과 Backpropagation(역전파)을 수행함.
필터가 64개라면?
처음부터 모든 64개 필터가 동시에 적용되어 Feature Map을 생성
Feature Map이 다음 Layer로 전달되어 연산됨
최종적으로 FC Layer에서 출력값을 얻고, 손실 함수(Loss)를 계산
역전파를 수행하여 64개 필터의 가중치를 동시에 수정
경사하강법을 적용하여 필터 64개를 동시에 업데이트
이 과정이 반복되면서 64개 필터가 점점 더 의미 있는 패턴을 학습함
그럼 필터들은 어떤 순서로 의미 있는 형태가 될까?
처음에는 64개 필터가 모두 랜덤한 값을 가짐 (즉, 아무 의미 없는 상태)
몇 번의 학습을 거치면서 유용한 특징을 학습하는 필터들이 생김
CNN의 깊은 층으로 갈수록 더 추상적인 특징을 감지하는 필터로 발전
특정 필터는 엣지를 감지하고, 특정 필터는 텍스처를 감지하는 등 역할이 나뉘게 됨
즉, 특정 필터가 먼저 의미를 가지는 것이 아니라, 처음부터 모든 필터가 학습되면서 점점 더 의미 있는 패턴을 배우게 된다!
에포크(Epoch)와 CNN 학습 과정
모든 필터가 동시에 끝까지 가고, 역전파를 보내는 과정은 에포크 설정에 따라 반복돼.
즉, 에포크(Epoch)는 CNN이 전체 데이터셋을 몇 번 반복해서 학습할지 결정하는 값이야.
에포크란?
1 에포크(Epoch) = 전체 데이터셋을 한 번 학습하는 과정
에포크가 100이면, 전체 데이터셋을 100번 반복해서 학습하는 것
각 에포크마다 순전파(Forward) → 손실 계산 → 역전파(Backward) → 필터 업데이트가 이루어짐
CNN의 학습 과정과 에포크의 관계
첫 번째 에포크 (Epoch 1)
입력 데이터를 CNN에 전달 → 모든 필터(64개)가 동시에 적용됨
Convolution → Pooling → Flatten → Fully Connected → Output (예측 수행)
정답과 비교하여 손실(Loss) 계산
역전파(Backpropagation) → 경사하강법(Gradient Descent)으로 필터(가중치) 업데이트
아직 학습 초기라 필터가 랜덤한 상태이며, 의미 없는 패턴이 많음
두 번째 에포크 (Epoch 2)
같은 과정을 반복하면서 필터가 조금 더 의미 있는 특징을 학습
Loss가 조금 줄어들고, 모델이 더 나은 예측을 할 수 있도록 개선됨
에포크 반복 (Epoch 3~99)
반복할수록 필터가 더 좋은 패턴을 학습하면서 성능이 향상됨
마지막 에포크 (Epoch 100)
100번째 반복까지 학습이 끝나면, 필터들이 최적화되어 유용한 특징을 감지할 수 있게 됨
Loss가 충분히 감소하고, 모델이 학습을 완료함
에포크와 역전파(Backpropagation)의 관계
각 에포크마다 순전파(Forward)와 역전파(Backward)가 한 번 수행됨
즉, 에포크 1번 = 모든 필터가 순전파 → 예측 수행 → 손실 계산 → 역전파 수행 → 필터 업데이트 1번
에포크가 많아질수록 필터가 점점 최적화됨
너무 적은 에포크는 충분한 학습이 안 되어서 성능이 낮음(Underfitting)
너무 많은 에포크는 과적합(Overfitting) 위험이 있음 → 적절한 에포크 설정이 중요!
이 과정에서 중요한 개념이 바로 역전파(Backpropagation)와 경사하강법(Gradient Descent)이야!
예측은 어디에서 수행될까?
Fully Connected Layer(완전연결층) + Classification 단계에서 예측이 수행됨.
입력 이미지가 여러 개의 Convolution Layer와 Pooling Layer를 지나면서 Feature Map이 생성됨.
마지막에 Flatten Layer를 거쳐 1차원 벡터 형태로 변환됨.
이 벡터는 Fully Connected Layer(Dense Layer)에 입력됨.
마지막 출력층(Output Layer)에서 소프트맥스(Softmax) 또는 시그모이드(Sigmoid) 같은 활성화 함수를 통해 각 클래스에 대한 확률값이 나옴.
예를 들어, 숫자 이미지(09)를 분류하는 모델이라면, 출력층에서 각 숫자에 대한 확률값을 반환함.
가장 확률이 높은 값을 CNN의 예측값(Prediction)으로 사용함.
즉, 예측은 Fully Connected Layer + Classification 단계에서 수행됨!
"각 클래스(Class)"가 뭐야?
클래스(Class)란?
→ CNN이 분류해야 하는 대상(카테고리)
예를 들어:
고양이 vs 개를 분류하는 모델이면, 클래스는 2개 → ["고양이", "개"]
손글씨 숫자(MNIST 데이터셋)를 분류하는 모델이면, 클래스는 10개 → ["0", "1", "2", ..., "9"]
꽃 이미지(3종류)를 분류하는 모델이면, 클래스는 3개 → ["장미", "해바라기", "튤립"]
즉, "각 클래스에 대한 확률값"이란 모델이 각 클래스 중 어느 것인지 예측한 확률을 의미함!
CNN이 숫자(0~9)를 분류하는 경우
출력층에서 CNN이 각 숫자(0~9)에 대해 확률을 반환한다고 했지?
이게 무슨 의미인지 예제를 보자!
입력 이미지:
CNN에 "숫자 7" 이미지를 입력했다고 가정
출력층에서 계산된 확률값:
CNN은 숫자 0~9 중에서 어떤 숫자인지 예측해야 함.
출력층에서 소프트맥스(Softmax) 활성화 함수를 사용하면, 각 클래스(0~9)에 대한 확률값이 나오게 됨.
예를 들어, 출력층에서 나온 확률값이 이렇다고 해보자:
[0.01,0.05,0.03,0.02,0.08,0.02,0.05,0.70,0.02,0.02]
이걸 보면:
0일 확률: 1%
1일 확률: 5%
2일 확률: 3%
…
7일 확률: 70% (가장 높은 확률)
…
9일 확률: 2%
CNN은 출력층에서 확률이 가장 높은 값을 정답으로 예측함.
➡ 이 경우 CNN의 최종 예측 결과는 "숫자 7"이 됨!
즉, CNN은 출력층에서 각 클래스에 대한 확률을 계산하고, 그중 가장 높은 확률을 가진 클래스를 최종 예측으로 선택함!
소프트맥스(Softmax) 활성화 함수가 하는 일
출력층에서 확률값을 얻는 핵심이 바로 소프트맥스(Softmax) 활성화 함수야.
Softmax는 모든 숫자를 확률값(0~1)로 변환하고, 총합이 1이 되도록 함.
즉, CNN이 특정 숫자일 가능성을 확률로 나타내고, 확률이 가장 높은 클래스를 예측값으로 선택하는 거야!
정리
"각 클래스"란, CNN이 분류해야 하는 대상 (예: 숫자 0~9, 고양이/개, 꽃 종류 등)
출력층에서 나온 확률값은 CNN이 각 클래스에 대해 얼마나 가능성이 높은지 나타낸 값
CNN은 확률값이 가장 높은 클래스를 최종 예측값으로 선택
소프트맥스(Softmax) 활성화 함수가 확률을 계산하여 총합이 1이 되도록 변환함
CNN은 정답을 어떻게 비교할까?
손실 함수(Loss Function)를 사용하여 CNN의 예측값과 정답(Label)을 비교함.
정답(Label)은 데이터셋에서 제공됨.
예를 들어, 고양이 이미지가 주어졌다면 정답(Label)은 '고양이'로 지정됨.
모델이 고양이 이미지를 보고 "이건 개일 것 같다 (개일 확률이 더 높음)"라고 예측하면, CNN이 틀린 거야.
이때, CNN의 예측값(출력층의 값)과 정답(Label)의 차이를 계산하는 것이 오차(손실, Loss)야.
즉, 정답(Label)은 데이터셋에서 주어지며, Fully Connected Layer에서 나온 CNN의 예측값과 비교하여 오차를 계산함.
오차(Loss)는 어디서 계산될까?
손실 함수(Loss Function)를 통해 오차를 계산하고, 역전파(Backpropagation) 과정에서 이를 줄이도록 필터를 수정함.
오차는 출력층(Output Layer)에서 계산됨.
대표적인 손실 함수:
크로스 엔트로피(Cross-Entropy Loss) → 다중 분류 문제에서 사용됨.
MSE(Mean Squared Error, 평균제곱오차) → 회귀 문제에서 사용됨.
예를 들어, CNN이 "고양이"라고 예측해야 하는데, "개"라고 예측했다면:
정답(Label) = 1, 0, 0
모델 예측값 = [0.2, 0.7, 0.1] (개일 확률이 가장 높음)
이를 비교하여 손실 값(Loss)을 계산함.
즉, 오차(손실, Loss)는 Fully Connected Layer의 출력값과 정답(Label) 간의 차이를 계산하여 측정됨.
CNN은 오차를 줄이기 위해 어떻게 학습할까?
역전파(Backpropagation) + 경사하강법(Gradient Descent)으로 필터(가중치)를 수정함.
역전파(Backpropagation) 수행
출력층에서 계산된 오차(Loss)를 거꾸로 전파(Backpropagation)하여 CNN의 가중치(필터 값)를 얼마나 수정해야 할지 계산.
즉, "CNN의 필터(가중치)가 잘못된 예측에 얼마나 기여했는지"를 평가하여 수정할 값을 결정.
경사하강법(Gradient Descent) 적용
필터의 가중치를 오차를 줄이는 방향으로 업데이트함.
손실 함수의 기울기(Gradient)를 계산하여, 가중치를 조금씩 변경하면서 손실 값을 줄여나감.
여러 번 반복하면서 최적의 필터 값을 찾아감.
즉, 오차(손실)를 계산한 후, 역전파와 경사하강법을 사용하여 CNN의 필터 값을 계속 수정하면서 학습함.
CNN 학습 과정: 전체 정리
입력 이미지 → Convolution + Pooling을 거쳐 특징을 추출
Flatten → Fully Connected Layer를 통해 최종 예측값을 생성
출력층에서 예측값과 정답(Label)을 비교하여 오차(Loss) 계산
오차를 줄이기 위해 역전파(Backpropagation) 수행
경사하강법(Gradient Descent)으로 필터(가중치)를 업데이트하여 학습 진행
반복 학습을 통해 CNN의 필터가 점점 최적화됨
- 역전파(Backpropagation)란?
"필터 값을 어떻게 조정해야 오차를 줄일 수 있을까?"
CNN은 이미지를 보고 예측을 한 후, 정답과 비교해서 예측이 얼마나 틀렸는지(오차)를 계산해.
이때, 틀린 정도를 바탕으로 필터의 값을 조정하는 알고리즘이 역전파야.
역전파의 핵심 아이디어:
예측 결과가 정답과 얼마나 차이가 있는지 계산 (손실 함수, Loss Function)
오차가 발생한 원인을 거꾸로 추적하여 가중치를 수정
즉, 필터 값(가중치)이 얼마나 영향을 미쳤는지 계산하고, 그에 따라 조정
역전파 과정
CNN이 이미지를 입력받아 예측값(출력값)을 생성
예측값과 실제 정답(레이블) 사이의 차이(손실)를 계산
예: 손실 함수(loss function) = MSE(평균제곱오차), 크로스 엔트로피 등
오차를 네트워크의 뒤쪽(출력층)에서 앞쪽(입력층)으로 거꾸로 전달
각 필터(가중치)가 결과에 미친 영향을 계산(편미분, Gradient 계산)
경사하강법을 사용하여 가중치를 조정
- 경사하강법(Gradient Descent)이란?
"오차를 줄이기 위해 필터 값을 어떻게 바꿔야 할까?"
경사하강법은 필터 값을 조금씩 수정하면서 오차를 최소화하는 방법이야.
즉, 손실 함수(Loss Function)가 가장 작은 지점을 찾도록 필터 값을 조정하는 알고리즘이야.
경사하강법의 핵심 아이디어:
손실 함수의 기울기(Gradient)를 계산
손실 함수가 필터(가중치)에 따라 어떻게 변하는지 미분하여 계산
즉, "이 필터를 어떻게 조정하면 오차가 줄어드는지" 방향을 알아냄
기울기가 낮아지는 방향으로 가중치를 업데이트
α (학습률, Learning Rate)는 가중치를 얼마나 크게 조정할지 결정하는 하이퍼파라미터
반복하면서 오차를 점점 줄여 최적의 필터 값을 찾음
경사하강법은 미끄러운 산을 내려가는 것과 비슷해.
산 꼭대기(오차가 큰 상태)에서 시작해서, 오차가 가장 작은 곳(최적의 가중치)을 찾아 내려가는 것이 목표야.
- CNN의 학습 과정 정리
이제 CNN이 필터를 학습하는 전체 과정을 정리해볼게!
초기 상태
CNN은 무작위 필터(랜덤한 가중치)를 사용하여 예측을 수행
초기에는 필터가 의미 있는 패턴을 찾지 못함 (무작위 추측)
순전파(Forward Propagation)
입력 이미지를 필터와 합성곱(Convolution)하여 Feature Map 생성
Feature Map을 Activation Function (예: ReLU)으로 비선형 변환
마지막 Fully Connected Layer에서 최종 예측 수행
손실 계산 (Loss Calculation)
예측값과 실제 정답을 비교하여 손실(오차)을 계산
예: 크로스 엔트로피, MSE 등
역전파 (Backpropagation)
손실을 줄이기 위해 필터가 얼마나 영향을 미쳤는지 계산(Gradient 계산, 편미분)
네트워크의 뒤쪽에서 앞쪽으로 오차 정보를 거꾸로 전달
경사하강법 (Gradient Descent)
손실이 줄어드는 방향으로 필터 값을 조금씩 조정
반복 학습하면서 점점 더 좋은 필터로 최적화됨
최적화 완료!
CNN이 여러 번 학습한 후, 필터는 데이터에서 중요한 패턴을 감지하는 형태로 최적화됨!
이제 CNN은 특정 특징(예: 엣지, 눈, 얼굴)을 감지하는 필터를 자동으로 학습함!
-
결론
CNN은 처음에는 랜덤한 필터를 사용하지만, 학습을 거치면서 최적의 필터 값을 찾아감
역전파(Backpropagation)를 사용하여 필터가 오차에 얼마나 영향을 미쳤는지 계산하고
경사하강법(Gradient Descent)을 사용하여 필터 값을 업데이트하면서 점점 최적화됨
결과적으로 CNN은 데이터에서 중요한 특징을 자동으로 학습할 수 있음! -
CNN의 필터가 학습하는 패턴의 종류
CNN의 층이 깊어질수록 필터가 감지하는 정보도 점점 더 추상적인 특징을 학습하게 돼.
CNN의 초기층(Shallow Layers)
저수준 특징(Low-Level Features)을 학습
엣지(Edge), 선(Line), 색상(Color), 텍스처(Texture) 같은 기본적인 패턴을 감지
예를 들어, 흰색과 검은색의 경계를 찾는 필터가 있을 수 있음.
CNN의 중간층(Mid-Level Layers)
좀 더 복잡한 패턴을 감지
예를 들어, 곡선(Curve), 모서리(Corner), 특정한 패턴들을 인식
고양이 얼굴의 윤곽이나 눈, 코 같은 형태를 감지할 수도 있음.
CNN의 깊은 층(Deep Layers)
고수준 특징(High-Level Features)을 학습
예를 들어, 얼굴 전체, 자동차의 실루엣, 숫자 모양 같은 구체적인 개체를 인식할 수 있음.
이 단계에서 CNN은 "이건 고양이" 또는 "이건 자동차" 같은 분류를 수행할 수 있음.
즉, CNN의 필터는 층이 깊어질수록 더 추상적이고 고차원적인 정보를 학습하게 돼!
- 학습된 필터를 직접 보는 방법
CNN이 학습한 필터가 어떤 특징을 감지하는지 시각적으로 확인할 수도 있어.
일반적으로 다음과 같은 방법을 사용해!
1) 필터 시각화(Filter Visualization)
학습된 CNN의 초기층 필터(Conv Layer 1~2)를 시각화하면, 필터가 감지하는 패턴을 직접 볼 수 있어.
보통 첫 번째 층의 필터들은 엣지(Edge), 선(Line) 같은 저수준 특징을 감지하는 걸 볼 수 있음.
예시: 필터가 밝은 부분과 어두운 부분을 감지하는 경우, 엣지를 찾는 역할을 하는 걸 알 수 있음.
2) Feature Map 시각화(Activation Map)
특정 이미지가 주어졌을 때 CNN이 각 계층에서 어떤 특징을 활성화하는지 확인 가능.
중간 Feature Map을 출력하면, 어떤 부분이 강조되는지 확인할 수 있음.
3) Grad-CAM(Gradient-weighted Class Activation Mapping)
CNN이 어떤 부분을 보고 최종 결정을 내렸는지 시각화하는 기법.
예를 들어, "고양이"라고 예측했다면, CNN이 이미지에서 어떤 영역을 중요하게 봤는지 확인할 수 있음.
이런 방법들을 사용하면 CNN이 실제로 어떤 패턴을 학습했는지 확인할 수 있어!
- 결론: 필터는 학습을 통해 자동으로 최적화됨!
CNN의 필터는 처음에는 랜덤한 값이지만, 훈련 데이터로 학습하면서 점점 의미 있는 특징을 감지하도록 변함.
층이 깊어질수록 필터가 감지하는 정보도 단순한 선 → 곡선 → 얼굴 같은 복잡한 패턴으로 발전.
CNN이 어떤 필터를 학습했는지 직접 시각화할 수도 있음.
사람이 직접 필터를 설계하는 것이 아니라, CNN이 데이터에서 가장 중요한 특징을 스스로 학습하는 것이 핵심!
필터는 CNN이 데이터에서 자동으로 학습하는 것이고, 각 층마다 다른 수준의 특징을 감지하도록 최적화됨!
왜 활성함수(Activation function)을 쓰고 이건 무엇일까?
간단히 말하자면 선형함수(linear function)인 convolution에 비선형성(nonlinearity)를 추가하기 위해 사용하는 것입니다.
CNN에서 왜 활성화 함수(Activation Function)를 사용하는가?
CNN에서 Convolution Layer(합성곱 층)는 Convolution(합성곱) + Activation Function(활성화 함수)로 구성됨.
즉, Convolution 연산 후에 활성화 함수를 적용하는 이유는 무엇일까?
활성화 함수는 비선형성(Non-linearity)을 추가하기 위해 사용됨.
CNN에서 비선형성을 추가하지 않으면 뉴럴 네트워크가 단순한 선형 모델이 되어버려 복잡한 패턴을 학습할 수 없음!
Convolution 연산(합성곱)은 선형 연산(Linear Operation)
CNN에서 Convolution 연산은 기본적으로 선형 함수(Linear Function)처럼 동작해.
선형 함수란?
입력
x 에 대해 출력이 선형적인 변화만 하는 함수
y=ax+b
직선 형태의 관계만 학습 가능하고, 복잡한 패턴을 학습할 수 없음.
CNN의 Convolution 연산도 기본적으로 선형 연산임!
필터(커널)를 이용해 입력 데이터를 변형하는 연산이지만, 여전히 선형적인 변환만 가능.
따라서 비선형성을 추가하지 않으면, CNN이 단순한 선형 모델이 되어 복잡한 패턴을 학습할 수 없음.
CNN에서 비선형성이 필요한 이유
CNN이 학습하려는 데이터(예: 이미지)는 단순한 직선 관계가 아님.
이미지 속 패턴은 곡선, 다양한 형태, 복잡한 구조를 가지므로, 모델이 이를 학습하려면 비선형성이 필요함!
활성화 함수(Activation Function)는 CNN에 비선형성을 추가하여 복잡한 패턴을 학습할 수 있도록 해줌!
ex)
cdr3 영역 10자리 아미노산 서열의 각 임베딩 벡터 1280 개
총 10 X 1280 짜리 데이터인데,
어느 위치의, 어느 임베딩 벡터가 중요한 데이터인지는 직선으로 따져질 확률이 매우 낮음
복잡한 데이터이기 때문에, 중요한 데이터를 구분하기 위해서는 직선이 아닌 곡선으로 경계를 설정해야 할 가능성이 높음
그렇기 때문에 비선형성을 추가하는 것
주요 활성화 함수(Activation Function)
CNN에서는 ReLU(Rectified Linear Unit)이 가장 많이 사용됨.
다른 활성화 함수도 있지만, CNN에서 주로 사용되는 함수들을 정리해볼게!
- ReLU (Rectified Linear Unit)
f(x)=max(0,x)
양수는 그대로 출력, 음수는 0으로 변환
비선형성을 추가하면서도 계산이 간단하여 CNN에서 가장 많이 사용됨
Gradient Vanishing 문제를 방지하여 깊은 네트워크에서도 잘 작동함
음수 값을 0으로 만들어 sparsity(희소성) 효과를 제공 → 학습 효율 증가
희소성(Sparsity)이란?
희소한(Sparse) 데이터란 대부분의 값이 0이고, 일부 값만 중요한 데이터를 의미함.
CNN에서 ReLU를 사용하면 많은 뉴런 값이 0이 되어 희소한 표현(Sparse Representation)이 생성됨.
즉, ReLU는 CNN이 불필요한 정보를 제거하고, 중요한 특징만 학습할 수 있도록 도와줌!
ReLU의 희소성 효과가 학습을 빠르게 하는 이유
CNN에서 ReLU의 희소성(Sparsity) 효과는 다음과 같은 학습 효율 증가 효과를 가짐!
- 연산량 감소 → 학습 속도 증가
ReLU는 음수 값을 0으로 만들어 많은 뉴런이 비활성화(즉, 계산되지 않음)됨.
즉, 불필요한 뉴런을 제거하여 연산량이 감소하고 학습 속도가 빨라짐!
특히 CNN처럼 수천만 개의 뉴런을 가진 대형 네트워크에서 매우 효과적!
ReLU를 사용하면 계산량이 줄어들어 CNN이 더 빠르게 학습 가능!
-
과적합(Overfitting) 방지 효과
뉴런의 일부를 강제로 0으로 만들어서 과적합을 방지하는 효과가 있음.
네트워크가 모든 뉴런을 활성화하면 불필요한 특징까지 학습하여 과적합될 위험이 있음.
하지만 ReLU는 일부 뉴런만 활성화하여, 모델이 더 일반화된 특징을 학습하도록 유도!
ReLU를 사용하면 CNN이 더 강건한(Generalizable) 모델이 됨! -
중요한 특징을 더 강조하는 효과
음수 값을 제거하면 양수 값이 더 강하게 표현됨.
즉, CNN이 정말 중요한 특징에 더 집중하여 학습할 수 있음!
예제: 이미지 필터링
CNN이 엣지(Edge)나 텍스처(Texture) 같은 특징을 학습할 때,
ReLU가 약한 특징(음수 값)을 제거하고, 강한 특징(양수 값)을 강조하는 역할을 함!
ReLU를 사용하면 CNN이 중요한 특징을 더 효과적으로 학습 가능!
CNN에서 ReLU를 많이 쓰는 이유:
연산이 빠름 (지수 연산이 없음)
기울기(Gradient)가 사라지는 문제(Vanishing Gradient)를 완화
CNN의 특성상 음수 값은 정보 손실을 줄 가능성이 낮음
(ReLU가 음수 값을 0으로 변환해도 CNN에서는 정보 손실이 크지 않다)
CNN에서는 거의 모든 Convolution Layer 뒤에 ReLU가 사용됨!
CNN에서 음수 값이 의미하는 것
CNN에서 Convolution 연산(합성곱 연산)을 하면 필터(커널)가 이미지에서 특징을 감지해.
이때, 합성곱 결과(Feature Map)의 값들은 양수와 음수로 나뉘게 돼.
양수 값(+) → 입력 이미지에서 특정 특징이 강하게 존재하는 부분
음수 값(-) → 입력 이미지에서 특정 특징이 거의 없거나, 약한 부분
즉, 음수 값은 필터가 감지하려는 특징이 약한 곳을 의미하는 경우가 많아!
ReLU가 음수 값을 0으로 만들면 CNN에 문제가 될까?
ReLU는 음수 값을 0으로 변환하는데, 이 과정에서 정보 손실이 크지 않은 이유가 있어!
음수 값은 필터가 감지하는 특징이 약한 부분이므로, 0으로 변환해도 중요한 정보가 사라지는 게 아님!
- Sigmoid (시그모이드)
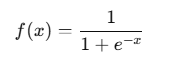
출력이 0~1 범위로 조정됨 → 확률 값으로 사용 가능
초기 CNN에서 사용되었지만, 깊은 네트워크에서는 잘 사용되지 않음
이유: Gradient Vanishing(기울기 소실) 문제가 발생하여 학습이 어려움
지금은 출력층에서 이진 분류(Binary Classification)에서만 사용
- Softmax
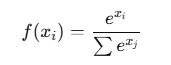
다중 클래스 분류(Multi-class Classification)에서 출력층에 사용
모든 출력 값이 0~1 범위로 정규화되고, 총합이 1이 됨
CNN에서 이미지 분류(예: 0~9 숫자 분류)할 때 최종적으로 사용됨
즉, Softmax는 마지막 출력층에서 클래스 확률을 계산하는 역할!
CNN에서 활성화 함수가 적용되는 위치
CNN에서는 활성화 함수가 각 합성곱(Convolution) 연산 후에 적용됨.
예제: CNN의 기본 구조
입력 데이터 (이미지 or 벡터) → Convolution 연산 → ReLU(활성화 함수) → Pooling → 다음 계층으로 전달
여러 개의 Convolution + ReLU 계층을 거친 후, Fully Connected Layer(FC Layer) → Softmax로 확률 예측
즉, 활성화 함수는 CNN이 비선형성을 학습할 수 있도록 도와주는 핵심 요소!
활성화 함수가 없으면 CNN이 어떻게 될까?
만약 CNN에서 활성화 함수를 사용하지 않는다면?
CNN은 단순한 선형 모델(Linear Model)이 되어버려서 복잡한 패턴을 학습하지 못함!
활성화 함수가 없으면, CNN의 모든 레이어가 단순한 행렬 곱셈과 덧셈만 수행
네트워크가 아무리 깊어져도, 모델이 단순한 선형 변환만 수행하는 것과 동일해짐
결국 CNN은 데이터의 복잡한 특징을 학습할 수 없게 됨
활성화 함수는 CNN이 "단순한 선형 변환을 넘어서 복잡한 패턴을 학습할 수 있도록 만드는 필수 요소!"
결론
CNN에서 활성화 함수(Activation Function)는 비선형성을 추가하는 역할
Convolution 연산은 기본적으로 선형(Linear) 변환이므로, 비선형성이 없으면 패턴을 학습할 수 없음
ReLU는 CNN에서 가장 널리 사용되며, 빠르고 Gradient Vanishing 문제를 완화
Softmax는 마지막 출력층에서 클래스 확률을 계산할 때 사용됨
활성화 함수가 없으면 CNN이 단순한 선형 모델이 되어 학습이 불가능함
비선형성(Non-linearity)이란?
선형 함수의 문제점
선형 함수만으로는 복잡한 관계를 학습할 수 없음!
예를 들어, 고양이와 개를 구분하는 문제에서, 모든 데이터가 직선 하나로 나뉠 수 없다면?
이런 복잡한 패턴을 학습하려면 비선형 함수(Non-linear Function)가 필요함!
비선형 함수(Non-linear Function)란?
출력이 입력값에 대해 선형적이지 않게 변하는 함수
그래프를 그리면 곡선(Curve)이 포함됨!
즉, 데이터가 단순한 직선으로 구분되지 않을 때, 곡선을 활용하여 구분할 수 있도록 해줌
예제:
이차 함수 (곡선 모양)
f(x)=sin(x) (주기적인 패턴)
ReLU, Sigmoid, Softmax 등 활성화 함수는 전부 비선형 함수!
비선형 함수의 장점
복잡한 패턴을 학습할 수 있음!
곡선 형태로 데이터를 나눌 수 있어, CNN이 더 강력한 표현력을 가짐.
예제: 활성화 함수 없이 vs 활성화 함수 적용
CNN에서 활성화 함수가 없을 때와 있을 때의 차이를 비교해보자!
Case 1: 활성화 함수 없이 CNN을 학습한다면?
CNN이 Convolution 연산만 수행 (즉, 단순한 선형 변환만 적용)
네트워크가 깊어져도 결국 하나의 선형 변환(행렬 곱셈)으로 합쳐져 버림
즉, CNN이 복잡한 패턴을 학습할 수 없음!
단순한 직선 경계(Linear Boundary)만 학습 가능!
결과:
CNN이 복잡한 이미지 패턴을 학습할 수 없어서 성능이 나빠짐!
Case 2: 활성화 함수(ReLU)를 적용한 CNN
Convolution 연산 후 ReLU 활성화 함수 적용
네트워크에 비선형성을 추가하여 곡선 형태로 데이터를 나눌 수 있음!
CNN이 더 깊어질수록 더 복잡한 패턴을 학습 가능!
결과:
CNN이 곡선을 포함한 복잡한 데이터 패턴을 학습할 수 있음!
고양이와 개 같은 복잡한 특징을 학습할 수 있어 정확도가 높아짐!
선형 모델은 문제의 답을 직선 하나로 구분하려고 함.
하지만 현실 세계의 데이터는 직선 하나로 나눠지지 않음.
비선형 모델은 곡선을 사용하여 더 정밀하게 분류할 수 있음!
비선형성의 핵심 개념 정리
현실 세계의 데이터는 단순한 직선(선형)으로 구분되지 않는 경우가 많아서, CNN에 비선형성을 추가하여 더 정교한 패턴을 학습하는 것이 핵심이야.
선형 모델 → 단순한 직선(Linear Boundary)로 데이터를 구분
비선형 모델 (활성화 함수 적용) → 곡선(Non-linear Boundary) 형태로 데이터를 구분
즉, ReLU나 Softmax 같은 활성화 함수는 데이터를 비선형적으로 변환하여, CNN이 더 정교한 경계를 학습할 수 있도록 함.
CNN이 더 정교한 경계를 학습할 수 있다는 의미
CNN에서 ReLU 같은 활성화 함수(비선형성)를 추가하면, 신경망이 데이터의 "경계(Boundary)"를 더 정교하게 학습할 수 있다고 했지?
그럼, 여기서 "경계를 학습한다"는 게 무슨 의미인지 자세히 설명해볼게!
데이터 분류에서 "경계(Boundary)"란?
CNN이 이미지를 분류할 때, 각 클래스(예: 고양이 vs 개)를 구분하는 기준(Decision Boundary)을 학습해야 함!
데이터가 단순하면?
고양이와 개가 직선(Linear Boundary) 하나로 깔끔하게 나뉠 수도 있음.
데이터가 복잡하면?
직선 하나로 구분할 수 없고, 곡선(Non-linear Boundary)이 필요할 수도 있음.
ex) 단백질 임베딩 벡터에서, 해당 임베딩벡터의 어느 부분을 통해 결합친화도를 판별할지는 곡선으로 구분해야할 가능성이 높음(직선 형태로 깔끔히 데이터가 구분되지는 않을 확률이 높기 때문에)
CNN이 하는 일?
학습을 통해 데이터의 패턴을 찾고, 어떤 기준(경계)으로 데이터를 나눌지 결정함.
선형 모델(Linear Model)과 비선형 모델(Non-linear Model)의 차이
만약 CNN이 비선형성을 추가하지 않는다면?
CNN이 단순한 선형 함수(Linear Function)만 사용한다면, 데이터를 나누는 경계도 직선(Linear)만 가능
즉, 모든 고양이 데이터가 한쪽, 모든 개 데이터가 다른 쪽에 있도록 직선으로 나누려고 함
예제: 직선 경계(Linear Boundary)
왼쪽이 고양이 🐱, 오른쪽이 개 🐶라면?
직선 하나로 데이터를 나누는 방법밖에 없음!
🐱 🐱 🐱 | 🐶 🐶 🐶
하지만 실제 데이터는 이렇게 깔끔하게 나뉘지 않음
CNN이 비선형성을 추가하면?
비선형 활성화 함수(ReLU, Softmax 등)를 사용하면, 직선이 아니라 곡선 형태의 경계(Non-linear Boundary)도 학습 가능!
예제: 곡선 경계(Non-linear Boundary)
실제로 데이터가 이렇게 섞여 있다면?
🐱 🐱 🐶 | 🐶 🐱 🐶
🐱 🐱 🐶 | 🐶 🐱 🐶
🐱 🐱 🐶 | 🐶 🐱 🐶
단순한 직선 하나로는 분류할 수 없음!
CNN이 비선형성을 활용하면 데이터 모양에 맞게 곡선으로 경계를 설정할 수 있음!
즉, CNN이 비선형성을 추가하면 "단순한 직선이 아니라 더 복잡한 곡선 형태로 데이터를 구분할 수 있는 것!"
-
선형 모델 (직선 경계)
선형 모델(Linear Model)만 사용하면, 데이터가 단순한 직선으로만 나뉨
하지만 실제 데이터는 복잡한 곡선 형태로 분포될 수도 있음!
이런 경우 고양이와 개를 완벽하게 분류하지 못함.
문제: 직선으로 나눌 수 없는 데이터! -
비선형 모델 (곡선 경계)
CNN이 활성화 함수(ReLU 등)를 사용하여 비선형성을 추가하면?
단순한 직선이 아니라, 곡선으로 데이터 분포에 맞춰 경계를 설정할 수 있음!
더 복잡한 패턴도 학습 가능!
곡선으로 데이터 분포에 맞춰 분류 가능
CNN에서 "정교한 경계를 학습한다"는 의미
CNN이 단순한 직선이 아니라, 데이터 모양에 맞는 곡선 형태의 경계를 학습할 수 있다는 뜻!
ReLU 같은 활성화 함수가 비선형성을 추가하여, CNN이 복잡한 패턴을 학습할 수 있도록 도와줌!
결과적으로 더 정확한 예측이 가능해짐!
ReLU(렐루)를 적용하면 데이터가 어떻게 변할까?
f(x)=max(0,x)
입력값
x 가 0 이상이면 그대로 출력, 0 미만이면 0으로 변환
음수 값을 모두 제거하고, 양수만 유지하는 특성이 있음
ReLU를 적용하면 데이터의 변화
원래 데이터가 대칭적(-, + 값 포함)으로 분포되어 있을 수 있음.
ReLU를 적용하면 음수 데이터가 모두 0으로 변하고, 양수 데이터는 그대로 유지됨.
즉, 데이터의 분포가 한쪽(양수 방향)으로만 편향됨.
결과:
네트워크가 비선형성을 가지면서도, 선형처럼 연산이 단순해짐
ReLU는 입력 값을 0 이상으로 유지하면서 음수 데이터를 없애는 효과
CNN이 필요 없는 음수 값을 제거하고, 중요한 특징을 강조하는 효과
ReLU 적용 전 vs 적용 후
입력 데이터 (x) ReLU 적용 결과 (f(x) = max(0, x))
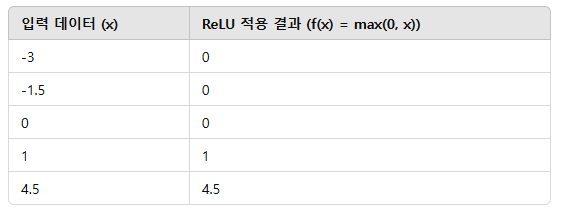
즉, ReLU는 음수를 0으로 변환하여, CNN이 중요한 특징을 더 효과적으로 학습하도록 함.
Softmax를 적용하면 데이터가 어떻게 변할까?
Softmax는 입력값을 확률 형태(0~1)로 변환하고, 총합이 1이 되도록 정규화함.
즉, CNN이 여러 개의 클래스를 예측할 때, 각 클래스에 대한 확률을 계산하는 역할!
Softmax를 적용하면 데이터의 변화
입력값이 크면 더 큰 확률을 가지도록 변환
작은 값은 더 작아지고, 큰 값은 더 커지는 형태로 확률 분포를 강조
모든 출력의 총합이 1이 되도록 정규화됨 → 확률로 해석 가능
결과:
Softmax를 적용하면 모든 출력이 확률 값(0~1)로 변환됨
CNN이 각 클래스(예: 고양이, 개, 사람 등)에 대한 예측 확률을 계산할 수 있도록 변환함
값이 상대적으로 클수록 확률이 높아지며, 다른 값들과의 차이를 더욱 강조함
Softmax 적용 전 vs 적용 후
원래 값 (Logits) Softmax 적용 후 (확률)
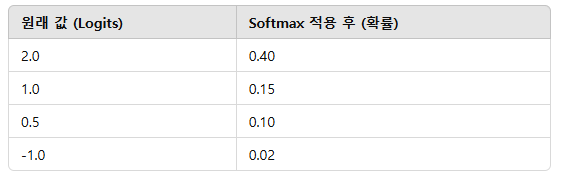
즉, Softmax는 입력값을 확률로 변환하여, CNN이 특정 클래스에 대한 신뢰도를 계산할 수 있도록 함.
첫번째 Pooling Layer
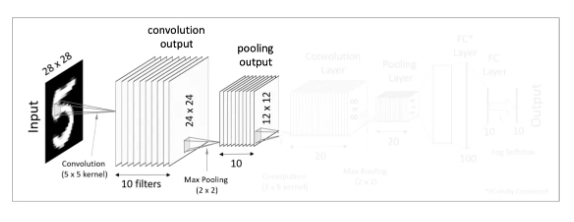
우선 Pooling이라는 개념이 무엇인지 짚고 넘어가야 합니다.
이 전 단계에서 convolution 과정을 통해 많은 수의 결과값(이미지)들을 생성했습니다. 하지만 위와 같이 한 개의 이미지에서 10개의 이미지 결과값이 도출되어버리면 값이 너무 많아졌다는 것이 문제가 됩니다. 때문에 고안된 방법이 Pooling이라는 과정입니다. Pooling은 각 결과값(feature map)의 dimentionality를 축소해 주는 것을 목적으로 둡니다. 즉 correlation이 낮은 부분을 삭제하여 각 결과값을 크기(dimension)을 줄이는 과정입니다.
Pooling이란? 왜 필요한가?
CNN에서 Pooling(풀링)은 Feature Map(특징 맵)의 크기를 줄이는 과정이야.
즉, 너무 많은 데이터(Feature Map)를 효과적으로 정리하여 중요한 정보만 남기는 과정!
CNN이 Convolution 연산을 수행하면, 한 개의 이미지에서 여러 개의 Feature Map이 생성됨
하지만 Feature Map이 너무 많아지면 계산량이 커지고, 불필요한 정보까지 학습될 위험이 있음
Pooling을 사용하면 차원을 줄여서 연산을 최적화하고, 중요한 정보만 남길 수 있음!
즉, Pooling은 "중요한 정보만 유지하면서 Feature Map의 크기를 줄이는 과정"이야!
Pooling의 핵심 개념
Pooling은 CNN이 더 효율적으로 학습할 수 있도록 도와주는 과정!
Feature Map의 크기를 줄여서(차원 축소, Dimensionality Reduction) 계산량을 감소시킴
중요한 특징은 유지하면서, 불필요한 부분(노이즈)은 제거
공간 정보(Spatial Information)를 유지하면서 특징을 요약
즉, Pooling을 하면 "필요한 정보만 유지하면서 데이터 크기를 줄여 학습을 더 효율적으로 할 수 있음!"
Pooling을 왜 해야 할까?
CNN이 Convolution 연산을 하면 Feature Map이 너무 많아지는 문제
예를 들어, 입력 이미지가
32×32 크기라고 하자.
Convolution을 거치면서 Feature Map이 여러 개(예: 10개, 64개) 생성됨.
그런데 CNN이 깊어질수록 Feature Map이 계속 많아지고, 계산량이 증가함.
해결책?
Pooling을 사용해서 Feature Map의 크기를 줄이면, 계산량을 줄이면서도 중요한 정보를 유지할 수 있음!
Pooling을 하면 데이터가 어떻게 변할까?
Feature Map 크기가 작아지면서 학습이 더 효율적으로 진행됨.
이미지의 특징이 유지되면서도, 불필요한 데이터가 제거됨.
위치에 대한 작은 변화(예: 사진이 약간 이동해도 특징이 유지됨 → 위치 변화에 강한 모델을 만듦).
즉, Pooling은 Feature Map을 요약하여 CNN이 더 빠르고 정확하게 학습할 수 있도록 도와줌!
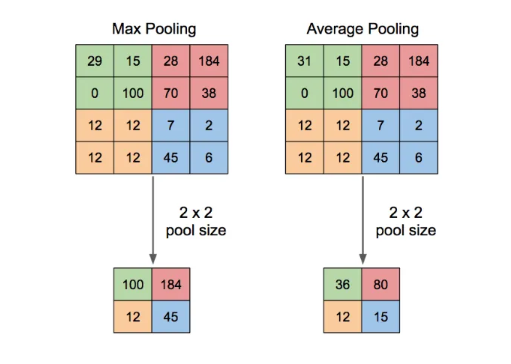
Pooling에는 대표적으로 두가지 방법으로 Max pooling과 Average pooling이 있습니다. 위 이미지와 같이 Pool의 크기가 2x2인 경우 2x2크기의 matrix에서 가장 큰 값(max)이나 평균값(average)를 가져와 결과값의 크기를 반으로 줄여주게 됩니다.
자, 이제 다시 본론으로 돌아가 그 위의 전체 네트워크 이미지로 돌아가면 Pooling Layer의 결과값이 열개의 12x12 matrics가 된 것을 확인할 수 있습니다.
두번째 Convolutional Layer
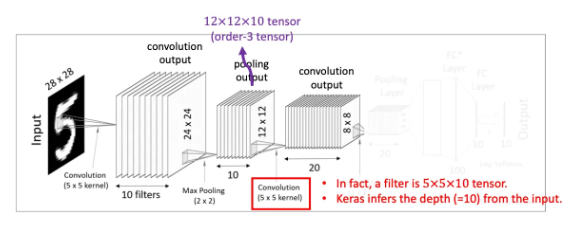
이번 Convolutional layer에서는 텐서 convolution을 적용합니다. 이전의 pooling layer에서 얻어낸 12x12x10 텐서(order-3 tensor)를 대상으로 5x5x10크기의 텐서필터 20개를 사용해 줍니다. 그렇게 되면 각각 8x8크기를 가진 결과값 20개를 얻어낼 수 있습니다.
CNN에서 Feature Map도 3차원 구조로 변함
CNN에서 Convolution과 Pooling을 수행하면, Feature Map(특징 맵)이 생성되는데,
이 Feature Map도 3차원 텐서로 유지됨!
예제: 이전 Layer에서 Pooling 결과가 12×12×10이라면?
너비(Width) = 12
높이(Height) = 12
채널(Channel) = 10 (필터 개수)
→ 즉, 이 Feature Map도 3D 텐서(12 × 12 × 10)!
CNN의 모든 연산은 3D 텐서를 유지하면서 수행됨!
필터(커널)도 3D 형태로 적용해야 함
CNN에서 Convolution을 할 때, 필터도 이미지(Feature Map)와 같은 차원을 가져야 함!
필터도 3D 텐서로 만들어야, 입력과 올바르게 곱할 수 있음!
예제: 3D 필터 적용
Feature Map 크기:
12×12×10
필터 크기:
5×5×10 (너비 × 높이 × 채널)
필터 개수: 20개
즉, 필터도 Feature Map과 같은 채널 수(10)를 가져야 연산이 가능함!
필터가 3D 텐서이기 때문에, 모든 채널에서 중요한 특징을 추출 가능!
처음에는 2D 이미지지만, 첫 번째 Conv Layer를 거치면 3D 텐서가 됨!
2D 이미지를 CNN에 넣으면, 첫 번째 Convolution Layer를 통과하면서 3차원(3D 텐서)이 생성되기 때문에 이후 연산에서는 3D 텐서를 사용하게 되는 것!
두번째 Pooling Layer
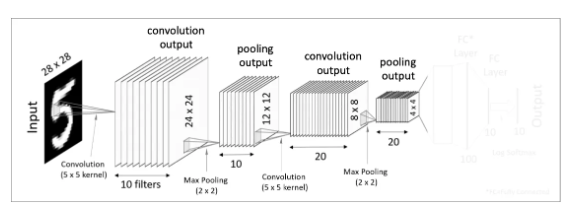
두번째 Pooling layer입니다. 전과 똑같은 방식으로 Pooling과정을 처리해주면 더 크기가 작아진 20개의 4x4 결과값을 얻습니다.
Flatten(Vectorization)
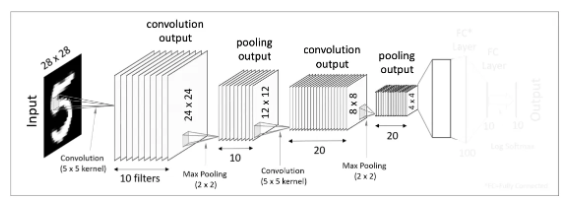
그 후 이 4x4x20의 텐서를 일자 형태의 데이터로 쭉 펼쳐준다고 생각해 봅시다. 이 과정을 Flatten 또는 Vectorization 이라고 합니다. 쉽게 말해 각 세로줄을 일렬로 쭉 세워두는 것입니다. 그러면 이것은 320-dimension을 가진 벡터(vector)형태가 됩니다.
그렇다면 왜 이렇게 1차원 데이터로 변형해도 상관이 없을까요? 이 전에 두번째 pooling layer에서 얻어낸 4x4크기의 이미지들은 이미지 자체라기 보다는 입력된 이미지에서 얻어온 특이점 데이터가 됩니다. 즉 1차원의 벡터 데이터로 변형시켜주어도 무관한 상태가 된다는 의미입니다.
Fully-Connected Layers(Dense Layers)
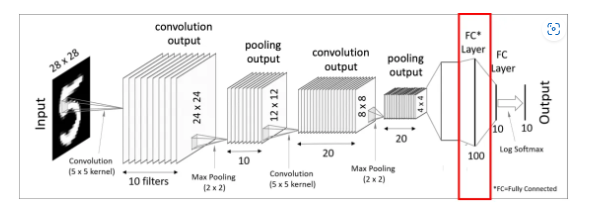
이제 마지막으로 하나 혹은 하나 이상의 Fully-Connected Layer를 적용시키고 마지막에 Softmax activation function을 적용해주면 드디어 최종 결과물을 출력하게 됩니다.
Fully-Connected Layer (FC Layer)란?
CNN에서 마지막 단계에서 Fully-Connected Layer(완전연결층, FC Layer)를 적용하는 이유는
CNN이 추출한 특징(Feature Map)을 바탕으로 최종적으로 분류(Classification) 또는 회귀(Regression)를 수행하기 위해서야!
FC Layer를 하나 또는 여러 개 적용할 때 차이점
FC Layer를 하나만 사용 vs 여러 개 사용?
FC Layer를 하나만 쓰거나 여러 개 쓰는 것은 모델의 복잡도와 학습 효과에 차이를 줌!
FC Layer를 하나만 사용하면?
CNN의 Feature Map을 한 번에 최종 출력층(Softmax)로 변환
모델이 간단해지고 계산량이 적어짐
하지만 복잡한 패턴을 학습하는 능력이 약해질 수 있음
FC Layer를 여러 개 사용하면?
CNN이 학습한 Feature Map을 더 깊게 변형하여 복잡한 패턴을 학습 가능!
비선형성(Non-linearity)을 더 추가하여 모델이 더 강력해짐
하지만 계산량이 증가하고, 과적합(Overfitting) 위험이 있음
즉, FC Layer를 하나만 사용하면 계산량이 줄어들고 빠르게 학습할 수 있지만,
여러 개를 사용하면 더 강력한 학습이 가능하지만 과적합 위험이 있음!
FC Layer에서 Flatten 이후의 과정: 정확한 이해
Flatten을 먼저 해서 1차원 데이터로 변환한 후 FC Layer를 적용하는 것이 맞아.
그런데 FC를 여러 개 쓰더라도 다시 Flatten을 하지 않고,
그냥 1차원 벡터(Flatten된 상태)에서 ReLU를 적용하면서 FC Layer를 여러 번 쌓는 방식으로 진행돼!
CNN에서 Flatten 이후 FC Layer가 수행되는 과정
CNN에서 FC Layer가 적용되는 일반적인 과정
Feature Map(3D 텐서) 생성
CNN의 마지막 Convolution Layer에서 Feature Map이 생성됨
예:
8×8×10 (너비 × 높이 × 채널 수)
Flatten 적용 (1D 벡터로 변환)
8×8×10=640개의 값을 가진 1차원 벡터로 변환
즉, FC Layer에 넣기 위해 3D → 1D 변환
FC Layer 적용 (하나 또는 여러 개)
FC Layer를 하나만 쓰면? → Softmax로 바로 연결
FC Layer를 하나만 사용하면, 기본적으로 Flatten된 데이터를 Softmax로 넘기는 역할만 수행하게 돼.
즉, 추가적인 변형 없이 CNN이 만든 Feature Map을 바로 최종 분류 단계로 넘기는 것!
FC Layer를 여러 개 쓰면? → ReLU 활성화 함수 적용 후 추가적인 FC Layer를 거쳐 Softmax로 연결
즉, FC를 여러 개 쓸 때 다시 Flatten을 반복하는 것이 아니라, 1D 벡터 상태에서 계속 ReLU를 적용하면서 변형을 수행하는 것!
FC Layer를 하나만 쓰는 경우 vs 여러 개 쓰는 경우
FC Layer 하나만 사용하면?
Flatten된 1D 벡터를 바로 Softmax(출력층)로 보냄.
즉, CNN이 추출한 Feature Map을 한 번의 변환만 거쳐 최종 출력을 내놓음.
문제점
Feature Map이 너무 단순한 변환만 거치므로, 복잡한 패턴을 학습하는 능력이 부족할 수 있음.
FC Layer를 여러 개 사용하면?
Flatten된 1D 벡터를 여러 개의 FC Layer를 거쳐 점진적으로 변형한 후 Softmax 적용.
이 과정에서 ReLU 활성화 함수를 적용하여 비선형성을 추가하고, 더욱 강력한 표현력을 갖게 함!
이 과정에서 Flatten을 다시 하지 않음!
Flatten은 처음 한 번만 적용되고, 이후에는 1D 벡터 상태에서 계속 연산이 진행됨.
즉, FC Layer를 여러 개 쓸 때 Flatten을 반복하는 것이 아니라, FC Layer에서 ReLU를 적용하면서 깊이 변형을 수행하는 것!
FC Layer를 너무 많이 사용하면 중요한 데이터가 사라질 수도 있을까?
FC Layer를 너무 많이 쌓으면 오히려 중요한 데이터가 Relu로 인해 0이 되어 정보가 손실될 위험이 있음.
이런 문제를 Dying ReLU 문제 & 과적합(Overfitting) 문제라고 부를 수 있어.
왜 FC Layer를 너무 많이 사용하면 중요한 데이터가 사라질 수 있을까?
(1) Dying ReLU 문제 (죽은 ReLU 문제)
ReLU 함수의 특징:
f(x)=max(0,x)
입력 값이 음수이면 출력이 0이 됨
만약 너무 많은 FC Layer를 쌓고 ReLU를 계속 적용하면, 중요한 정보까지 0으로 변할 위험이 있음!
Dying ReLU 문제 발생 과정
처음에는 CNN이 잘 학습되다가
FC Layer가 너무 많아지면서, ReLU가 계속 적용되다 보면 많은 뉴런들이 0으로 변함.
결국 네트워크가 충분한 정보를 전달하지 못하고, 학습이 제대로 안 됨!
즉, FC Layer를 너무 많이 사용하면 ReLU가 너무 많은 0을 만들어버려서, 중요한 정보까지 날아갈 위험이 있음!
(2) 과적합(Overfitting) 문제
FC Layer가 너무 많으면, 모델이 너무 복잡해져서 과적합될 위험이 있음.
CNN의 Feature Map은 이미 충분히 중요한 특징을 추출했는데,
너무 많은 FC Layer를 거치면서 불필요한 패턴까지 학습할 가능성이 커짐.
결과:
훈련 데이터에서는 성능이 좋지만, 새로운 데이터에서는 성능이 나쁨.
CNN의 원래 목적이 중요한 특징만 추출하는 것인데, FC Layer가 너무 많으면 중요한 특징을 오히려 왜곡할 수 있음!
즉, FC Layer를 너무 많이 사용하면 오버피팅 위험이 커지고, ReLU로 인해 중요한 데이터가 사라질 수도 있음!
FC Layer를 너무 많이 써도 안전하게 학습하는 방법
(1) Leaky ReLU 사용
ReLU 대신 Leaky ReLU를 사용하면 Dying ReLU 문제 해결 가능!
Leaky ReLU는 음수 값도 아주 작은 값(예: 0.01x)으로 남김
즉, 완전히 0이 되는 뉴런이 적어지므로 중요한 정보를 유지할 수 있음!
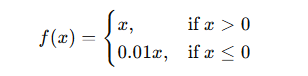
즉, Leaky ReLU를 사용하면 뉴런이 완전히 죽지 않도록 방지할 수 있음!
(2) Dropout 적용 (과적합 방지)
FC Layer가 너무 많으면 모델이 너무 복잡해져서 과적합 위험이 커짐
이를 방지하기 위해 Dropout 기법을 적용
Dropout이란? → 학습 중에 랜덤하게 일부 뉴런을 비활성화(0으로 만듦)하여, 모델이 특정 뉴런에 과도하게 의존하지 않도록 함.
예제: Dropout 50% 적용 시
학습할 때 랜덤하게 절반의 뉴런을 비활성화
FC Layer가 너무 많아도 특정 뉴런만 과도하게 학습되지 않도록 도움
결국 일반화 성능이 좋아지고, 과적합이 방지됨!
즉, Dropout을 사용하면 FC Layer가 너무 많아도 과적합을 방지할 수 있음!
(3) 적절한 FC Layer 개수 선택
CNN에서는 보통 1~2개의 FC Layer만 사용해도 충분함.
너무 깊은 FC Layer를 추가하면 오히려 중요한 데이터가 날아가거나, 과적합될 위험이 있음.
FC Layer는 적절한 개수(1~3개 정도)로 조절하고, 필요할 경우 Dropout을 추가하는 것이 좋음.
예제: 일반적인 CNN 구조
CNN → Feature Map 추출
Flatten
FC Layer (128 노드) + ReLU
FC Layer (64 노드) + ReLU
Softmax 출력층 (10개 노드, MNIST 기준)
즉, FC Layer는 너무 많으면 오히려 문제를 일으킬 수 있으므로, 적절한 개수로 조절해야 함!
FC Layer(완전연결층)를 하나만 사용할 때 vs 여러 개 사용할 때 차이점
FC Layer 하나만 사용하면 왜 복잡한 패턴을 학습하기 어려울까?
FC Layer 하나만 사용하면 단순한 변환만 가능해서 복잡한 패턴을 학습하기 어려움.
CNN의 Feature Map은 이미지에서 특징을 추출한 값이지만,
이를 단 한 번의 FC Layer에서 바로 Softmax로 연결하면 비선형적인 변환이 충분히 이루어지지 않음.
즉, "더 깊게 변형할 기회가 없기 때문에" 복잡한 패턴을 학습하는 능력이 떨어짐.
FC Layer를 여러 개 사용하면 왜 비선형성을 부여할 수 있을까?
FC Layer에서 활성화 함수(예: ReLU)를 사용하면, 입력과 출력 사이의 관계가 단순한 선형 변환이 아니라 비선형 변환이 됨!
즉, 데이터의 복잡한 패턴을 학습할 수 있도록 구조를 확장해 줌!
FC Layer 여러 개를 쌓으면?
첫 번째 FC Layer → 기본적인 변환 수행
두 번째 FC Layer → 첫 번째 Layer의 결과를 더 깊이 변형
세 번째 FC Layer → 더 복잡한 패턴을 학습
즉, FC Layer를 여러 개 사용하면, 각 Layer에서 새로운 비선형성을 추가하면서 데이터의 패턴을 점진적으로 복잡하게 변형할 수 있음!
예제: 숫자(0~9) 이미지 분류 문제에서 FC Layer 개수에 따른 차이
Case 1: FC Layer 하나만 사용
CNN이 Feature Map을 추출 → Flatten (1D 벡터로 변환)
바로 Softmax 출력층으로 연결 → 숫자 0~9 중 하나 예측
비선형 변환을 한 번만 수행하기 때문에 복잡한 특징을 학습하기 어려움.
결과:
단순한 패턴만 학습 가능
깊은 패턴을 학습하지 못해 성능이 낮을 가능성이 큼
Case 2: FC Layer 여러 개 사용
CNN이 Feature Map을 추출 → Flatten
첫 번째 FC Layer → 활성화 함수 (ReLU) 적용 → 비선형성 추가
두 번째 FC Layer → 더 깊은 비선형 변환 수행
마지막 FC Layer → Softmax 출력층 연결
결과:
깊은 구조를 통해 복잡한 패턴 학습 가능
비선형 변환을 여러 번 거쳐 더 강력한 모델이 됨!
즉, FC Layer를 여러 개 사용하면, 여러 번 비선형 변환을 수행하면서 복잡한 패턴을 더 잘 학습할 수 있음!
FC Layer는 뭘 Output(출력) 하는가?
CNN의 마지막 Fully-Connected Layer는 출력층(Output Layer)로 연결되어 최종 예측값을 출력!
FC Layer는 CNN이 학습한 Feature Map을 기반으로 "최종적인 결론"을 도출하는 역할!
이 출력값은 분류(Classification) 또는 회귀(Regression)에 따라 다르게 해석됨
분류(Classification) 문제에서 FC Layer의 출력
예: 고양이 🐱 vs 개 🐶 분류 (이진 분류, Binary Classification)
마지막 FC Layer에서 2개의 출력값을 생성 → 고양이일 확률 vs 개일 확률
Softmax를 적용하면 확률값(예: [0.9, 0.1])이 나오고, 확률이 높은 클래스를 선택!
다중 클래스 분류(Multi-class Classification) 문제에서 FC Layer의 출력
예: 숫자 손글씨 인식 (MNIST, 0~9 숫자 분류)
마지막 FC Layer에서 10개의 출력값 생성 (0~9 각각에 대한 점수)
Softmax를 적용하여 가장 높은 확률을 가진 숫자를 최종 예측!
회귀(Regression) 문제에서 FC Layer의 출력
예: 집값 예측 문제
마지막 FC Layer에서 단 하나의 연속적인 값(예: 305,000달러)을 출력!
Softmax를 사용하지 않고, Linear Activation(선형 활성화)로 그대로 출력
즉, FC Layer는 CNN이 학습한 Feature Map을 기반으로 최종 예측값을 생성하는 역할!
FC Layer의 출력과 Softmax의 관계
FC Layer는 최종적인 숫자 벡터(logits)를 출력함.
Softmax 활성화 함수를 적용하면 출력값이 확률(0~1)로 변환됨.
모델이 가장 확률이 높은 클래스를 최종 예측값으로 선택!
예제: 숫자 손글씨 인식 (0~9)
원래 FC Layer 출력(Logits) Softmax 적용 후(확률)
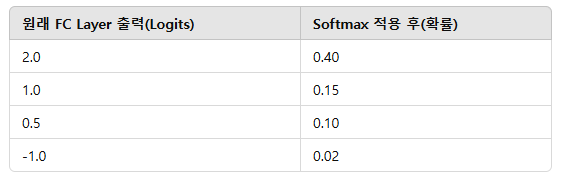
Softmax를 사용하면 CNN이 최종적으로 "이 데이터는 어떤 클래스인가?"를 결정할 수 있음!
- 매개변수(Parameter)와 Hyper-매개변수(Hyper-parameter)
우선 Parameter와 Hyper-parameter, 용어 정리부터 해보도록 하겠습니다
모델 매개변수(parameter)는 모델 내부에 있으며 데이터로부터 값이 추정될 수 있는 설정변수(configuration variable)입니다.
모델 하이퍼파라미터(hyper-parameter)는 모델 외부에 있으며 데이터로부터 값이 추정될 수 없는 설정변수 입니다.
딥러닝의 기본은 파라미터들을 최적의 값으로 빠르고 정확하게 수렴하는 것을 목적으로 합니다. 때문에 어떻게 모델의 파라미터들을 최적화 시키냐 하는 것은 모델 트레이닝의 중요한 포인트입니다.
모델을 학습시킬때 좋은 하이퍼파라미터를 찾는 것 또한 중요합니다. 이것을 ‘하이퍼파라미터를 튜닝한다(tune haperparameters)’고 표현합니다.
매개변수(Parameter)란?
매개변수(Parameter)는 모델 내부에서 학습되는 값(Weight & Bias)!
데이터를 기반으로 최적의 값이 자동으로 찾아지는 값
모델 학습 과정에서 변화하면서 최적의 값으로 조정됨
모델이 "이 값들을 조정하면서 학습하는 것"이 딥러닝의 핵심!
CNN의 예제:
가중치(Weights, 𝑊) → 필터(커널)의 값
편향(Bias, 𝑏) → 각 뉴런이 학습하는 추가적인 값
매개변수(Parameter)의 특징
모델 내부에 존재함
훈련 데이터에 의해 학습됨 (즉, 자동으로 업데이트됨)
Gradient Descent(경사 하강법) 같은 최적화 알고리즘으로 업데이트됨
즉, Parameter는 "모델이 학습하면서 조정하는 값"이다!
하이퍼매개변수(Hyper-parameter)란?
하이퍼매개변수(Hyper-parameter)는 모델의 학습을 조정하는 설정 값!
훈련 과정에서 학습되지 않고, 사람이 직접 설정하는 값
좋은 하이퍼파라미터를 찾는 것이 모델 성능에 큰 영향을 줌
이 값을 튜닝하는 과정이 "하이퍼파라미터 튜닝(Tuning)"
CNN의 예제:
학습률(Learning Rate, 𝛼) → 가중치를 얼마나 빠르게 업데이트할지 결정
배치 크기(Batch Size) → 한 번에 몇 개의 데이터를 학습할지 결정
에포크(Epoch) → 전체 데이터를 몇 번 반복해서 학습할지
필터 크기(Filter Size) → Convolution Layer에서 사용하는 커널 크기
레이어 개수(Layers) → CNN에 몇 개의 레이어를 넣을지
하이퍼매개변수(Hyper-parameter)의 특징
모델 외부에서 설정됨
훈련 데이터에 의해 자동으로 조정되지 않음 (사람이 직접 설정해야 함!)
좋은 값을 찾는 것이 모델 성능을 높이는 핵심 요소!
즉, Hyper-parameter는 "모델 학습을 조정하는 설정 값"이다!
하이퍼파라미터 튜닝(Tuning)이 중요한 이유
좋은 Hyper-parameter를 설정하면 모델의 성능이 크게 향상됨!
학습률이 너무 크면? → 모델이 최적값을 찾지 못하고 발산할 수 있음.
학습률이 너무 작으면? → 학습이 너무 느려지고 최적값을 찾기 어려울 수 있음.
배치 크기가 너무 작으면? → 학습이 불안정할 수 있음.
배치 크기가 너무 크면? → 모델이 일반화 성능이 떨어질 수 있음.
즉, 하이퍼파라미터를 잘 튜닝하는 것이 좋은 모델을 만드는 핵심 요소!
학습 가능한 매개변수의 수
이제 우리가 아까 살펴본 CNN 모델의 학습 가능한 매개변수(trainable parameters)는 몇개나 되는지 살펴봅시다.
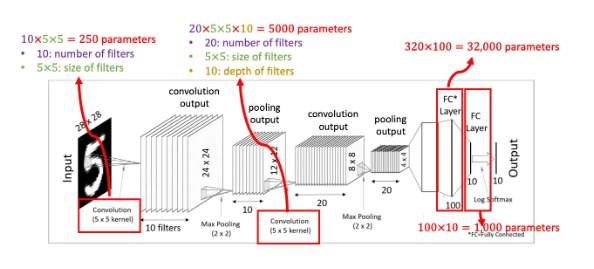
첫 convolution과정에서 5x5크기의 필터 10개를 사용하였으므로 250개의 매개변수가 존재합니다.
Pooling layer에서는 단순히 크기를 줄이는 개념이므로 매개변수가 없습니다.
두번째 convolution 과정에서 5x5x10 크기의 텐서 20개를 사용하였으므로 5,000개의 매개변수가 추가되었습니다
두개의 Fully-connected layer들에서 각각 매개변수 32,000개, 1000개가 추가되었습니다.
4 X 4 X 20 = 320(FC의 input) X 100(FC의 output) = 32,000
100 X 10 = 1000
FC layer에서 320 -> 100 -> 10 으로 데이터를 줄임
결과적으로, 생략한 intercepts 값까지 고려해보면 총 38,250 이상의 학습 가능한 매개변수를 갖게 됩니다.
FC Layer에서 최종 뉴런 개수를 줄이는 원리 (이진 분류 vs 다중 분류)
CNN에서 마지막 FC Layer의 뉴런 개수는 "분류할 클래스 개수"와 동일하게 설정돼.
즉, 0~9 숫자 분류라면 10개, 이진 분류(Binary Classification)라면 2개!
마지막 FC Layer에서 뉴런 개수를 줄이는 이유
CNN이 Feature Map에서 특징을 추출한 후, 최종적으로 출력층(Output Layer)에서 분류 작업을 수행
이때 출력 뉴런의 개수 = 클래스 개수로 설정됨!
이렇게 하면 Softmax(또는 Sigmoid)를 적용하여 확률을 출력할 수 있음.
다중 분류(Multi-class Classification) → 출력 뉴런 개수 = 클래스 개수
예제: 숫자 인식 (0~9까지 총 10개 클래스)
FC Layer의 마지막 출력 뉴런 개수를 10개로 설정
Softmax 활성화 함수 적용 → 각 숫자(클래스)에 대한 확률을 출력
가장 확률이 높은 클래스를 최종 예측값으로 사용
즉, 다중 분류에서는 FC Layer의 마지막 뉴런 개수를 "클래스 개수"로 설정하고, Softmax를 적용함!
이진 분류(Binary Classification) → 출력 뉴런 개수 = 2개 또는 1개
이진 분류(Binary Classification)에서는 두 가지 방법이 있음!
(1) 출력 뉴런을 2개로 설정하고 Softmax 적용
예제: 개 🐶 vs 고양이 🐱 분류 (2개 클래스)
마지막 FC Layer에서 뉴런 개수를 2개로 설정!
Softmax를 적용하면 각 클래스에 대한 확률이 나옴.
확률이 더 높은 클래스를 예측값으로 선택
이진 분류에서는 일반적으로 뉴런을 1개만 사용하고 Sigmoid를 적용하는 방식을 더 많이 씀!
2) 출력 뉴런을 1개로 설정하고 Sigmoid 적용
예제: 스팸 메일(1) vs 정상 메일(0) 분류 (Binary Classification)
마지막 FC Layer에서 뉴런 개수를 1개로 설정!
Sigmoid 활성화 함수 적용 → 0~1 사이의 확률을 출력
Sigmoid 출력값 (이진 분류)
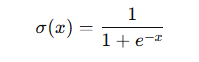
예제 결과:
0.9 이상이면 "스팸" (1)
0.1 이하이면 "정상 메일" (0)
즉, 이진 분류에서는 보통 출력 뉴런을 1개로 설정하고, Sigmoid 활성화 함수를 적용함!
입력 (28×28 이미지)
첫 번째 Convolution Layer (5×5 필터 10개 사용) → 250개 매개변수
Pooling Layer (2×2 Max Pooling, 차원 축소)
두 번째 Convolution Layer (5×5×10 필터 20개 사용) → 5000개 매개변수
Pooling Layer (2×2 Max Pooling, 다시 차원 축소)
Flatten (CNN의 Feature Map을 1D 벡터로 변환, 320 뉴런)
FC Layer 1: 320 → 100 (뉴런 개수 감소) → 32,000개 매개변수
FC Layer 2: 100 → 10 (Softmax 출력층) → 1000개 매개변수
즉, CNN이 Feature를 추출한 후, FC Layer에서 점진적으로 뉴런 개수를 줄이는 구조!
FC Layer에서 320 → 100으로 줄이는 이유
왜 320개 뉴런을 그대로 사용하지 않고 100개로 줄이는 걸까?
(1) 계산량을 줄이기 위해 (컴퓨팅 비용 감소)
320개 뉴런을 그대로 유지하면 계산량이 너무 많아짐.
FC Layer는 모든 뉴런이 서로 연결되므로, 뉴런 개수가 많을수록 파라미터(가중치)도 급격히 증가!
예를 들어, 뉴런 개수를 줄이지 않고 320 → 1000으로 바로 연결하면?
320×1000=320,000(매개변수)
하지만 뉴런 개수를 320 → 100으로 줄이면?
320×100=32,000(매개변수)
즉, 뉴런 개수를 줄이면 FC Layer의 계산량이 감소하고 학습 속도가 빨라짐!
(2) 과적합 방지 (Overfitting Prevention)
뉴런이 너무 많으면 모델이 훈련 데이터에 과도하게 맞춰질 가능성(과적합)이 커짐.
FC Layer에서 뉴런 개수를 점진적으로 줄이면 불필요한 패턴(Noise)을 제거하고 일반화 성능이 향상됨.
즉, 새로운 데이터에서도 더 잘 작동하는 모델을 만들 수 있음!
(3) 중요한 특징만 유지 (Feature Selection & Compression)
CNN이 추출한 Feature Map(320 뉴런)에는 중요한 특징 + 불필요한 정보가 섞여 있음.
FC Layer에서 뉴런 개수를 줄이면 가장 중요한 정보만 남기고, 불필요한 데이터는 제거할 수 있음.
즉, 중요한 특징을 압축하는 역할 (Feature Compression)!
즉, 320 → 100으로 뉴런 개수를 줄이면 계산량이 줄어들고, 과적합을 방지하면서, 중요한 특징만 남길 수 있음!
마지막 FC Layer에서는 100개 뉴런을 10개로 줄여서 Softmax를 적용
10개의 뉴런은 0~9까지 숫자를 분류하는 클래스 (MNIST 같은 데이터셋)
Softmax를 적용하면 각 숫자(클래스)에 대한 확률 값이 출력됨
가장 확률이 높은 클래스를 최종 예측값으로 사용!
FC Layer의 매개변수(Parameter)란?
매개변수(Parameter)란 모델이 학습하는 값(가중치 & 편향)
FC Layer에서는 입력 뉴런(Input)과 출력 뉴런(Output) 사이에 가중치(Weight)가 연결됨.
또한, 각 뉴런마다 편향(Bias)도 존재함.
FC Layer의 매개변수 개수는 (입력 뉴런 수 × 출력 뉴런 수) + 편향 뉴런 수로 계산됨.
예제: FC Layer에서 매개변수 개수 계산
입력 뉴런 개수: 128
출력 뉴런 개수: 256
가중치(Weights) 개수 = 128 × 256 = 32,768
편향(Bias) 개수 = 256
총 매개변수 개수 = 32,768 + 256 = 33,024
즉, FC Layer에서 매개변수는 "입력 뉴런 × 출력 뉴런 + 편향"으로 계산됨!
Intercepts 값(편향, Bias)이란?
Intercepts(Bias)란? 뉴런이 학습할 때 추가적인 조정을 해주는 값
모든 뉴런에는 편향(Bias, b) 값이 추가됨.
편향은 입력 값이 0일 때도 뉴런이 활성화될 수 있도록 도와줌!
왜 편향이 필요할까?
만약 Bias가 없으면?
입력값이 0이면 뉴런도 항상 0이 되어 학습이 어려울 수 있음.
Bias를 추가하면?
입력값이 0이어도 뉴런이 활성화될 수 있음 → 학습이 더 유연해짐.
즉, Bias는 뉴런이 더 효과적으로 학습할 수 있도록 돕는 추가적인 조정 값!
가중치(Weight)란?
가중치(Weight)는 입력 값이 출력에 미치는 영향을 조절하는 값이야.
각 뉴런은 입력 값과 연결된 가중치(Weight)를 곱한 후 더해서 출력을 결정함.
가중치가 크면 해당 입력 값이 결과에 큰 영향을 미침.
가중치가 작거나 0에 가까우면 해당 입력 값의 영향이 줄어듦.
뉴런에서 가중치가 적용되는 과정
y=W⋅x+b
여기서 𝑊는 가중치(Weight), 𝑏는 편향(Bias), 𝑥는 입력 값
즉, 가중치는 입력이 결과에 얼마나 중요한지를 결정하는 학습 가능한 변수!
편향(Bias)란?
편향(Bias)는 입력 값이 0일 때도 뉴런이 일정한 출력을 가질 수 있도록 조정하는 값이야.
뉴런의 출력이 항상 입력 값(Weight X Input)에만 의존하면 학습이 제한적이 될 수 있음.
따라서 편향(Bias)을 추가하면, 뉴런이 더 유연한 표현력을 가질 수 있음.
편향이 적용되는 방식
y=W⋅x+b
𝑏(Bias)가 입력 값이 0일 때도 뉴런이 활성화될 수 있도록 도와줌.
즉, 편향은 뉴런이 학습할 때 더 유연하게 작동하도록 해주는 중요한 역할을 함!
편향의 개수는 무조건 출력 뉴런 개수와 동일한가?
편향의 개수는 무조건 출력 뉴런의 개수와 동일함.
왜 그런가?
각 뉴런은 하나의 출력 값을 가짐.
따라서 각 뉴런이 독립적으로 학습하기 위해, 각 뉴런마다 하나의 편향 값이 필요함.
즉, 편향은 각 출력 뉴런마다 하나씩 존재해야 하므로, 항상 출력 뉴런 개수와 동일함!
가중치(Weight)와 편향(Bias)는 자동으로 설정되는가?
가중치(Weight)와 편향(Bias)는 손실 함수(Loss Function)와 최적화 알고리즘(Optimizer)이 자동으로 조정(학습)해줌
가중치와 편향을 직접 설정하지 않는 이유
가중치와 편향은 모델이 학습하면서 최적의 값으로 업데이트됨.
손실 함수(Loss Function)가 현재 모델이 얼마나 잘 예측하는지 평가함.
최적화 알고리즘(Optimizer, 예: SGD, Adam)이 가중치와 편향을 업데이트함.
즉, 우리가 해야 할 일은 손실 함수와 최적화 알고리즘을 잘 선택하는 것뿐!
가중치와 편향은 우리가 직접 수정할 필요 없이 모델이 알아서 최적화해줌.
초매개변수(Hyper-parameters)
마지막으로 CNN모델에서 튜닝 가능한 하이퍼파라미터는 어떤 것들이 있는지 간단히 살펴보겠습니다.
Convolutional layers: 필터의 갯수, 필터의 크기, stride값, zero-padding의 유무
Pooling layers: Pooling방식 선택(MaxPool or AvgPool), Pool의 크기, Pool stride 값(overlapping)
Fully-connected layers: 넓이(width)
활성함수(Activation function): ReLU(가장 주로 사용되는 함수), SoftMax(multi class classification), Sigmoid(binary classification)
Loss function: Cross-entropy for classification, L1 or L2 for regression
최적화(Optimization) 알고리즘과 이것에 대한 hyperparameter(보통 learning rate): SGD(Stochastic gradient descent), SGD with momentum, AdaGrad, RMSprop
Random initialization: Gaussian or uniform, Scaling
CNN 모델에서 튜닝 가능한 하이퍼파라미터(Hyper-parameters)
CNN 모델에서 성능을 최적화하려면 하이퍼파라미터(Hyper-parameters)를 적절히 튜닝해야 해.
Convolutional Layers의 하이퍼파라미터
합성곱 레이어(Convolutional Layer)에서 조정할 수 있는 주요 하이퍼파라미터
(1) 필터의 개수 (Number of Filters)
필터(커널) 개수는 특징(Feature)을 얼마나 잘 추출할지 결정하는 요소
필터 개수가 많을수록 더 다양한 패턴을 학습할 수 있지만, 계산량이 증가함.
보통 처음 레이어에서는 적은 개수(32 or 64), 깊은 레이어에서는 더 많은 개수(128 or 512) 사용
(2) 필터 크기 (Kernel Size)
필터의 크기는 이미지의 작은 패턴(특징)을 얼마나 정밀하게 포착할지를 결정
가장 일반적인 크기:
3×3 또는 5×5
작은 필터(3×3) → 세밀한 특징을 학습
큰 필터(5×5 이상) → 더 넓은 영역에서 특징을 학습하지만, 세밀한 특징을 놓칠 수도 있음
(3) Stride 값
필터가 한 번 이동할 때 몇 칸씩 이동하는지를 결정
기본값: stride=1
Stride 값이 크면 → 연산량 감소 (하지만 정보 손실 가능)
Stride 값이 작으면 → 연산량 증가 (더 정밀한 특징 추출 가능)
(4) Zero-padding 여부
합성곱 연산 시 이미지 크기가 줄어드는 문제를 방지하기 위해 가장자리(padding)에 0을 추가
same: Zero-padding을 사용하여 입력과 출력 크기를 동일하게 유지
valid: Zero-padding 없이 원래 방식으로 연산 (출력 크기가 작아짐)
즉, Zero-padding을 사용하면 정보 손실 없이 원본 크기를 유지할 수 있음!
Pooling Layers의 하이퍼파라미터
Pooling Layer는 이미지 크기를 줄이고, 중요한 특징만 유지하는 역할을 함.
(1) Pooling 방식 선택 (MaxPooling vs AvgPooling)
Max Pooling → 가장 널리 사용됨!
특정 영역에서 가장 큰 값을 선택 (주요 특징만 유지)
텍스처나 윤곽선을 강조하는 데 효과적
Average Pooling
특정 영역에서 평균 값을 선택 (부드러운 특징 유지)
배경이 중요한 이미지 분석에서 사용됨
(2) Pool 크기 (Pool Size)
Pooling 크기를 키우면 더 많은 정보를 압축할 수 있지만, 너무 크면 중요한 정보가 사라질 수 있음.
보통 2×2 또는 3×3을 사용
pool_size=(2,2)이면 출력 크기가 절반으로 줄어듦.
(3) Pool Stride 값
stride는 Pooling 연산이 한 번에 몇 칸씩 이동할지 결정
기본값: stride = pool_size
Stride를 Pool 크기보다 작게 설정하면 겹치는 Pooling(Overlapping Pooling)이 발생할 수도 있음.
즉, Pooling은 크기를 줄이면서도 중요한 특징을 유지하는 역할을 함!
Fully-Connected Layers의 하이퍼파라미터
FC Layer는 CNN이 추출한 특징을 바탕으로 최종적인 분류를 수행하는 단계!
(1) 뉴런 개수 (Width)
뉴런 개수(Width)가 많을수록 모델의 표현력이 증가하지만, 과적합 가능성도 커짐.
보통 Dense(512) → Dense(256) → Dense(10) 같은 방식으로 점진적으로 줄임.
즉, FC Layer에서는 적절한 뉴런 개수를 설정하여 모델이 잘 학습하도록 튜닝해야 함!
활성화 함수 (Activation Function)
활성화 함수는 뉴런이 출력하는 값을 변형하여 학습을 돕는 역할을 함.
주요 활성화 함수
ReLU (Rectified Linear Unit)
가장 많이 사용되는 활성화 함수
음수 값은 0으로 변환하고, 양수 값은 그대로 유지
max(0, x)
Sigmoid
이진 분류(Binary Classification)에 사용됨
출력이 항상 0~1 사이의 확률 값을 가짐.
σ(x) = 1 / (1 + e^-x)
Softmax
다중 클래스 분류(Multi-class Classification)에 사용됨
모든 출력 값의 합이 1이 되도록 변환
즉, ReLU는 기본적으로 사용하고, 분류 방식에 따라 Sigmoid 또는 Softmax를 선택!
최적화 알고리즘과 관련 하이퍼파라미터
최적화 알고리즘(Optimizer)은 가중치를 업데이트하는 방식을 결정함.
SGD (Stochastic Gradient Descent)
기본적인 경사 하강법
학습률(Learning Rate)이 중요함
Adam (Adaptive Moment Estimation)
가장 널리 사용되는 최적화 알고리즘!
학습률을 자동으로 조정해줌.
즉, 대부분의 경우 Adam이 기본적으로 사용됨!
손실 함수 (Loss Function)
손실 함수(Loss Function)는 모델이 예측한 값과 실제 값의 차이를 계산하는 함수
손실 함수가 작을수록 모델이 더 잘 예측하고 있다는 의미
CNN에서는 분류(Classification)와 회귀(Regression)에 따라 다른 손실 함수를 사용
(1) 분류(Classification) 손실 함수
Cross-Entropy (교차 엔트로피)
분류 문제에서는 크로스 엔트로피(Cross-Entropy)를 사용
모델이 예측한 확률 분포가 실제 정답과 얼마나 차이나는지를 측정
이진 분류(Binary Classification) → Binary Cross-Entropy
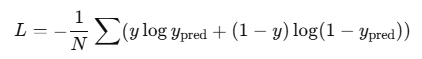
다중 클래스 분류(Multi-class Classification) → Categorical Cross-Entropy
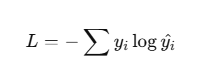
즉, CNN이 분류 문제를 풀 때는 Cross-Entropy 손실 함수를 사용!
(2) 회귀(Regression) 손실 함수
L1 손실 (Mean Absolute Error, MAE)
절대 오차(Absolute Error)를 사용하여 손실을 계산
이상치(Outlier)에 강함
L2 손실 (Mean Squared Error, MSE)
제곱 오차(Squared Error)를 사용하여 손실을 계산
이상치에 민감함
즉, CNN이 회귀 문제를 풀 때는 L1(MAE) 또는 L2(MSE) 손실 함수를 사용!
최적화 알고리즘 (Optimization Algorithm)
최적화 알고리즘은 손실 함수를 최소화하기 위해 가중치(Weight)와 편향(Bias)를 업데이트하는 방법
CNN에서는 대표적으로 SGD, Adam, RMSprop 같은 최적화 알고리즘을 사용
(1) SGD (Stochastic Gradient Descent, 확률적 경사 하강법)
가장 기본적인 경사 하강법(Gradient Descent)
랜덤으로 일부 샘플을 선택하여 가중치를 업데이트
학습률(Learning Rate)을 잘 조정해야 함
즉, SGD는 기본적인 경사 하강법으로, 학습률 조정이 매우 중요함!
(2) SGD with Momentum
일반적인 SGD보다 더 빠르게 수렴하도록 Momentum(관성 효과)을 추가한 버전
이전 업데이트 방향을 일정 부분 유지하여 진동(oscillation)을 줄이고 빠르게 최적값을 찾음
즉, Momentum을 추가하면 학습이 더 안정적이고 빠르게 진행됨!
(3) AdaGrad (Adaptive Gradient)
가중치를 업데이트할 때 각 변수마다 다른 학습률을 적용
자주 업데이트되는 가중치의 학습률은 줄이고, 드물게 업데이트되는 가중치는 학습률을 증가시킴
즉, AdaGrad는 학습률을 자동으로 조정하여 일부 가중치가 너무 빨리 줄어드는 문제를 방지함!
(4) RMSprop (Root Mean Square Propagation)
AdaGrad의 단점을 보완한 알고리즘
최근 기울기 변화량을 고려하여 학습률을 조정
CNN에서 널리 사용됨!
즉, RMSprop은 CNN에서 기본적으로 많이 사용되는 최적화 알고리즘!
(5) Adam (Adaptive Moment Estimation)
SGD + Momentum + RMSprop을 결합한 방식
학습률을 자동으로 조절하여 가장 효과적으로 학습
현재 가장 많이 사용되는 최적화 알고리즘!
즉, Adam은 학습률 조정이 자동으로 이루어져 가장 안정적인 최적화 알고리즘!
가중치 초기화 방법 (Random Initialization)
가중치 초기화(Weight Initialization)는 모델의 학습 성능을 좌우하는 중요한 요소!
가중치를 너무 작거나 크게 초기화하면 학습이 어려워짐
(1) Gaussian 초기화
정규 분포를 따라 가중치를 초기화
평균이 0, 표준편차가 작은 값으로 설정
일반적인 뉴럴 네트워크에서 사용됨
(2) Uniform 초기화
균등 분포에서 랜덤한 값을 선택하여 초기화
값이 너무 작거나 크면 학습이 느려질 수 있음
(3) Xavier(Glorot) 초기화
입력 뉴런과 출력 뉴런의 개수에 따라 가중치를 초기화
활성화 함수가 Sigmoid, Tanh일 때 적절함
(4) He 초기화
ReLU 계열 활성화 함수에 적합한 초기화 방법
가중치를 더 크게 설정하여 학습 속도를 높이고, 기울기 소실(Vanishing Gradient) 문제를 해결
즉, CNN에서는 He 초기화가 가장 많이 사용됨!