외적(Cross Products)

외적이란?

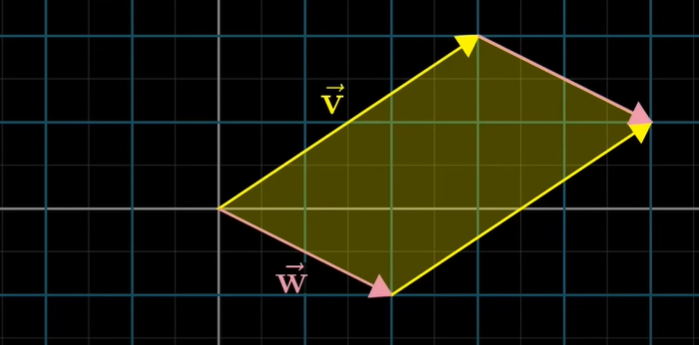
2차원에서 외적은 두 벡터로 만들어지는 평행사변형의 넓이를 뜻한다. 중요한 것은 외적은 내적과 달리 스칼라 값을 반환하는 것이 아니라 벡터를 반환한다는 것이다!! $\overrightarrow{v}$와 $\overrightarrow{w}$의 외적은 $\overrightarrow{v} \times \overrightarrow{w}$로 표기한다.

외적에는 방향에 대한 정보도 갖는다. 외적하는 벡터의 순서에 따라 부호가 달라진다.

• $\overrightarrow{v}$가 $\overrightarrow{w}$ 오른쪽에 있는 경우 양수
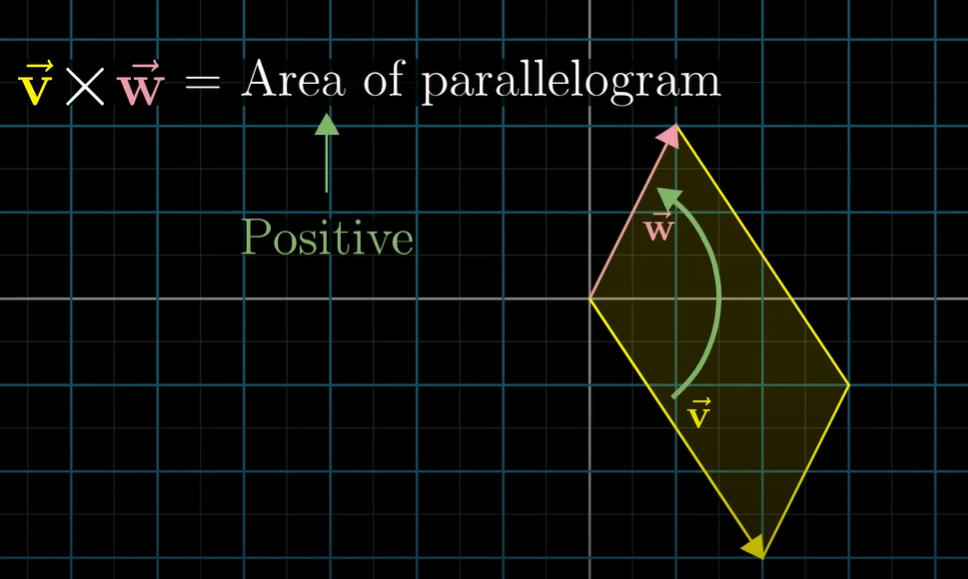
• $\overrightarrow{v}$가 $\overrightarrow{w}$ 왼쪽에 있는 경우 음수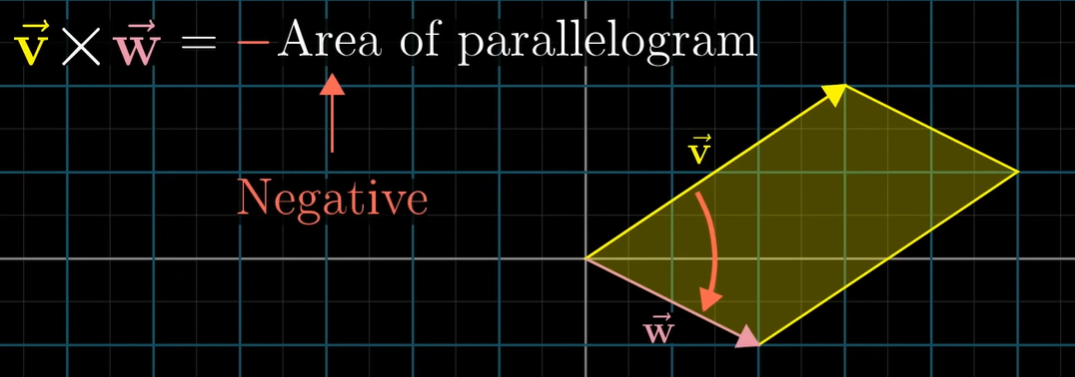따라서 아래 식이 성립한다.
  $\overrightarrow{v} \times \overrightarrow{w} = -\overrightarrow{w} \times \overrightarrow{v}$

평행사변형의 면적을 계산하기 위해서 행렬식을 이용하면 된다.

왜냐하면 행렬식은 공간이 얼마나 확대/축소 되는지를 나타내는 것이다.(6강 참고) 따라서 원래 공간($\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$) 대비 $\overrightarrow{v}$와 $\overrightarrow{w}$를 기저벡터로 삼는 공간은 얼마나 확대/축소 되었는지 판단할 수 있기 때문이다. 중요한 것은 $\overrightarrow{v}$와 $\overrightarrow{w}$가 선형변환한 공간의 기저벡터로 사용된다는 것이다.

2차원에서 외적의 성질

외적은 아래와 같은 성질을 갖는다.

• 평행사변형은 두 벡터가 직교할 때 가장 크다. 왜냐하면 평행사변형의 넓이는 정사각형에 가까울 수록 넓이가 커지기 때문이다.
• 한 벡터를 스케일링하면 외적의 결과도 동일한 비율로 스케일링 된다. 평행사변형의 면적이기 때문에 밑변(혹은 높이)가 커지는 만큼 면적도 넓어지기 때문이다.

3차원에서의 외적

3차원으로 바뀌어도 외적의 결과로 벡터가 반환된다는 것은 변하지 않는다.(어쩌면 3차원에서 보는 외적이 2차원에서 보는 외적보다 더 정확한 의미를 나타낼 지도 모르겠다.)

3차원에서의 외적은 두 벡터를 결합하여 새로운 벡토를 만들어 내는일이다. 새로운 벡터는 아래와 같은 힘과 방향을 갖는다.

• 새로운 벡터의 길이 : 두 벡터가 만들어내는 평행사변형의 넓이
• 새로운 벡터의 방향 : 두 벡터가 만들어내는 평행사변형과 수직 방향
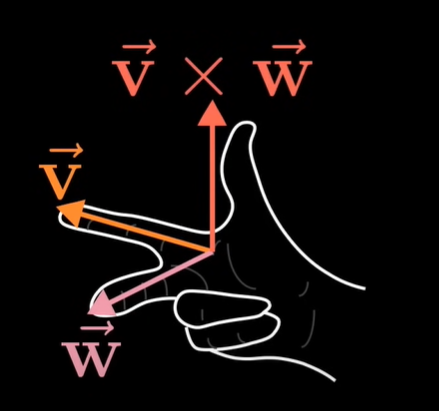
  • 새로운 벡터가 만들어지는 방향은 오른손 법칙을 상용하여 평행사변형 위쪽에 만들어지는지, 평행사변형 아래에 만들어지는지 정해진다.(아래 그림 참고)
    

3차원에서 외적을 구하는 방법은 아래와 같다.

위 공식에서 조금 이상한 것은 첫 번째 열에 기저벡터를 넣는다는 것이다. 이것은 계산을 위해 표기만 빌린 것이므로 실제 행렬의 의미는 아니다! 위 공식을 통해 $\overrightarrow{v}$와 $\overrightarrow{w}$가 만드는 평행사변형의 넓이를 길이로 가지면서 평행사변형과 수직인 벡터식을 구할 수 있다.($\hat{i}, \hat{j}, \hat{k}$가 모두 3차원이므로 결과도 3차원 벡터로 나옴)

※ 다음 강의(11강)은 위 내용의 심화 내용이므로 정리 x