내적(dot product)
두 개의 벡터를 내적하는 것은 어떤 의미일까?
수치적인 접근
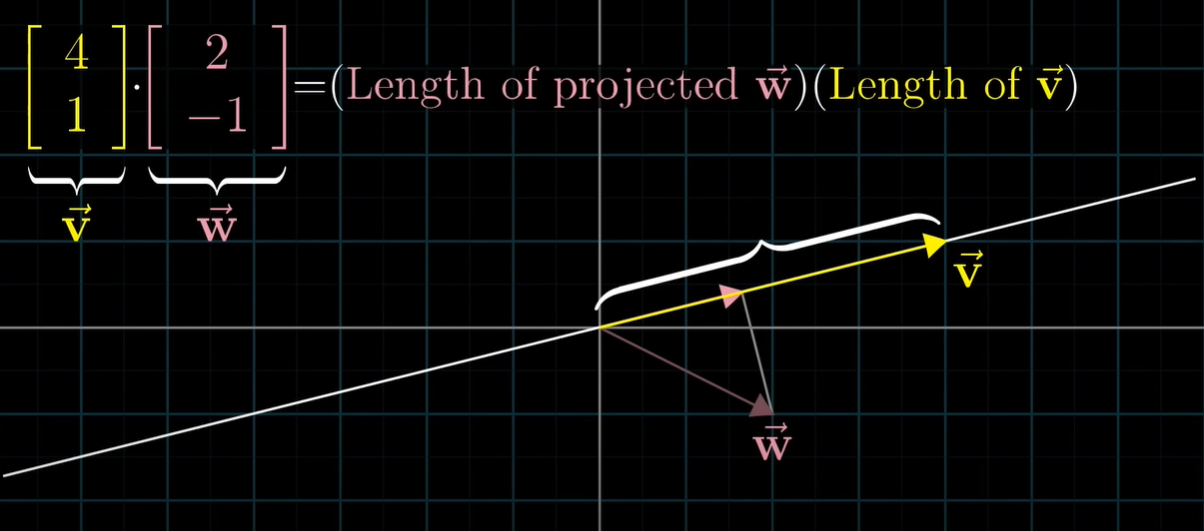
v → = [ 1 2 ] , w → = [ 3 4 ] v → • w → = [ 1 × 3 2 × 4 ] = [ 3 8 ] \overrightarrow{v}= \begin{bmatrix} 1 \\ 2 \end{bmatrix}, \overrightarrow{w} = \begin{bmatrix} 3\\4 \end{bmatrix} \\ \overrightarrow{v} • \overrightarrow{w} = \begin{bmatrix} 1 \times 3 \\ 2 \times 4 \end{bmatrix} = \begin{bmatrix} 3 \\ 8 \end{bmatrix} v = [ 1 2 ] , w = [ 3 4 ] v • w = [ 1 × 3 2 × 4 ] = [ 3 8 ] 두 벡터의 내적은 그냥 각 자리수를 맞춰서 두 수를 곱하면 된다. 그렇다면 왜 이렇게 연산이 될까?
기하학적인 접근
기하학적인 측면에서 두 벡터의 내적은 하나의 벡터를 다른 벡터에 투영(projection)하고 투영한 벡터의 길이와 다른 벡터의 길이를 곱하면 된다. (아래 그림 참고)
내적 결과의 부호는 두 벡터의 방향에 따라 결정된다.
w → \overrightarrow{w} w v → \overrightarrow{v} v w → \overrightarrow{w} w v → \overrightarrow{v} v w → \overrightarrow{w} w v → \overrightarrow{v} v w → \overrightarrow{w} w v → \overrightarrow{v} v
그렇다면, 어떻게 수치적인 접근과 기하학적인 접근이 같을까? 둘 사이에는 어떤 관계가 있는 것일까?
2차원을 1차원으로 축소하기
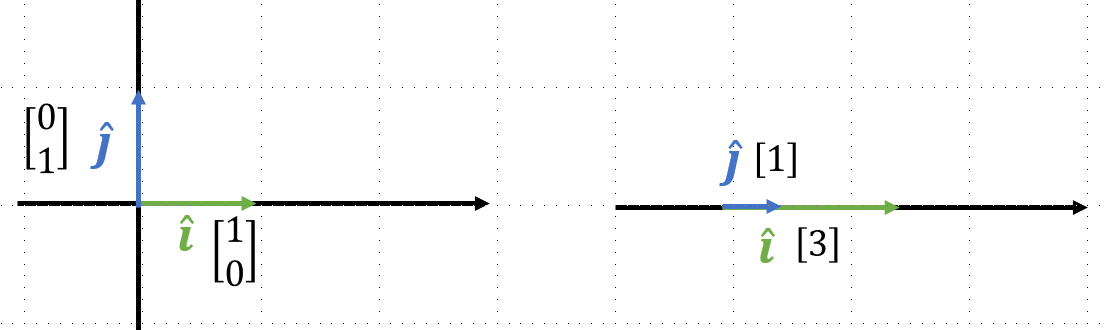
2차원을 1차원으로 축소하면 하면 아래와 같이 벡터는 하나의 숫자로 표현이 가능하다. 아래 예시를 보면, 원래는 [ 1 0 ] T \begin{bmatrix} 1 & 0 \end{bmatrix}^T [ 1 0 ] T [ 0 1 ] T \begin{bmatrix} 0 & 1 \end{bmatrix}^T [ 0 1 ] T [ 3 ] \begin{bmatrix} 3 \end{bmatrix} [ 3 ] [ 1 ] \begin{bmatrix} 1\end{bmatrix} [ 1 ]
[ 1 0 0 1 ] → [ 3 1 ] \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} \overrightarrow{} \begin{bmatrix}3 & 1 \end{bmatrix} [ 1 0 0 1 ] [ 3 1 ] 1차원으로 차원이 축소 되더라도 그 공간에 있는 벡터를 구하는 방법은 동일하다. 아래와 같이 v → \overrightarrow{v} v
v → = [ 2 4 ] = 2 × i ^ + 4 × j ^ T r a n s f o r m e d v → = 2 × T r a n s f o r m e d i ^ + 4 × T r a n s f o r m e d j ^ \overrightarrow{v} = \begin{bmatrix} 2 \\ 4 \end{bmatrix} = 2\times\hat{i} + 4 \times \hat{j} \\ Transformed \quad \overrightarrow{v} = 2 \times Transformed\;\hat{i} + 4 \times Transformed \; \hat{j} v = [ 2 4 ] = 2 × i ^ + 4 × j ^ T r a n s f o r m e d v = 2 × T r a n s f o r m e d i ^ + 4 × T r a n s f o r m e d j ^
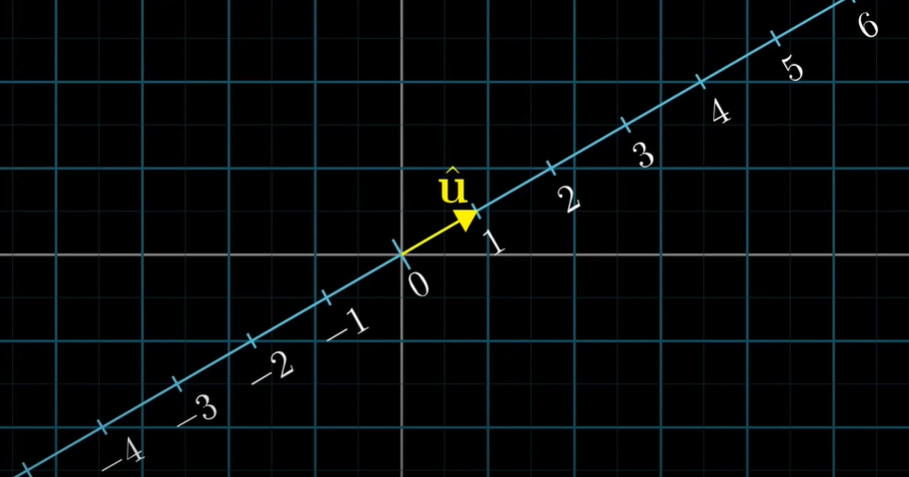
이를 조금 더 정확히 봐보자. 2차원 공간 안에 원점을 지나는 수선을 그린다.(원점이 겹치게) 그리고 그 수선을 따라 길이가 1인 u ^ \hat{u} u ^ 여기서 중요한 것은 u ^ \hat{u} u ^ u ^ \hat{u} u ^
만약, 위의 2차원 공간을 수선과 같아지게 차원을 축소한다면 어떻게 될까?i ^ \hat{i} i ^ u ^ \hat{u} u ^ i ^ \hat{i} i ^ u ^ \hat{u} u ^ i ^ \hat{i} i ^ u ^ \hat{u} u ^ u ^ \hat{u} u ^ i ^ \hat{i} i ^ i ^ \hat{i} i ^ u ^ \hat{u} u ^ x x x
j ^ \hat{j} j ^ u ^ \hat{u} u ^ j ^ \hat{j} j ^ u ^ \hat{u} u ^ y y y
A ( [ 1 0 0 1 ] ) = [ u ^ x u ^ y ] A(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}) = \begin{bmatrix} \hat{u}_{x} & \hat{u}_{y} \end{bmatrix} A ( [ 1 0 0 1 ] ) = [ u ^ x u ^ y ] 자, 그럼 위와 같은 선형변환을 거치는 공간 안에 또 하나의 벡터 w → \overrightarrow{w} w
w → = [ 2 3 ] T r a n s f o r m e d w → = [ u ^ x u ^ y ] × [ 2 3 ] = [ 2 × u ^ x 3 × u ^ y ] \overrightarrow{w} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \\ Transformed \; \overrightarrow{w} = \begin{bmatrix} \hat{u}_x & \hat{u}_y \end{bmatrix} \times \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \times \hat{u}_x \\ 3 \times \hat{u}_y \end{bmatrix} w = [ 2 3 ] T r a n s f o r m e d w = [ u ^ x u ^ y ] × [ 2 3 ] = [ 2 × u ^ x 3 × u ^ y ] 결국은 u ^ \hat{u} u ^ w → \overrightarrow{w} w 따라서 기하학적인 방법으로 2차원을 1차원으로 선형변환한 결과를 봐도 수식으로 접근한 결과와 동일하다는 것을 알 수 있다.
우리는 이렇게 생각해볼 수도 있다.
두 벡터를 내적하는 것은, 하나의 벡터를 선형변환의 결과로 봐도 된다
이중성(duality)
수학에는 이중성이라는 개념이 있고, 우리가 위에서 본 접근도 이중성을 사용한 것이다. 이중성이란 "어떤 공간을 수선으로 차원을 축소하는 선형변환을 할 때, 그 공간은 특정 벡터와 연관이 있다는 것"이다.
위에서 든 예시를 가져오자면, 2차원 공간을 u ^ \hat{u} u ^ u ^ \hat{u} u ^
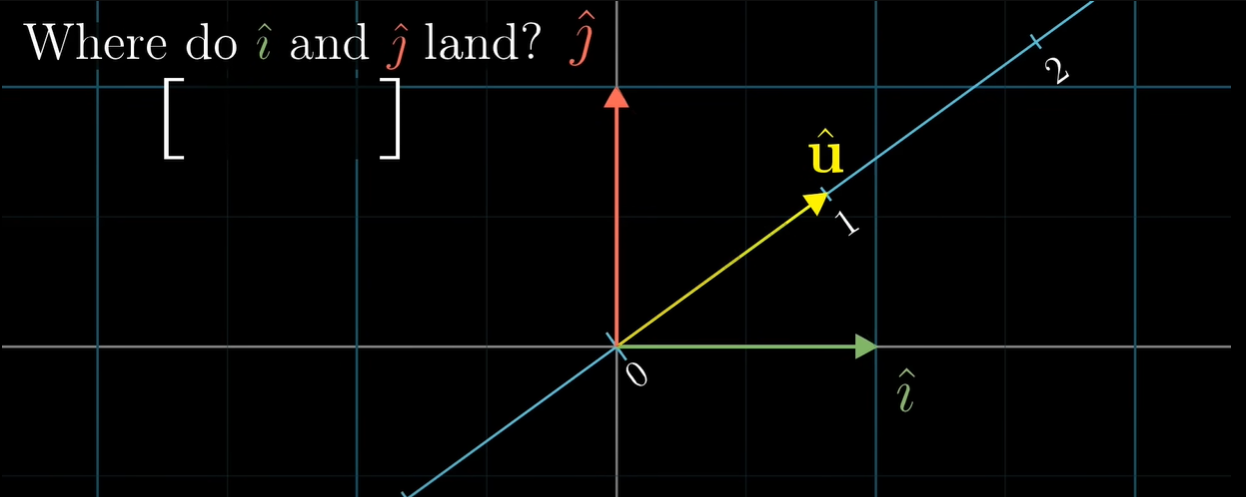먼저 를 에 투영한다고 생각해보자.
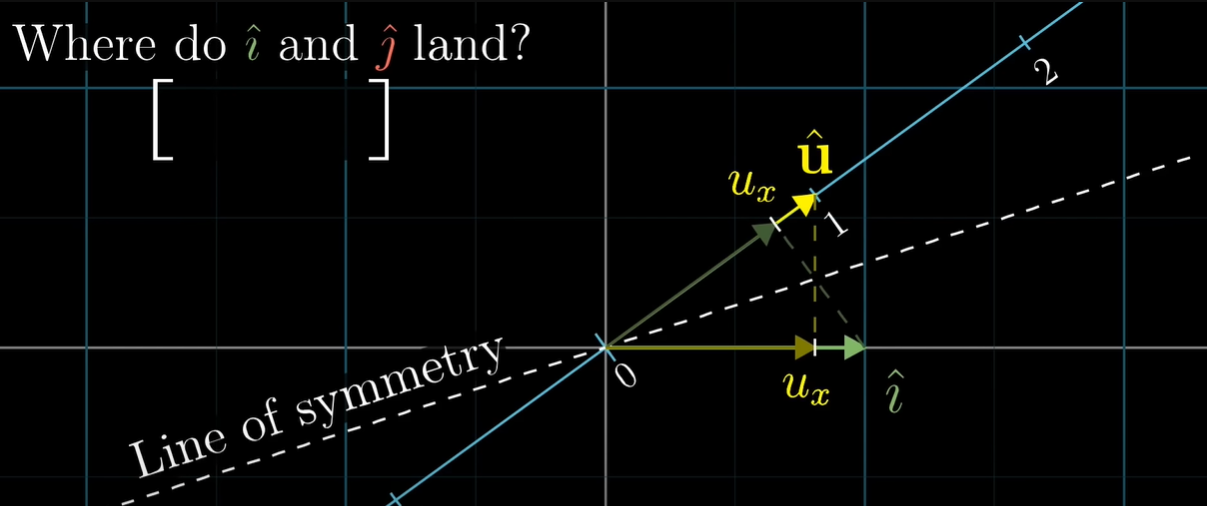과 는 길이가 같기 때문에 을 에 투영하나, 를 에 투영하나 그 길이는 같을 것이다. 따라서 선형변환 후의 위치는 의 좌표와 동일하다.