Essence of linear algebra - Chapter 3. Linear transformations and matrix

jwKim·2023년 1월 29일

❗ Essence of linear algebra

목록 보기

3/14

※ 선형 변환을 시각적으로 보는 것이 이해하기에 더 좋았다. 따라서 강의를 보면서 살펴볼것(벨로그에는 이미지밖에 넣지 못하므로 단편적이라 선형 변환을 이해하기에 한계가 있음) → 강의 주소
※ 선형 변환을 ppt로 나타내는 것은 한계가 있어 강의 화면을 캡쳐하겠다.

선형 변환은 무엇일까? 선형 변환을 알기 위해서 두 단어씩 끊어서 보자.

변환(transformation)
- transformation은 함수를 의미한다. 함수는 input을 받아 output으로 바꾸는데, 이와 같이 선형 변환은 input 벡터를 output 벡터로 바꾸는 것이다.
- 새로운 벡터가 짠!하고 나타나는게 아니라 공간을 변형시켜서 그 공간 안에 있는 벡터도 바뀌는 것임!(아래 그림처럼)
선형
- 모든 선들이 변환 후에도 직선이다.
- 원점은 변하지 않고 그대로 있다.
- 격자 무늬가 서로 평행하고(사다리꼴이 되더라도) 각 격자 무늬는 서로 동일한 간격으로 있어야한다.
  - => 선형 변환 후에도 벡터들 역시 격자선에 평행하고 균등하게 변화한다.

종합해보면, 선형 변환이란 직선의 형태와 원점을 유지하면서 어떤 공간에 변형을 주는 것이다.

선형 변환을 수치적으로 계산하려면 기저벡터( $\hat{i}, \hat{j}$ )가 어떻게 변하는지 알면 된다. 왜냐하면 어떤 공간 안에 있는 벡터들은 기저벡터로 전부 표현이 가능하기 때문에 선형 변환과 상관 없이 기저벡터를 사용해 구할 수 있기 때문이다.

예를 들어 아래 그림과 같은 벡터들이 있다고 하자. ( $\overrightarrow{v}$ 는 기저 벡터를 알면 구할 수 있다는 것을 보이기 위해 수식으로 표현)

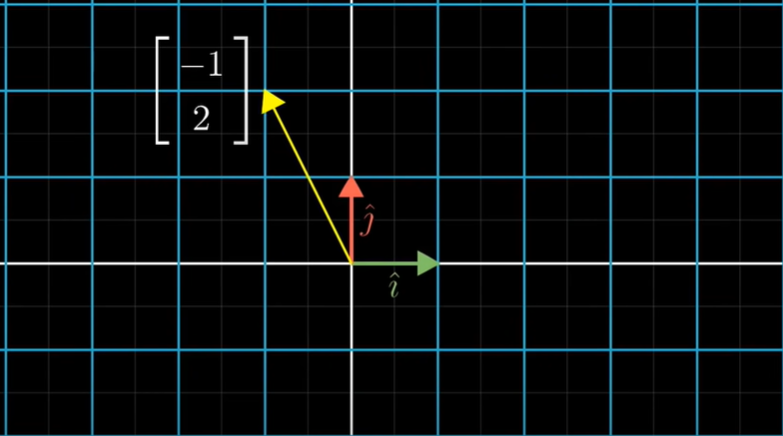\hat{i} = \begin{bmatrix} 1\\0 \end{bmatrix} , \quad \hat{j} = \begin{bmatrix} 0\\1 \end{bmatrix} ,\quad \overrightarrow{v} = -1 \times \hat{i} + 2 \times \hat{j}

이 2차원 공간을 선형 임의로 선형 변환하면 아래와 같다.

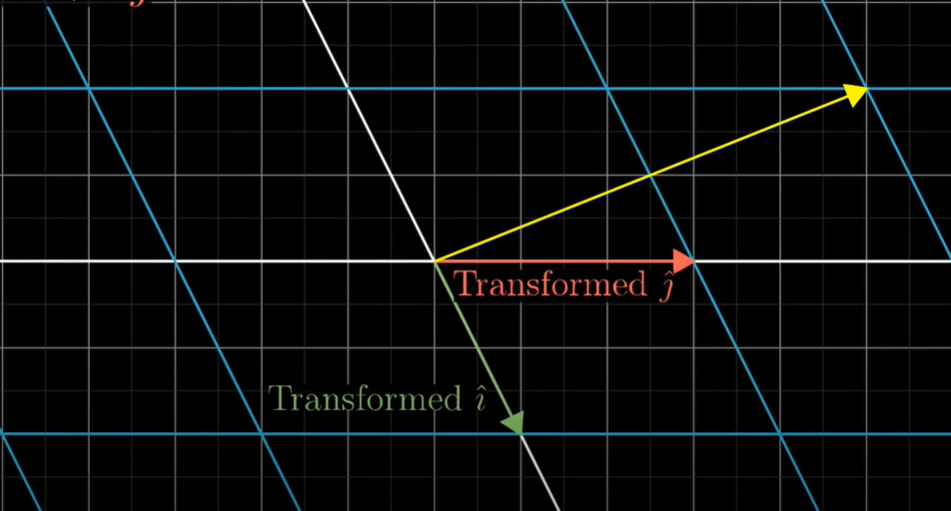기존 좌표 평면의 벡터들이 공간이 변화함에 따라 균등하게 변화했다. 앞서 살펴본 '선형'의 정의 대로 직선을 유지하고, 격자 선들과 평행하며 공간이 변화함에 따라 균등하게 길이가 변화했다.

바뀐 기저벡터들의 좌표는 아래와 같다.

Transformed\; \hat{i} = \begin{bmatrix} 1\\ -2 \end{bmatrix} ,\quad Transformed\; \hat{j} = \begin{bmatrix} 3\\ 0 \end{bmatrix}

그렇다면 바뀐 $\overrightarrow{v}$ 는 어떻게 될까?

Transformed\; \overrightarrow{v} = -1 \times Transdformed \;\hat{i} + 2 \times Transformed \; \hat{j} \\ = -1 \times\begin{bmatrix} 1\\-2 \end{bmatrix} + 2 \times \begin{bmatrix} 3\\0 \end{bmatrix} = \begin{bmatrix} 5\\2 \end{bmatrix}

선형 변환과 상관없이 $\overrightarrow{v}$ 는 $\hat{i}$ 에 -1배, $\hat{j}$ 에 2배를 해준다. 왜냐하면 선형 변환 후에도 $\overrightarrow{v}$ 는 여전히 선형 결합을 유지하기 때문이다.

따라서 선형 변환을 바뀐 벡터를 알기 위해서 변화환 기저벡터만 알면 된다.

그렇다면 선형 변환의 결과를 위와 같이 $\hat{i}$ , $\hat{j}$ 따로 써줘야 할까? 선형변환을 한 번에 나타내기 위해 우리는 행렬을 쓴다.

Transformed\;\hat{i} = \begin{bmatrix} 1\\-2 \end{bmatrix} , \quad Transformed\;\hat{j} = \begin{bmatrix} 3\\0 \end{bmatrix}

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$ ↓↓↓

A = \begin{bmatrix} 1 & 3 \\ -2 & 0 \end{bmatrix}

행렬이 의미하는 것은 선형 변환으로 바뀐 기저벡터를 나타낸 것이다. 첫 번째 축에는 $Transformed\;\hat{i}$ 를, 두 번쨰 축에는 $Transformed\;\hat{j}$ 를 써준다.

행렬의 의미를 가지고 선형 변환한 벡터를 표현 및 계산할 수 있다.

Transformed\; \overrightarrow{v} = A \overrightarrow{v} = \begin{bmatrix} 1 & 3\\ -2 & 0 \end{bmatrix} \begin{bmatrix} -1\\2 \end{bmatrix} = -1 \begin{bmatrix} 1\\-2 \end{bmatrix} + 2 \begin{bmatrix} 3\\0 \end{bmatrix} \\= \begin{bmatrix} -1 \times1 + 2\times3\\ -1\times(-2) + 2\times0 \end{bmatrix} = \begin{bmatrix} 5\\2 \end{bmatrix}

우리가 알고 있던 행렬과 벡터의 곱이 되었다! 사실 우리가 하나의 공식처럼 외우던 행렬과 벡터는 "원본 벡터 v를 선형 변환하면 어떻게 될까? "를 뜻하는 것이었다.

선형 변환은 공간을 이동하거나 회전 시키는 일을 의미한다. 선형 변환의 결과 공간이 변형되고 그에 따라 그 공간 안에 있는 모든 벡터들이 동일하게 변화한다.

기저벡터는 그 공간 안에 있는 모든 벡터들을 표현하는 기본 단위가 되므로, 선형 변환 후에도 기저벡터를 알면 변형된 공간의 모든 벡터를 표현할 수 있다.

행렬은 공간의 변화를 나타낸다. 행렬은 선형 변환으로 바뀐 기저벡터들을 하나로 합친것이다.(행렬과 벡터의 곱을 각각의 기저벡터로 나눠보면 왜 그렇게 연산되는지 알 수 있음)