Essence of linear algebra - Chapter 5. Three dimensional linear transformation

jwKim·2023년 2월 4일

❗ Essence of linear algebra

목록 보기

5/14

차원이 높아져도 선형변환에 대한 기본 개념은 바뀌지 않는다.

선형변환은 함수처럼 하나의 벡터를 입력 받아 하나의 벡터를 뱉어낸다.

선형변환을 진행해도 모든 직선들은 서로 평행하며 공간 전체가 변형되며 각 격자무늬는 일정한 비율을 유지한다.

원점은 그대로 원점으로 존재한다.

중요한 것은 지금껏 2차원에서 input 벡터를 "움직여서" output 벡터로 변경한 것처럼 3차원 이상의 공간에서 선형변환을 해도 동일하게 벡터를 움직여 변경한다. 여기서 움직인다는 뜻은 기저벡터가 변경됨에 따라 벡터가 바뀐다는 것이다.

3차원에서는 아래와 같은 기저벡터를 정의한다.

\hat{i} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \hat{j} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \hat{k} = \begin{bmatrix} 0 \\ 0\\ 1 \end{bmatrix}

그리고 y축을 기준으로 90도 회전한 결과는 다음과 같다.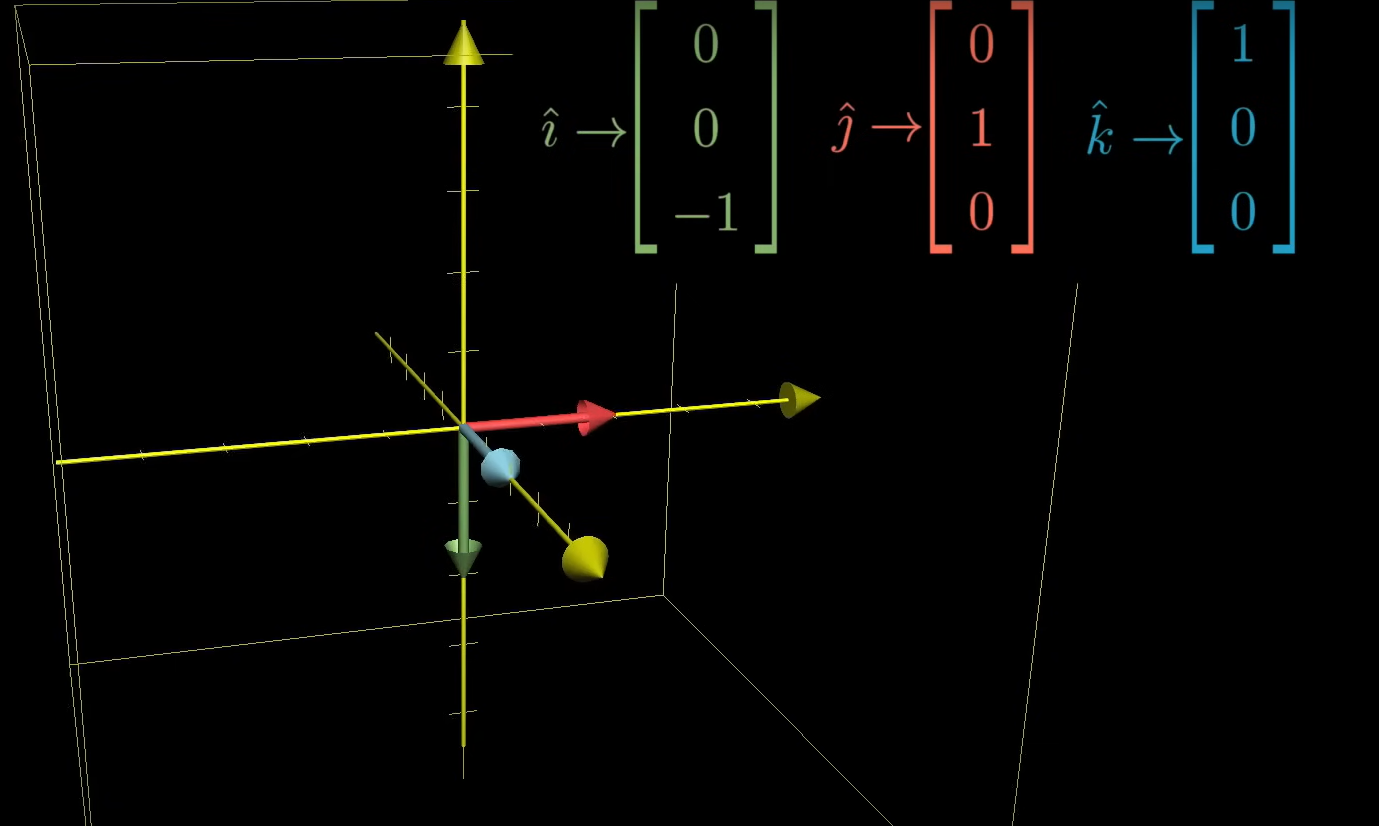 2차원에서처럼 바뀐 기저벡터가 좌표처럼 표현이 된다.

예를 들어 3차원 공간에 $\overrightarrow{v}$ 는 아래와 같이 기저벡터들의 조합으로 표현되고, 선형변환을 하면(기저벡터들의 집합인 행렬을 곱하면) 아래와 같이 식이 변하게 된다.

\overrightarrow{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} = x\hat{i} + y\hat{j} + z\hat{k}= \\ \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ -1 & 0 & 0 \end{bmatrix} \overrightarrow{v} = x\begin{bmatrix} 0 \\ 0 \\ -1 \end{bmatrix} + y\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + z\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}

선형변환은 차원에 관계없이 동일하게 작동한다.