행렬식(determinant)

선형변환은 모든 공간을 변형시키는 것이기에 그 안에 있는 모든 것들이 동일한 비율로 축소 혹은 확대된다. 그렇다면 선형변환을 할 때 공간을 얼마나 변형시키는지를 측정할 수 있지 않을까?

공간의 변환 정도를 측정하는 것이 바로 행렬식이다.

행렬식 : 선형변환을 할 때 단위 정사각형을 기준으로 공간이 얼마나 확대되는지, 혹은 얼마나 축소되는지 나타내는 값

$\begin{bmatrix} 3 & 0 \\ 0 & 2 \end{bmatrix}$ 변환을 하는 예를 살펴보자.
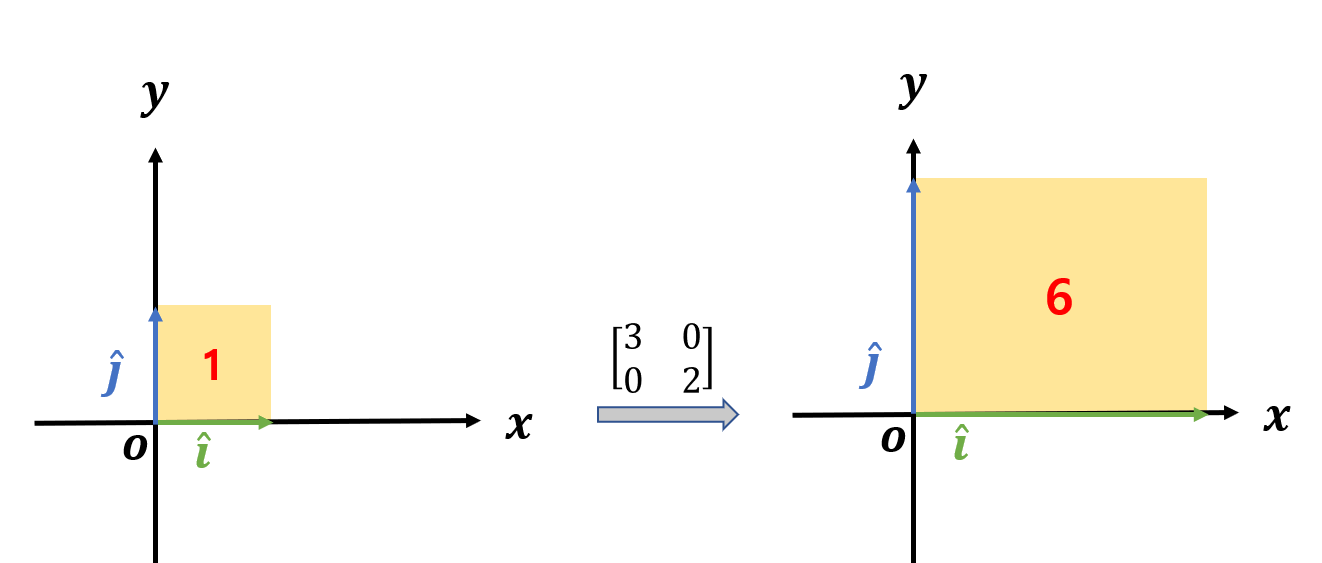기존의 기저벡터로 만들어지는 사각형의 넓이는 1이며 단위 정사각형이라고 하자. 선형변환의 결과로 사각형의 넓이는 6으로 바뀌었다. 선형변환의 결과는 모든 공간을 동일한 비율로 확대/축소 하므로, 이 사각형의 넓이가 6배 확대되었으면 다른 공간도 6배 확대되었다고 말해도 된다.

선형대수는 위 예시를 아래와 같은 용어로 표현한다.

• 선형대수에서는 이를 6팩터(factor) 만큼 확대했다고 말한다.
• 행렬식을 계산한다는 의미로 $det(\begin{bmatrix} 3 & 0 \\ 0 & 2 \end{bmatrix})=6$와 같이 표현한다.
• 6을 행렬식(determinant)라고 부른다.

행렬식은 공간이 변형되는 비율을 나타낸다. 따라서 행렬식이 0이면 모든 공간이 선이나 점으로 바뀐다. 어느 영역이던 공간의 크기가 0이 되는 것이다.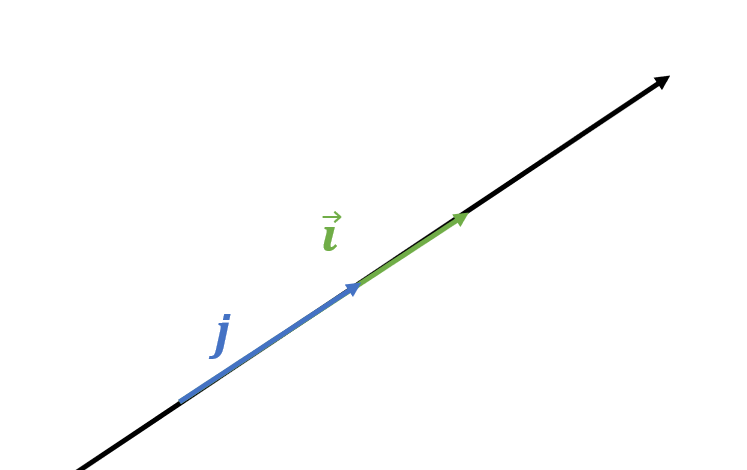(하나의 선이나 점 위에 두 개의 기저벡터가 놓이면 공간을 만들 수 없으므로 행렬식 0)

행렬식이 음수일 때

행렬식이 음수라면, 공간이 뒤집힌다는 의미를 같는다. 마치 A4 용지를 뒤집는 것과 같이 공간도 뒤집힐 수 있다.

기저벡터로 설명하면 아래와 같다.
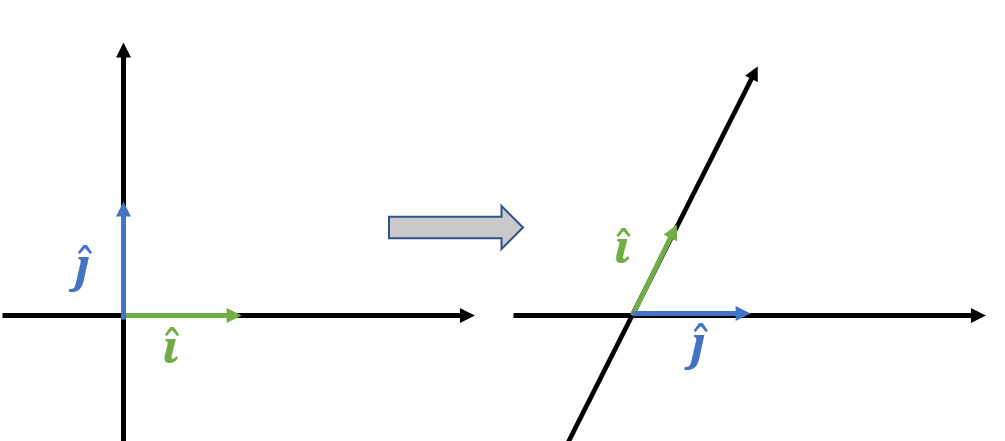원래 공간에서는 $\hat{j}$가 $\hat{i}$ 왼쪽에 있는데, 선형변환을 하면 $\hat{j}$가 $\hat{i}$ 오른쪽에 있다. 행렬식이 음수라면 이렇게 공간이 뒤집힌다! 그리고 행렬식의 절대값은 여전히 팩터이다.

< 행렬식이 음수이 음수인 경우 >

• det = -2 ⇒ 공간을 뒤집고, 2팩터만큼 공간을 확대하기
• det = -0.2 ⇒ 공간을 뒤집고, 0.2만큼 공간을 축소하기

3차원에서의 행렬식

3차원에서도 행렬식은 공간을 스케일링하는 비율을 알려주지만, 3차원 공간에서의 행렬식은 부피를 나타낸다.(2차원은 면적, 3차원은 부피)

부피가 $1\times1\times1$인 단위 정육면체를 그리고 선형변환 후의 평행육면체(parallelepiped)의 부피를 구하여 행렬식을 구한다.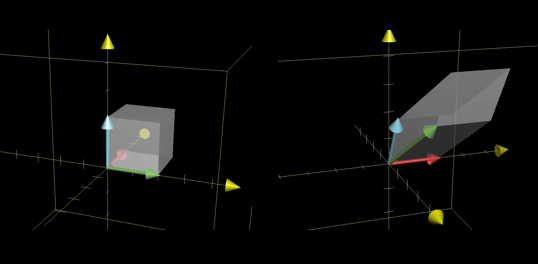

3차원에서 행렬식이 음수라면 어떨까? 3차원 공간에서 공간을 뒤집는다는 것은 쉽게 상상이 되지 않는다. 이 때 우리는 '오른손 규칙'을 사용할 수 있다.
엄지는 $\hat{k}$를, 검지는 $\hat{i}$를, 중지는 $\hat{j}$를 의미하는데, 선형변환 후에도 오른손으로 그 공간을 표현할 수 있다면 행렬식은 양수이고, 선형변환 후에는 왼손으로 표현할 수 있다면 행렬식은 음수이다.

행렬식의 계산

행렬식을 계산하는 공식은 아래와 같다.

만약 $b$와 $c$가 0이라면, 맨 위에서 들었던 2차원 선형 변환과 같이 단위 정사각형이 직사각형 형태로 나오며 행렬식은 $ad$로 계산된다.

만약 $b$나 $c$ 둘 중 하나가 0이라면 어떻게 될까?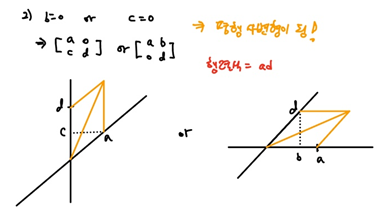위와 같이 공간이 찌그러져 평행사변형 형태로 나오며 행렬식은 $ad$로 계산된다.

Quiz

아래에 있는 식은 참이다. 왜 그럴까?

우선 숫자를 넣어 계산해 보았다.

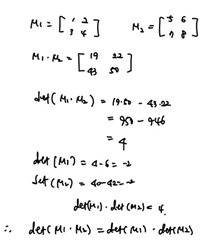
다음으로는 일반화가 되는지 확인하기 위해 문자를 넣어 식을 계산해 보았다.

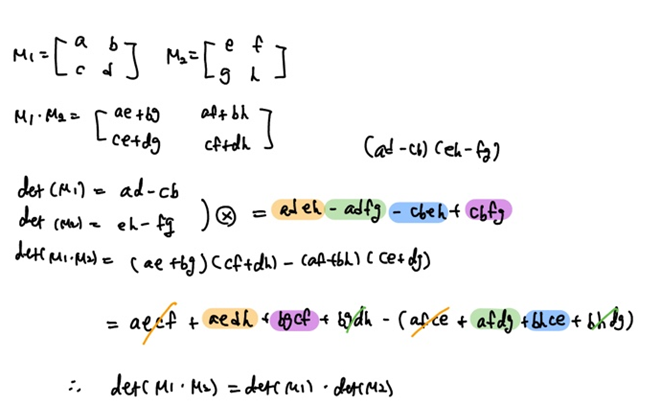
수식으로 계산하면 두 결과가 같다. 그런데 직관적으로 생각해보면, 두 선형변환을 동시에 하거나, 각각 따로 하거나 결과가 동일하기 때문이다.(4강 내용 참고)

따라서 직관적으로 생각해보나 수식으로 확인해보나 두 행렬식은 같다.