연립방정식

선형대수는 어떤 연립 방정식이던 표현 및 해결이 가능하다고 한다. 아래와 같은 연립방정식이 있다.

해당 연립방정식은 계수, 미지수, 상수항끼리 각자 모아서 표현할 수 있다.

이렇게 연립방정식은 행렬과 벡터로 나눌 수 있는데, 기호로 표기하면 아래와 같다.

그리고 이를 해석하면, "선형변환하여 $\overrightarrow{v}$가 되는 $\overrightarrow{x}$가 있는지 찾는 일"이다.

연립방정식의 해와 역행렬

연립방정식의 해는 선형변환의 결과로 차원이 낮아지는지를 확인해야한다.(=행렬식이 0이 되는지 아닌지)

1) 행렬식 $\ne 0$
$\overrightarrow{x}$와 $\overrightarrow{v}$이 1대1 대응이고 해가 1개이다. 이는 선형변환을 선형변환을 역으로 하면 $\overrightarrow{v}$를 통해 $\overrightarrow{x}$를 찾을 수 있다는 뜻이다.

여기서 역행렬의 개념이 나온다. 역행렬은 선형변환한 결과를 선형변환하기 전으로 돌리는 행렬을 의미하며 $A^{-1}$로 표기한다.

따라서 $det(A) \ne 0$이라면, $A$의 역행렬 $A^{-1}$은 존재한다.

※ $A • A^{-1}$은 단위행렬(identity matrix)가 나온다.

단위행렬은 대각선에 위치한 원소들만 1이고 다른 원소들은 전부 0인 행렬이다. 크기는 정사각형이다.

$I_{n}= \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & 0 & \cdots & 1 \end{bmatrix} \in \mathbb{R}^{n\times n}$

2) 행렬식 = 0
행렬식이 0이어도 해는 존재할 수 있다. 공간이 선이나 점이 될 때 $\overrightarrow{v}$가 그 선 위에 있는 경우에는 해를 구할 수 있다.

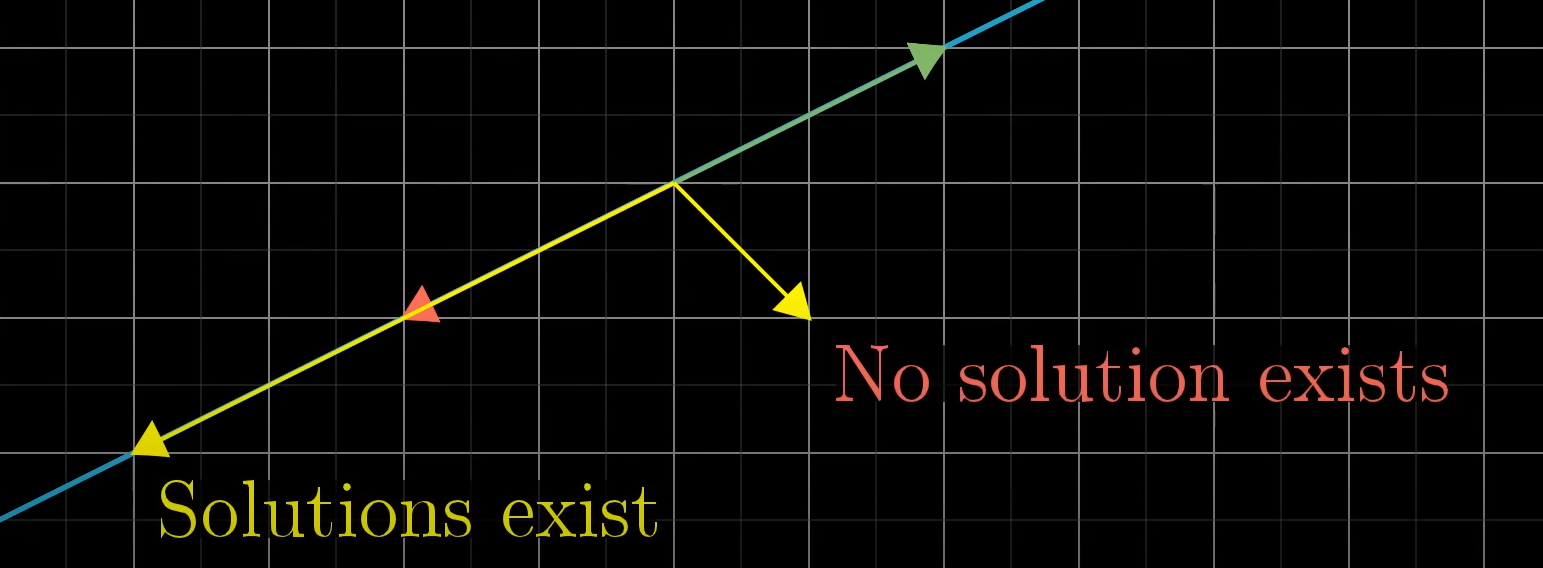
그런데 선형변환한 결과로 원본 벡터로 다시 변환할 수 없다. 따라서 역생렬이 존재하지 않는다. 공간을 축소해 선으로 만드는건 가능한데 왜 선을 늘려 공간으로 바꾸는 것은 불가능할까?

하나의 선을 공간으로 넓히면 원본 벡터를 추청해서 여러 개 그려야한다.(다대1 대응) 그런데 선형변환은 하나의 함수이기 때문에 input과 output이 한개씩 대응되어야 한다. 따라서 선을 공간으로 펼칠 수 는 없다.

Rank와 열공간(Column space)

Rank는 선형변환의 결과가 몇차원인지 나타낸다. Rank 1은 선형변환의 결과가 1차원원(=선)인 경우이고, Rank 2는 선형변환의 결과가 2차원(=평면)인 경우를 뜻한다. 선형변환의 결과로 차원의 수가 변하지 않는 경우에 Full Rank라고 한다.

선형변환의 결과가 선이건, 면이건, 부피이건 간에 행렬을 통해 가질 수 있는 결과 집합을 열공간(Column space)라고 한다. 행렬은 기저벡터를 열로 구분하여 나열한 것이기 때문에 행렬은 선형변환의 결과공간을 의미한다.

두 개념을 결합해보면, Rank는 선형변환의 결과 집합인 열공간의 차원수를 의미한다.

[ span과 column space의 차이? ]

• 기저벡터로 만들 수 있는 모든 벡터의 집합
• 열 공간은 기저벡터를 모아놓은 그 자체이다. 따라서 행렬 그 자체를 의미한다.

영공간(Null space)

$\begin{bmatrix}0 \\0 \end{bmatrix}$은 어떤 행렬이던 포함되어있다. 선형대수에서는 모든 벡터를 원점에서 시작하기 때문이다.

$A\overrightarrow{x} = \begin{bmatrix}0 \\0 \end{bmatrix}$이라면, 그 방정식의 해는 무수히 많다.

만약 아래 그림과 같이 1사분면과 3사분면을 가로지르는 벡터가 있는데, 선형변환을 하나의 선으로 공간을 축소한다면 모든 벡터가 원점에 모이게 된다.

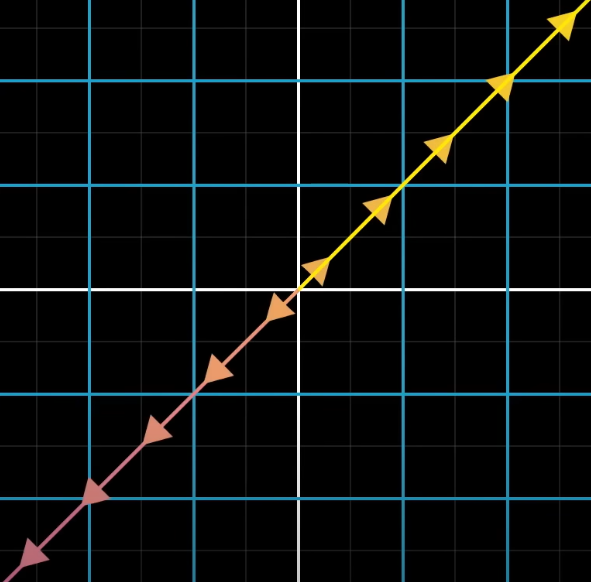
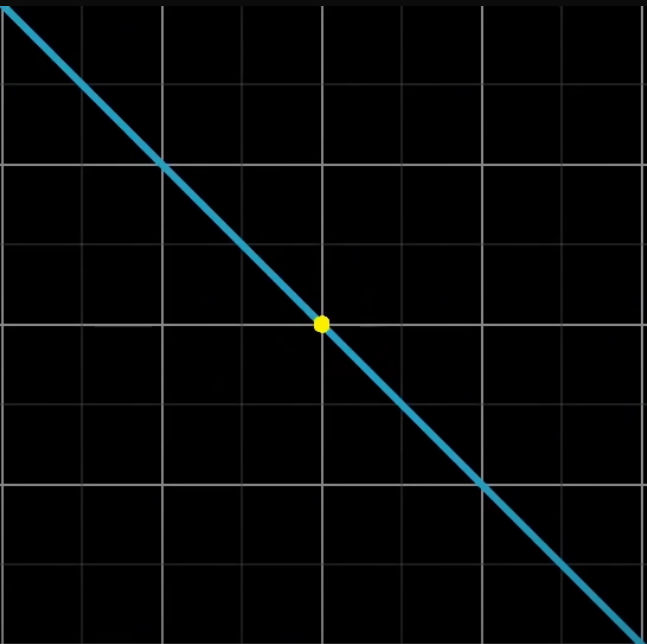
선형변환 후 결과가 원점이 되는 벡터들의 집합을 영공간(null space)라고 하거나 커널(kernel)이라고 한다.