직사각형 행렬

지금까지는 아래와 같은 정사각형 행렬만을 다루었다.

그런데 선형대수에서는 직사각형 행렬도 있다.

이런 행렬들은 무엇을 의미할까?

1) 세로로 긴 행렬

행렬에서 행의 개수는 해당 공간의 차원 수를 나타내고, 열의 개수는 기저벡터의 개수를 의미한다.

$\hat{i} = \begin{bmatrix} 2 \\ -1 \\ -2 \end{bmatrix}, \hat{j} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}$로 나눌 수 있고 각 기저벡터는 3개의 좌표값을 가지므로 3차원이다.

위 행렬에서 기저벡터는 2개이므로(열이 2개) 공간에 그려보면, 기저벡터가 2개이므로 평면이 만들어진다. 그리고 높이를 지정하는 $\hat{k}$가 존재하지 않으므로 원점을 지나는 평면이 된다.(그림 자료를 넣기 애매해서 pass)

따라서 위 그림은 2차원에서의 평면을 그대로 3차원으로 가져갔다고 생각하면 된다.



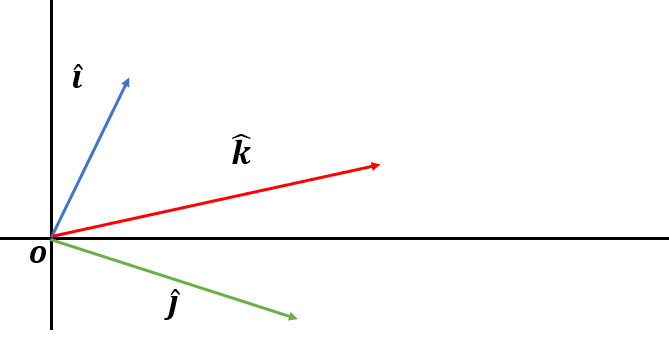
2) 가로로 긴 행렬

위 행렬은 2차원 공간에 기저벡터가 3개 존재한다는 의미이다.