[Deep Learning] Perceptron 알고리즘 박살내기(+code)

Steven Lee·2023년 9월 3일

AI Deep Learning

TRINITY

목록 보기

1/3

퍼셉트론(Perceptron) 이란?

간단한 이진 분류기(binary classifier)를 만들기 위한 기본적인 인공 신경망 모델.

1957년 미국의 프랑크 로젠블라트가 개발했으며, 입력값을 받아 각 입력에 대한 가중치를 곱하고, 이를 모두 더한 후에 활성화 함수를 통과시켜 최종 출력을 생성하는 구조를 지닌다.

📌이진 분류기(Binary Classifier)

주어진 요소들을 두 개의 그룹(class)로 "분류" 시키는 것 - 각 요소의 특성(feature)들을 토대로 분류
ex) 비가 온 날 (특성 - 하늘이 어두움, 무릎이 시큰함) / 비가 오지 않은 날 (특성 - 하늘이 밝음, 무릎이 시큰하지 않음)

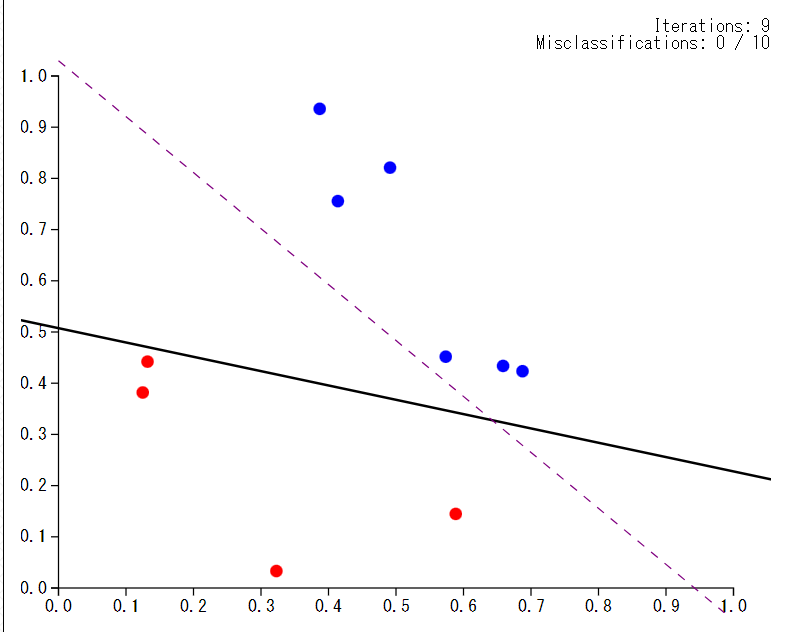
사진처럼 빨간 점인지, 파란 점인지를 나누는 것이다. 검은색 직선을 기준으로 두 점(클래스)이 "분류"된 것을 알 수 있다.

📌 인공 신경망(Artificial Neural Network)

인간의 두뇌로부터 영감을 받은 알고리즘으로, 생물학적 뉴런이 서로 간에 신호를 보내는 방식을 모방한 알고리즘

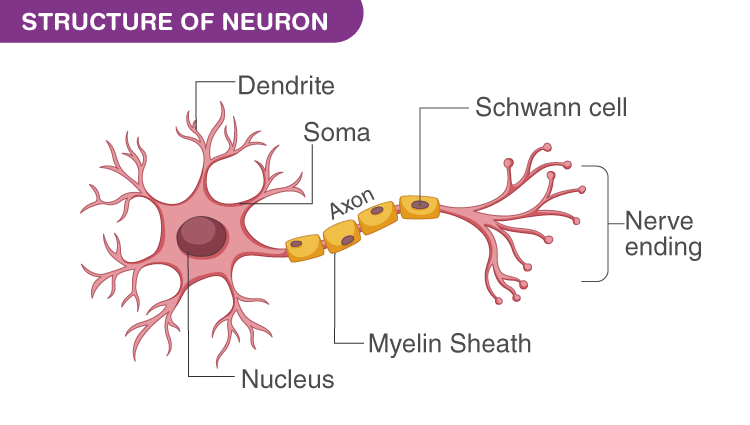
Dendrite(수상돌기) : 타 뉴런에게 전기 신호를 받는 곳

Synapse(시냅스) : 다른 뉴런과 수상 돌기의 연결 부위에 존재하며, 전기 신호의 세기를 재조정 하는 곳

Soma(세포체) : 여러 수상 돌기가 받은 전기신호를 모두 통합

Axon(축삭돌기) : 세포체의 전위가 일정 이상이 되면 이웃 뉴런에게 전기 신호 전송

위의 기능들을 이용해서 뉴런은 이웃 뉴런에게 전기 신호의 전송 유무를 조절함으로서 두뇌 활동의 기초적인 Base를 제공한다.

Logic

수상 돌기를 통해 이웃 뉴런에게 전기 신호를 받고, 그 신호의 세기를 재조정한다.

각 뉴런들이 연결된 세포체가 각 전기 신호를 모두 통합한다.

통합한 전위값이 임계값을 넘어서면, 축삭돌기를 통해 다른 뉴런을 향해 전기 신호가 전송된다.

1~3 과정을 각 뉴런이 반복한다.

퍼셉트론의 구조

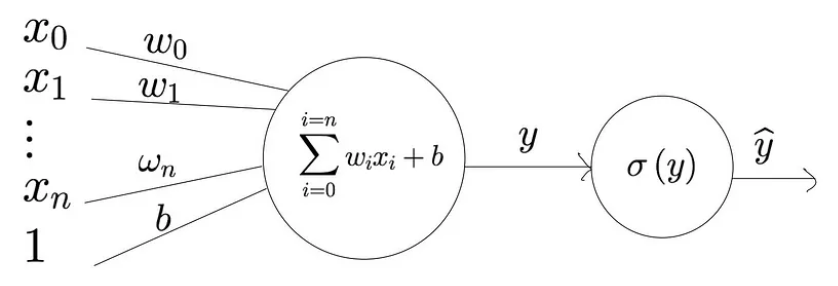
Structure of Perceptron

퍼셉트론의 정의에서 언급한 것을 참고로, 간단하게 구조를 나눠보자.

Inputs(입력) : 위 그림에서 x값은 입력의 특성값을 나타낸다. 예를 들면 하늘의 어둡기, 무릎이 시큰한 정도이다. 이 특성 값은 가중치(변수 w)값과 곱해지게 되는데, 여기서 가중치는 해당 특성이 차후 결과값에 얼마나 주요한 영향을 미치는지 결정해주는 값이다. 따라서 입력값은 아래와 같은 수식으로 나타낼 수 있다.
Summation & Activation : 입력된 특성 값들은 가중치 값과 곱해지고, 곱해진 각 값들은 아래와 같이 더해지게 된다.
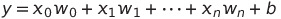
이처럼 더해진 값은 Activation function을 지나고 최종 output이 도출된다.
Activation function은 어떤 출력을 입력값으로 받아서 일종의 정규화를 수행하는 간단한 함수라고 보면 된다. 퍼셉트론에서는 선형 이진 분류를 수행할 것이기 때문에 여기서 사용할 활성화 함수는 아래의 Step function이다.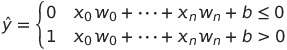
이와 같은 Activation function을 사용하게 되면 특정 결과값이 0 보다 큰지 작은지에 따라 두 개의 class로 분류를 할 수 있게 된다.

💡 b는 뭘까?

인공 신경망 알고리즘을 따른다면, output은 input의 총합을 특정 "임계값"과 비교해서 결정된다.(뉴런에서 세포체의 전위값이 일정 이상이 되어야 전기 신호를 이동시키는 것을 떠올려보자.) 따라서 임계 값을 theta라고 했을 때, 우리는 step function을 다음과 같이 작성할 수 있다.
식의 간소화를 위해 식 하나의 임계값 theta를 좌항으로 넘겨보자 b=-θ라고 한다면 다음의 식을 얻을 수 있고,
이 식은 우리가 class 분류를 할 때 사용한 Activation fn의 식과 일치함을 알 수 있다.
따라서 b값은 임계값의 역할을 하는 값이며 머신러닝 분야에서 이 값을 절편, 혹은 Bias라고 부른다.

퍼셉트론의 학습 규칙

가중치(weight)를 0 또는 랜덤한 작은 값으로 초기화
각 요소별로 y값을 계산
1) 계산 y값과 실제 y값을 비교하여 가중치 업데이트

퍼셉트론은 학습시킨 모델의 각 가중치 값을 토대로, 추후 들어오는 미지의 데이터가 어떤 클래스에 속하는지 판별함을 목적으로 하기 때문에 보다 정확한 판별을 위해 가중치의 조정은 무엇보다 중요하게 다뤄진다. 가중치의 조정은 Error의 최소화와 같은 의미이며, 따라서 Activation 단계 뒤에 위치하게 된다.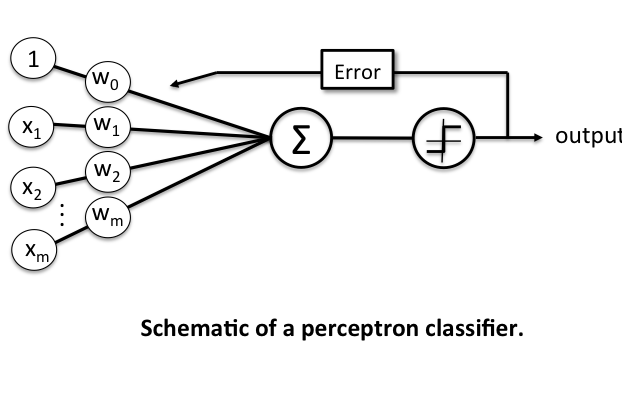

가중치 업데이트 수식

가중치 벡터 w에 있는 개별 가중치 w(j)가 동시에 업데이트 되는 것을 다음과 같이 쓸 수 있다.
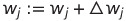그리고 가중치 w(j)를 업데이트하는 데 사용되는 델타 w 값은 퍼셉트론 학습 규칙에 따라 계산된다.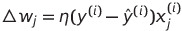
각각 간단히 설명을 해보자면,

n : 학습률(learning rate), 일반적으로 0에서 1사이의 값을 가진다
y(i) : i번째 훈련 샘플의 진짜 클래스 레이블
y^(i) : i번째 훈련 샘플의 예측 클래스 레이블

수식 자체가 굉장히 간단하고 효과적으로 작동함을 알 수가 있다. 퍼셉트론 모델 사용자는 y값이 임계값보다 크냐 작냐에 따라 클래스를 분류한다. 만약 실제 클래스는 1 (y>임계값)이지만 0 (y<임계값)으로 예측했다고 생각해보자.

x값이 양수라고 가정한다면, 델타 w의 값은 y-y^의 값이 1이므로 양수의 값을 가지게 될 것이다.
양수의 값이 더해질 것이므로 w의 값이 증가한다.
x는 그대로이고 w만 증가했으므로 x*w 값들의 총합인 y의 값 또한 증가하게 될 것이다.(위의 수식들을 하나하나 참고하자)
결국 y 값은 임계값보다 커질 가능성이 높아지게 되고, 올바르게 가중치 업데이트가 되었음을 알 수 있다.

위의 작업을 반복하게 된다면 궁극적으로 가장 적합한 가중치 값을 얻을 수 있을 것이다.

💡 해당 반복 작업을 시각적으로 볼 수 있는 사이트를 참조해보자. https://vinizinho.net/projects/perceptron-viz/

퍼셉트론 알고리즘 코드 구현

Perceptron Class

import numpy as np

# 퍼셉트론 구현
class Perceptron:
    def __init__(self, eta=0.01, n_iter=50, random_state=1):
        # eta: 학습률 (0.0 ~ 1.0 사이의 실수)
        self.eta = eta
        # n_iter: 학습 데이터셋 반복 횟수 
        self.n_iter = n_iter
        # random_state: 가중치 무작위 초기화를 위한 난수 생성기 시드
        self.random_state = random_state
    
    # 훈련 데이터 학습
    # X: 학습 데이터셋
    # y: 타깃 벡터
    def fit(self, X, y):
        rgen = np.random.RandomState(self.random_state)
        self.w_=rgen.normal(loc=0.0, scale=0.01, size=1+X.shape[1])
        self.errors_=[]

        for _ in range(self.n_iter):
            errors = 0
            for xi, target in zip(X,y):
                update=self.eta*(target-self.predict(xi))
                self.w_[1:]+=update*xi
                self.w_[0]+=update
                errors+=int(update!=0.0)
            self.errors_.append(errors)
        return self

    def net_input(self, X):
        return np.dot(X,self.w_[1:])+self.w_[0]
    
    def predict(self, X):
        return np.where(self.net_input(X)>=0.0, 1, -1)

데이터 가져오기(붓꽃 데이터)

import numpy as np
import pandas as pd

f = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", header=None)

y = df.iloc[0:100,4].values
y= np.where(y=='Iris-setosa',-1,1)

X = df.iloc[0:100,[0,2]].values

아래와 같은 데이터 Get

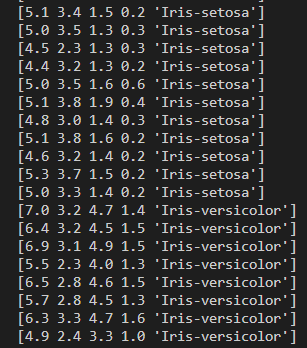
모델 학습 및 시각화

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X,y)

def plot_decision_regions(X,y,classifier,resolution=0.02):
    # 마커와 컬러맵을 설정합니다.
    markers=('s','x','o','^','v')
    colors=('red','blue','lightgreen','gray','cyan')
    cmap=ListedColormap(colors[:len(np.unique(y))])

    # 결정 경계를 그립니다.
    x1_min,x1_max=X[:,0].min()-1,X[:,0].max()+1
    x2_min,x2_max=X[:,1].min()-1,X[:,1].max()+1
    xx1,xx2=np.meshgrid(np.arange(x1_min,x1_max,resolution),np.arange(x2_min,x2_max,resolution))

    Z=classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z=Z.reshape(xx1.shape)

    plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())

    # 샘플의 산점도를 그립니다.
    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl,0],y=X[y==cl,1],alpha=0.8,c=colors[idx],marker=markers[idx],label=cl,edgecolor='black')

plot_decision_regions(X,y,classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()

결과 창

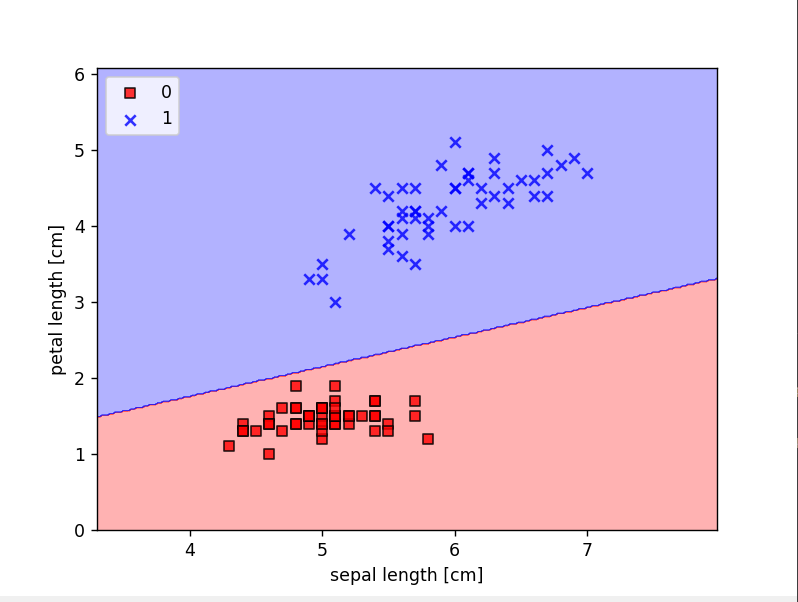
퍼셉트론의 한계

퍼셉트론은 경계를 나누는 경계면이 선형 결합의 형태를 띄기 때문에, 선형 분리 가능한 문제에 대해서만 학습이 가능하며, 즉, 하나의 초평면(hyperplane)으로 데이터를 분류할 수 있는 경우에만 적용이 가능하다. 즉, 오직 직선으로만 이루어진 경계면으로만 클래스를 분류할 수 있다는 의미이다.

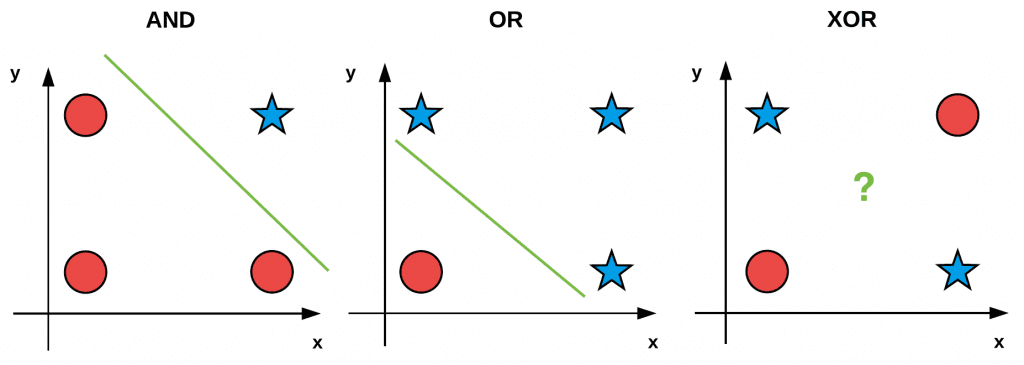
💡 Perceptron XOR Problem

1969년에 Marvin Minsky와 Seymour Paper가 “Perceptrons: an introduction to computational geometry”라는 책을 통해 퍼셉트론과 같은 Single Neural Network의 한계를 수학적으로 증명하며 인공 신경망 분야의 암흑기를 열었다.

뉴런이 하나인 경우에는 하나의 직선만을 그을 수 있다는 배경지식과 함께 위의 사진을 본다면 AND와 OR, NAND gate의 구현은 가능하지만, XOR gate는 절대로 하나의 직선으로 구현할 수 없다는 것을 알 수가 있다.

추후 이 문제는 다층 퍼셉트론과 역전파와 같은 개념의 등장으로 인해 해결되었다 -> 다음 포스팅에 관련 내용을 다룰 예정