[Deep Learning] Back-Propagation(역전파) 뿌셔보자 + Code

Steven Lee·2023년 9월 10일

TRINITY

목록 보기

2/3

Recap

지난 글에서 인공 신경망의 가장 기초적인 단계인 Perceptron에 대해 알아봤다. 짧게 복습해보자면 Perceptron은 이진 분류기로, 입력값에 곱하는 가중치 값을 조절하여, 두 개를 곱한 값이 일정 임계값 이상인지 이하인지에 따라 두 개의 클래스 중 어디에 속하는지 분류했다.

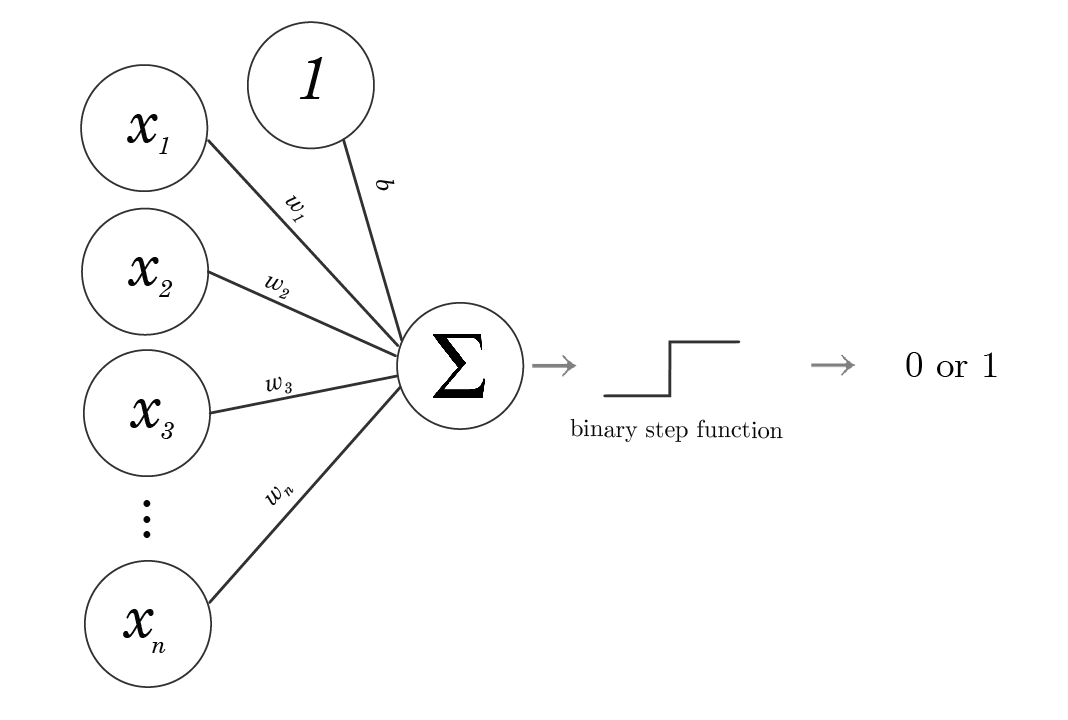
그러나 Perceptron은 두 클래스 밖에 분류를 못하고, 단일 선형 분류밖에 하지 못하기 때문에, 한계에 직면했다 (XOR 한계)

따라서 해당 문제를 해결하기 위해, 단일 선형 분류가 아닌 다중 선형 분류를 가능케 하는 다중 퍼셉트론 개념이 등장했고, 이에 따라 HIDDEN LAYER, 즉 은닉층의 개념 또한 등장하게 된다.

다층 퍼셉트론

다층 퍼셉트론은 말그대로 "여러 개의 퍼셉트론"으로 이루어진 퍼셉트론이다. 또한 다층 퍼셉트론은 단층 퍼셉트론과 다르게, 은닉층이라는 입력층과 출력층 사이에 하나의 층을 더 추가한다. 따라서 비선형적으로 분리되는 데이터 또한 학습이 가능케 하는 구조를 가질 수 있게 된다. 그리고 이러한 은닉층이 포함된 인공 신경망을 심층 신경망이라 부르며, 심층 신경망 학습을 위해 고안된 특별한 알고리즘을 우리는 딥러닝이라 부른다.

순전파(Feedforward)

다층 퍼셉트론에서는 입력 노드에서 나온 값들이 은닉층의 모든 노드들에게 전달되고, 또한 은닉층의 노드들에서 나온 값들은 모두 출력층의 모든 노드에게로 전달되게 된다. 앞에서 뒤로 자연스럽게 진행되는 이러한 계산 전달 방식을 순전파(feedforward) 라고 부른다.

우리는 순전파 방식의 전달 방식을 단층 퍼셉트론 알고리즘에서 봤기 때문에 어색하지 않게 받아들일 수 있다. 그러나 단층 퍼셉트론을 다층 퍼셉트론과 비교할 때 의문이 하나 생기는데, 그것은 가중치 값을 update할 때 이다.

단층 퍼셉트론에서는 출력층에서 Activation Function을 나온 결과 값(예측 값)이 실제 값과 어떤지를 비교한 뒤 가중치 값을 조절했었다. 물론 다층 퍼셉트론 또한 단층 퍼셉트론이 모여져서 만들어진 것이기 때문에 같은 방식을 적용하면 되지만, 문제는 은닉층으로 데이터 값이 전달될 때이다. 우리는 최종적인 출력층에서의 실제 값을 알고 있지, 은닉층에서 어떤 값이 나와야하는지는 알지 못한다. 즉, MNIST 문제에서 손글씨가 8라는 값을 예측해야한다는 것은 알지만, 그 전 단계(은닉층)에서는 어떤 값을 가져야하는지는 모른다는 것이다.

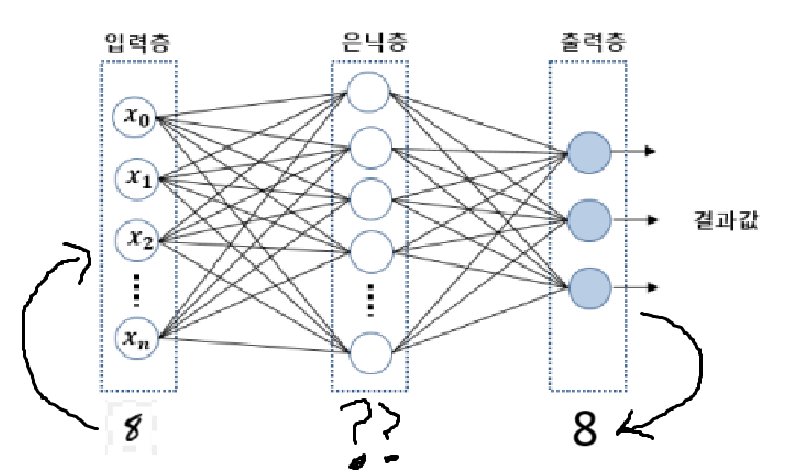
이에 따라 은닉층에서는 오차 값과 실제값 비교 계산을 할 수 없다는 말과 같고 오차 계산을 할 수 없으면? 가중치를 update할 수 없으며, 이는 최종적으로 학습을 할 수 없다는 말과 동일하다.

이러한 문제를 해결하고자, 다층 퍼셉트론을 말할 때 빠질 수 없는 개념인 역전파 개념이 등장하게 된 것이다.

역전파(Back-Propagation)

순전파라는 단어를 듣고 역전파를 듣는다면, 내용이 뭔지는 몰라도 순전파와 반대되는 "역"방향으로 진행될 것이라는건 예상할 수 있을 것이다.

역전파란 역방향으로 오차를 전파시키면서 각 층의 가중치를 업데이트 하는 알고리즘을 말한다. Optimizer로 경사하강법을 쓴다 가정했을 때, 비용함수를 업데이트 시키고자 하는 가중치로 미분하여 learning late를 곱하고, 기존의 가중치에서 빼서 가중치 값을 업데이트 시키면 역전파 알고리즘을 실행했다고 말할 수 있다. 그리고 수식은 다음과 같다.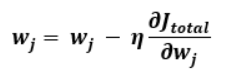

그리고 수식 마지막의 편미분 계산은 미적분학의 Chain Rule을 적용하면 다음과 같이 분해시킬 수 있다.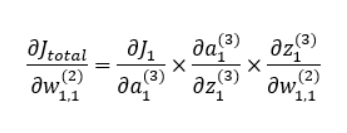

이처럼 분해를 하게 되면 충분히 계산이 가능한 형태를 띄게 되고, 이는 곧 가중치 업데이트가 충분히 가능하다는 말을 일컫는다.

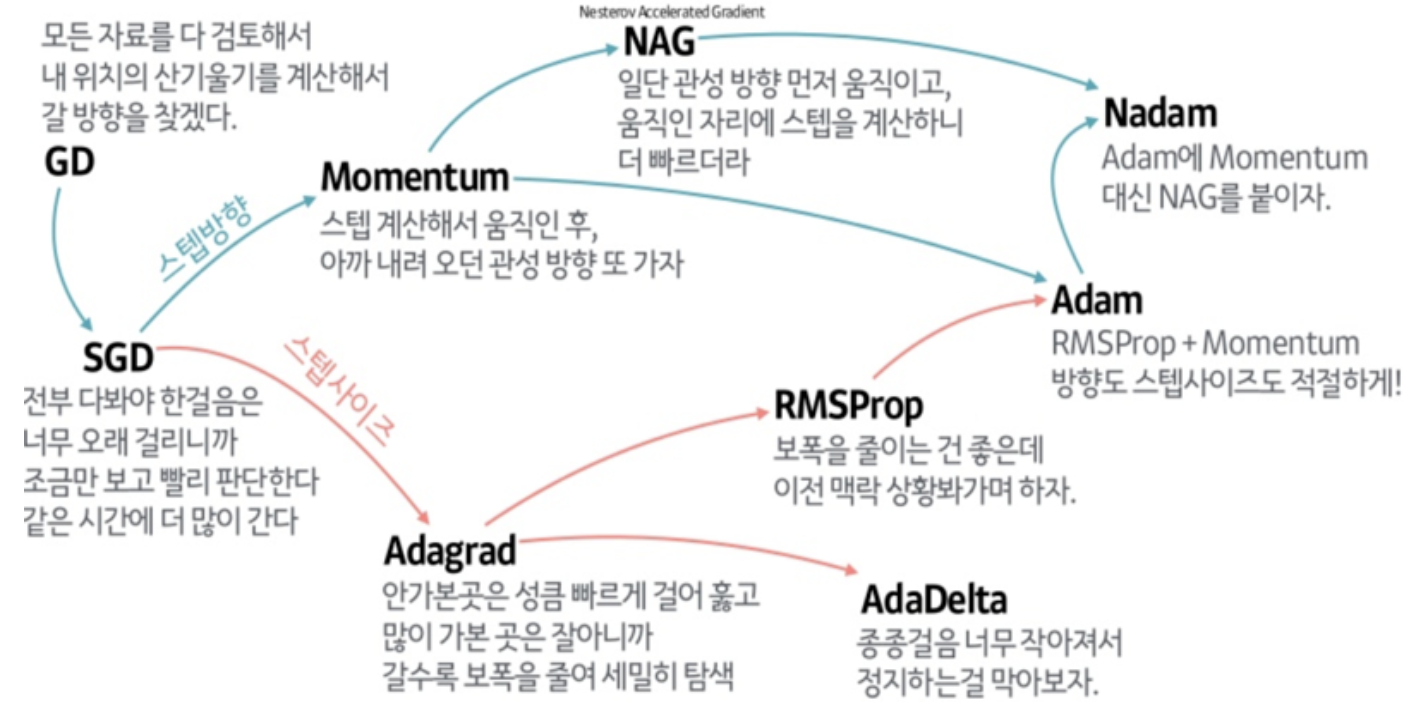
인공 신경망 학습 알고리즘에서 가장 중요한 것은 결국 실제 결과값과 예측 결과값의 오차를 최대한 줄이는 것이고, 이는 곧 Loss 함수(비용 함수)의 최솟값을 찾는 과정을 의미한다. 그리고 이러한 과정에 쓰이는 알고리즘을 Optimizer이라 부르며, 가장 유명하게 쓰이는 알고리즘 중 하나가 Gradient Descent(경사 하강법)이다.

https://github.com/Jaewan-Yun/optimizer-visualization
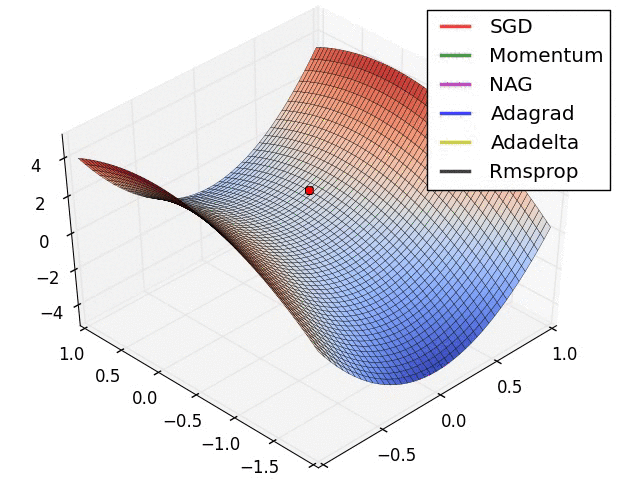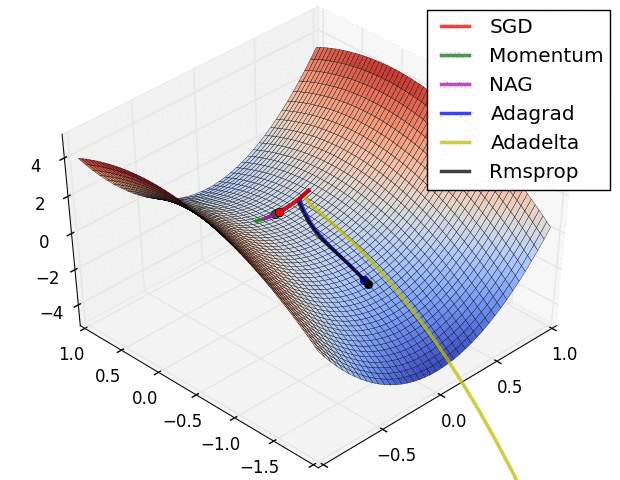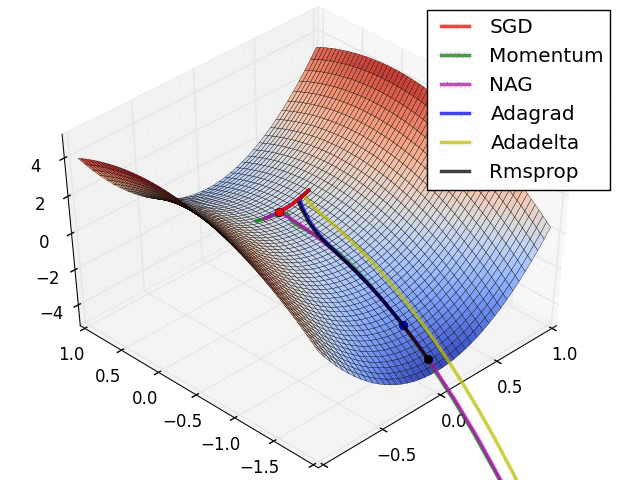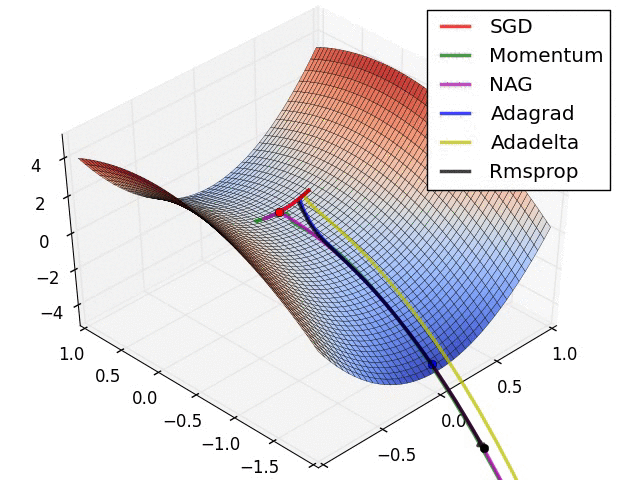
위의 사이트를 가보면 다양한 Optimizer들이 어떻게 최솟값을 찾아가는지 눈으로 확인할 수 있다.
Optimizer 종류는 굉장히 다양하다

이번 설명에서 쓸 Optimizer인 경사하강법의 원리를 설명한 사진은 다음과 같다.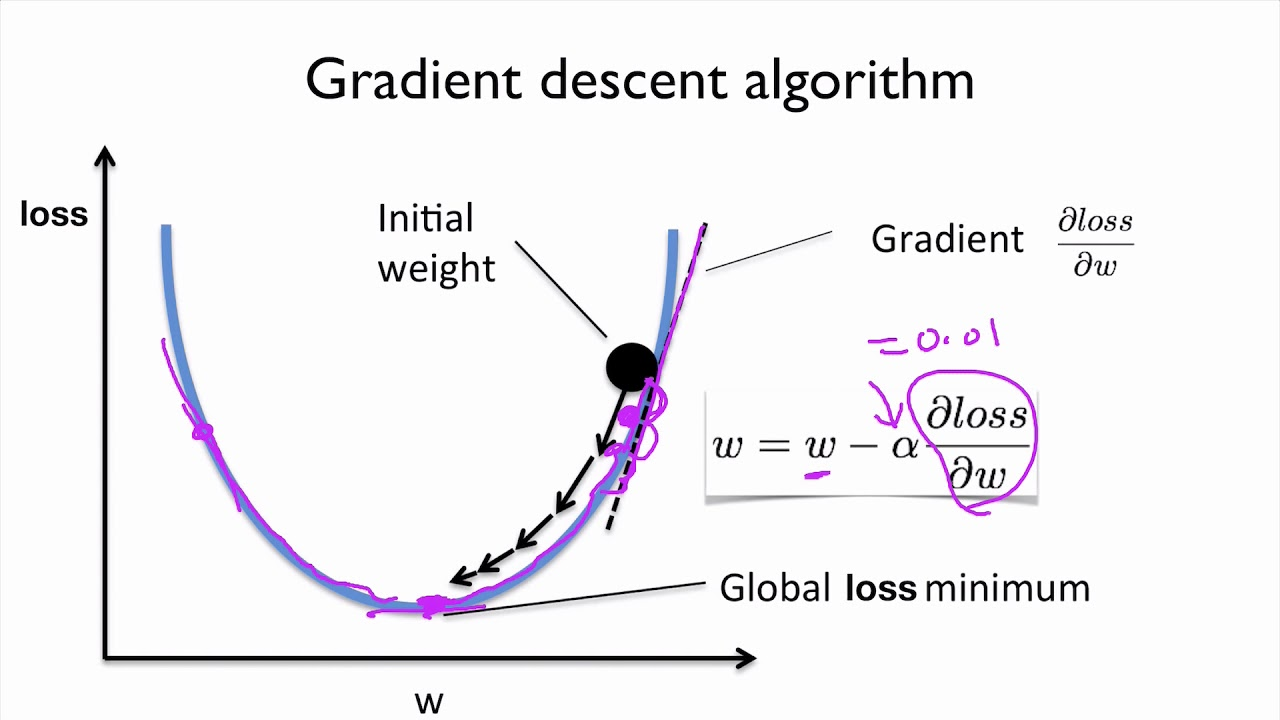

경사하강법은 너무나 중요하지만 이번 시간에 다룰 주제는 아니기 때문에 꼭 다른 자료를 참고해서 공부하길 바란다.

그림을 보면 알 수 있듯이 loss 함수의 최솟값을 찾기 위해서는 w값을 조절해야한다. 왜냐하면 가중치와 편향값만이 우리가 "조절"할 수 있는 변수들이기 때문이다.

위의 사진을 참고하면 이제 이 수식을 사용하는 이유를 알 수가 있다.

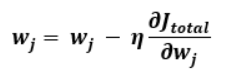
은닉층 단계에서 정확히 어떤 값을 가져야하는지는 모르지만, 우리 모두는 loss function이 최솟값을 가지길 원한다. 따라서 조절 가능한 변수인 가중치 값들은 손실 함수가 최솟값을 가지도록 조절되어야 하고, 우리는 각 층의 모든 노드들에서의 가중치 값을 update할 수가 있다.

결국 심층 신경망 학습에서는, 역전파 알고리즘에 쓰이는 그레디언트 계산을 효과적으로 할 수 있는 알고리즘이 곧 얼마나 신경망을 효과적으로 학습시킬 수 있을지를 결정하는 핵심적인 요소가 되게 되는 것이다.

https://www.youtube.com/watch?v=tIeHLnjs5U8
위의 과정을 시각적으로 너무나 잘 표현해준 유튜브이다. 1~4편의 시리즈로 구성되어 있는만큼 모든 편을 꼭 다 보도록 하자. 어떤 자료보다도 도움이 될 것임을 확신한다.

정리

입력 값(leaf라고 부름 pytorch에서는)을 입력층에 입력

다음 은닉층의 w값과 입력값들이 선형 결합의 꼴을 이루고, b도 더함. 이걸 z라고 하자. 참고로 b는 편향 값으로, 얼마나 뉴런이 활동적인지를 판단하는 척도.

z는 이제 활성화 함수를 거쳐야함 sigmoid함수(얘는 너무 값이 작아서 은닉층에서는 잘 안써) or ReLu 알고리즘 이용

z가 활성화 함수를 거친 값을 a라고 하면, 또다시 a값이 다음 층에 대해 입력값 역할을 하게 되고 2-3번의 과정을 반복한다.

최종 출력층에서 실제 데이터 값과 비교를 한 뒤, 역전파 알고리즘을 통해 가중치 값 업데이트

오차가 허용 범위 안에 들어올 때 까지 1~5번 과정 반복

Pytorch를 이용한 역전파 알고리즘 코드

Pytorch로 시작하는 딥러닝 입문 참조(MNIST 예제)

%matplotlib inline
import matplotlib.pyplot as plt # 시각화를 위한 맷플롯립
from sklearn.datasets import load_digits

import torch
import torch.nn as nn
from torch import optim

digits = load_digits() # 1,979개의 이미지 데이터 로드

images_and_labels = list(zip(digits.images, digits.target))
# for index, (image, label) in enumerate(images_and_labels[:5]): # 5개의 샘플만 출력
#     plt.subplot(2, 5, index + 1)
#     plt.axis('off')
#     plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
#     plt.title('sample: %i' % label)

X=digits.data # 8x8 행렬을 64차원의 벡터로 변환
Y=digits.target

model = nn.Sequential(
    nn.Linear(64,32), # input_layer = 64, hidden_layer1 = 32
    nn.ReLU(),
    nn.Linear(32,16), # hidden_layer2 = 32, hidden_layer3 = 16
    nn.ReLU(),
    nn.Linear(16,10) # hidden_layer3 = 16, output_layer = 10
)

X=torch.tensor(X,dtype=torch.float32)
Y=torch.tensor(Y,dtype=torch.int64)

loss_fn = nn.CrossEntropyLoss()

optimizer = optim.Adam(model.parameters())
losses = []

for epoch in range(100):
  optimizer.zero_grad() #경사를 0으로 초기화
  y_pred = model(X) # forward 연산
  loss = loss_fn(y_pred, Y)
  loss.backward()
  optimizer.step() # 역전파 계산 과정에 따라 가중치 값 수

  if epoch % 10 == 0:
    print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, 100, loss.item()
        ))

  losses.append(loss.item())

plt.plot(losses)