Weierstrass Approximation Theorem

• 연속 함수가 주어진 구간에서 다항식의 극한으로 근사 가능하다.
• 예를들어, sin(27.2)와 같은 값을 다항식의 극한으로 표현하여 근사가 가능하다.

Taylor series

• 특정 함수 f(x)를 특정 점 a에서 함수값과 도함수들을 이용하여 다항식으로 근사하는 방법이다.
• 이 다항식은 함수의 주변에서만 잘 근사되며, 즉, 일반적으로 특정 점에서의 근사가 잘 이루어진다.
  • Weierstrass 근사 정리의 특수한 사례로 볼 수 있다.

예시

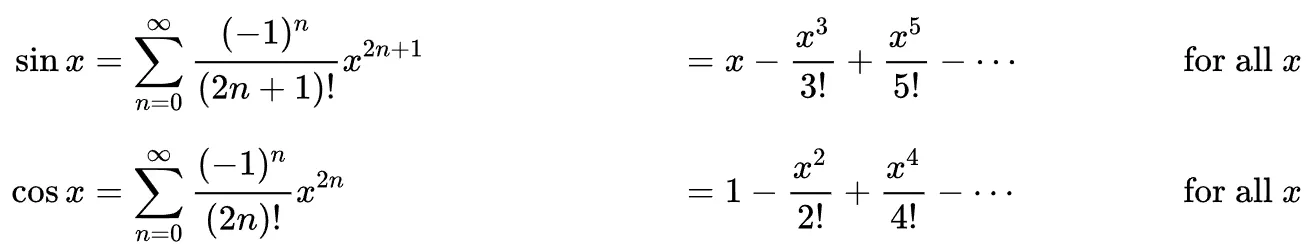
• sin(x) , cos(x)의 경우, Taylor series에 따라 위와 같이 다항식의 극한으로 표현가능하다.
• 위의 경우 a = 0인 매클로린 급수(Maclaurin series)이다.

MATLAB 예시

syms x
f = sin(x)/x;
T6 = taylor(f, x, 'Order', 8);
pretty(T6)

• syms : MATLAB에서 심볼릭 변수를 정의하는 명령어이다. 수치적 계산이 아닌 수학적 기호를 사용하여 수식을 표현할 때 사용한다. (Symbolic Math Toolbox 설치가 필요)
  • 즉, x는 수치적 계산이 아니라 기호적 계산에 사용한다.
• taylor() : 심볼릭 수학에서 주어진 함수의 Taylor Series를 구하는 함수
• pretty() : 수식을 보기 좋은 형태로 출력하는 함수

💡 심볼릭 수학 : 수치 계산과 달리 기호를 사용하여 수학적 표현을 정확하게 다루는 방식

• 함수, 방정식, 미분, 적분 등을 숫자 값으로 계산하는 대신, 수학적 기호와 식을 그대로 유지하여 처리하는 수학적 접근법을 의미

Taylor series 근사

x = -10:0.01:10; 
y = 0;
for n = 0:10
    % 실제 함수 그리기
    plot(x, sin(x), 'r', 'linewidth', 2, 'DisplayName', 'sin(x)');  % sin(x)
    % plot(x, cos(x), 'r', 'linewidth', 2, 'DisplayName', 'sin(x)'); % cos(x)
    hold on;
    
    % Taylor 급수로 근사한 y 계산
    y = y + ((-1)^n / factorial(2*n+1) * (x.^(2 * n + 1))); % sin(x)
    % y = y + ((-1)^n/factorial(2*n) * (x.^(2 * n))); % cos(x)
    
    % 근사 함수 그리기
    plot(x, y, 'b', 'DisplayName', ['Taylor Approx (n = ' num2str(n) ')']);
    
    % 축 및 범례 설정
    axis([-10 10 -2 2]);
    legend('show'); % 범례 표시
    pause(0.5); % 잠시 멈춤
    hold off;
end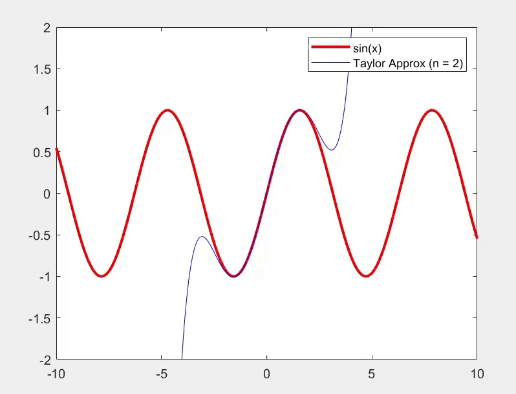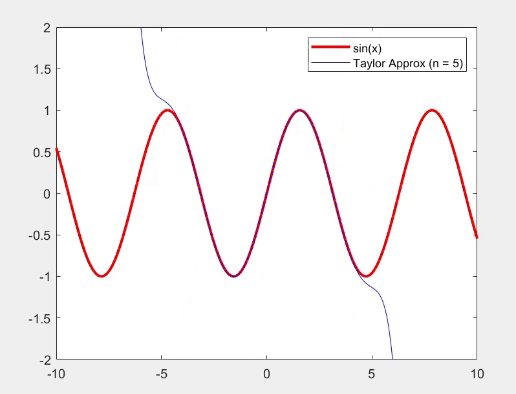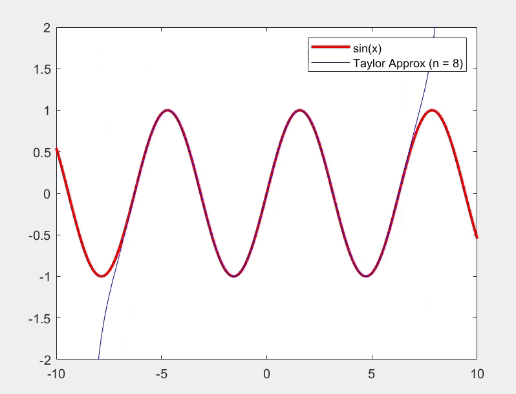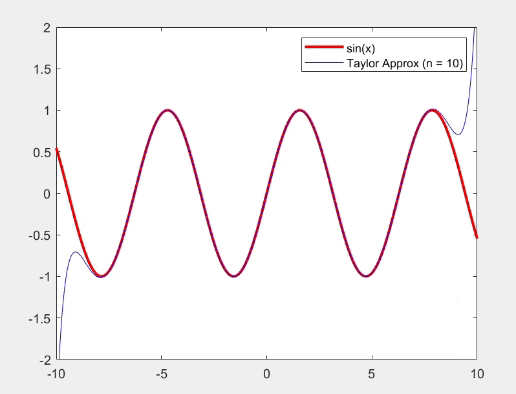

• sin(x)와 cos(x)에 대해 Taylor series를 사용하여 근사하고, 원래 함수와 비교하는 그래프를 생성한다.
• 적은 항으로도 함수의 특성을 일부 근사할 수 있지만, 많은 항을 추가할수록 정확도가 높아짐을 알수 있다.

Universal Approximation Theorem

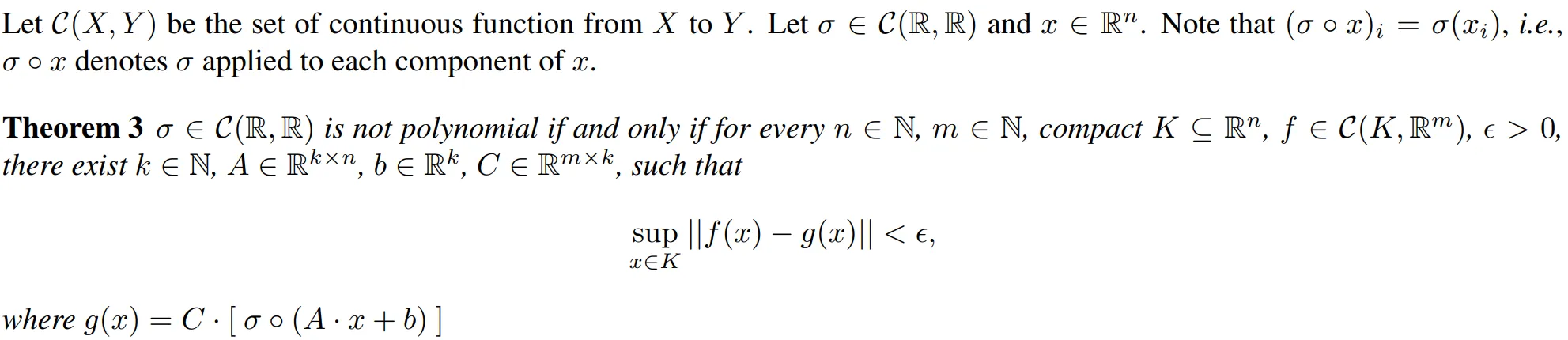
• Universal Approximation은 Weierstrass Approximation의 아이디어를 신경망으로 확장하여, 다차원 데이터와 딥러닝의 복잡한 함수 근사 문제를 해결할 수 있도록 일반화한 상위 개념
• 모든 연속 함수 f∈C(K, Rm)는 적당한 심층 신경망 구조로 작은 오차 내에서 근사 가능하다.
  • 모든 연속 함수는 적절한 활성화 함수를 사용하는 신경망으로 근사 가능하다.
• 조건
  • 활성화 함수 σ∈C(R,R)가 다항식이 아니어야 한다.
    • 예: sigmoid, ReLU, tanh 등은 조건을 만족함
  • 이를 만족할 경우, 심층 신경망의 매트릭스와 벡터 A, b, C를 적절히 설계하여  *f(x)≈C⋅[σ∘(A⋅x+b)]로 표현 가능하다.
• 핵심
  • 심층 신경망은 충분히 복잡한 구조를 통해 다차원 연속 함수를 근사할 수 있다.
  • 딥러닝에서 활성화 함수의 비선형성이 신경망이 복잡한 함수를 근사하는 데 필수적이라는 점을 강조한다.
  • 모든 연속 함수를 근사 가능함을 이론적으로 증명한다.