푸리에 급수(Fourier series)

• 주기함수를 삼각함수(cos()과 sin())의 합으로 표현하는 수학적 방법이다.
  • 모든 주기 함수가 삼각 함수의 선형 결합으로 표현 가능하다는 사실을 보여준다.
• 주기적인 현상을 분석하거나 근사할 때 사용된다.
• 참고 링크 : 위키피디아 푸리에 급수
  

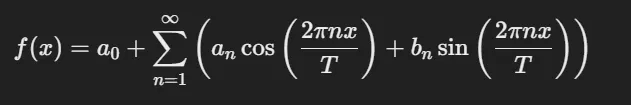
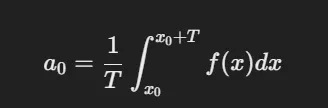
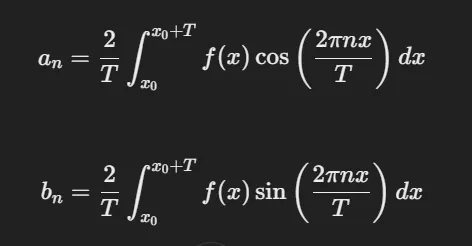
T = 2π인 경우 주기함수

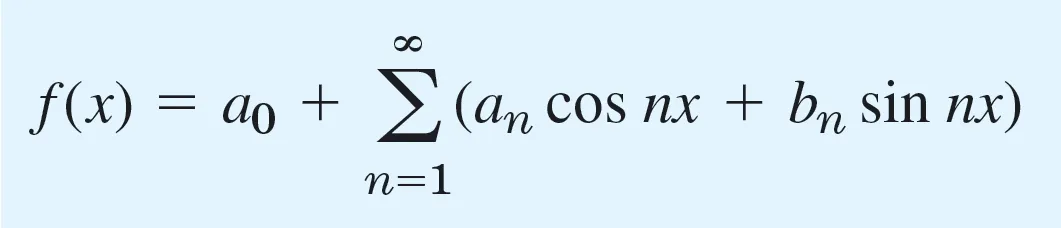
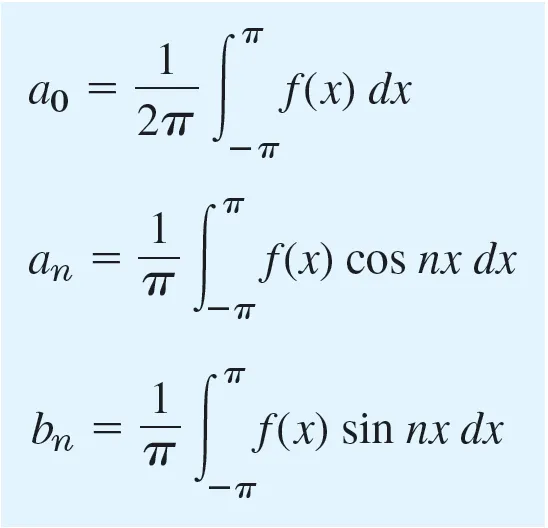
예시

함수 1 - 주기(T)가 2π

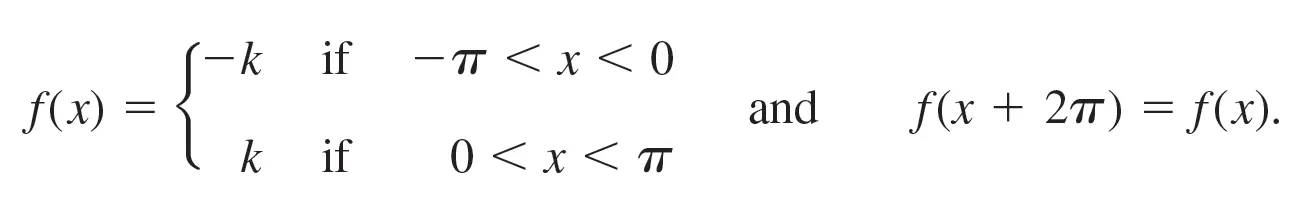
• 위와 같은 2π 간격의 주기함수를 푸리에 급수를 이용하여 표현할 수있다.

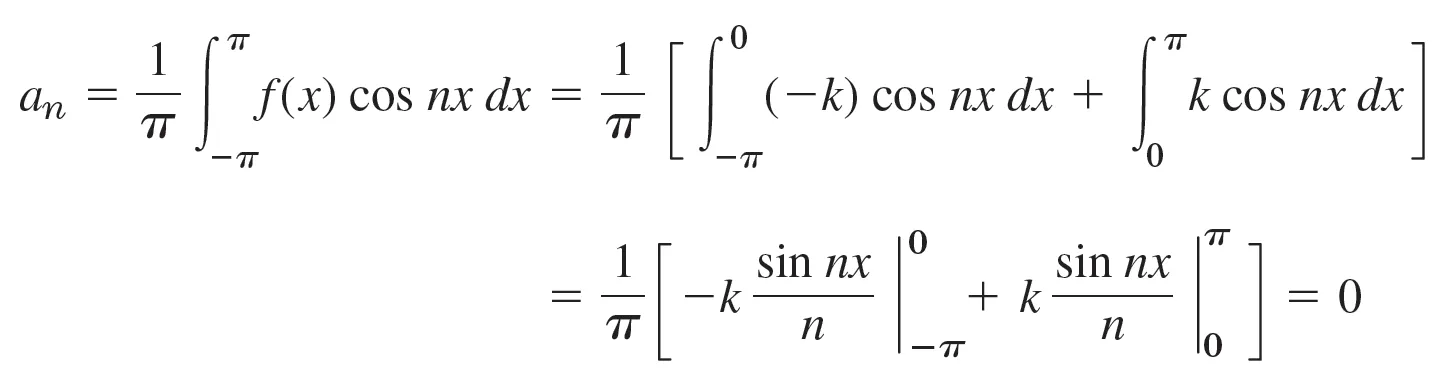
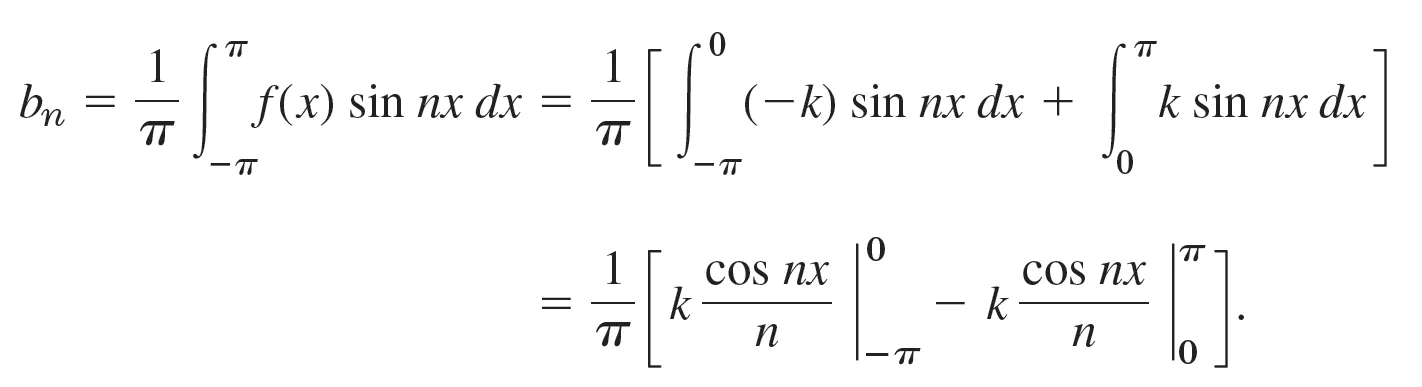
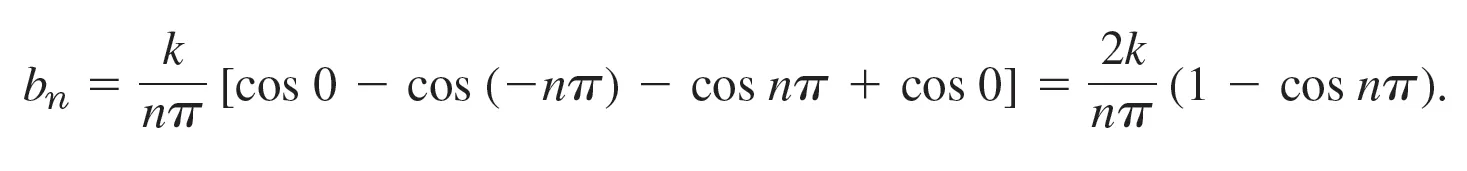
• 따라서 푸리에 급수식에 따라 aₙ과 bₙ을 전개하면 위와 같다.

MATLAB 예시

k = 2;
line([-pi 0], [-k -k]); hold on; line([0 pi], [k k]);
axis([-4 4 -3 3])

x = -pi:0.01:pi; a0 = 0; fs = a0;

for n = 1:20
    fs = fs + 0*cos(n*x) + (2*k / (n * pi) * (1 - cos(n*pi)) * sin(n*x));
end
plot(x, fs, 'r')

n = 20

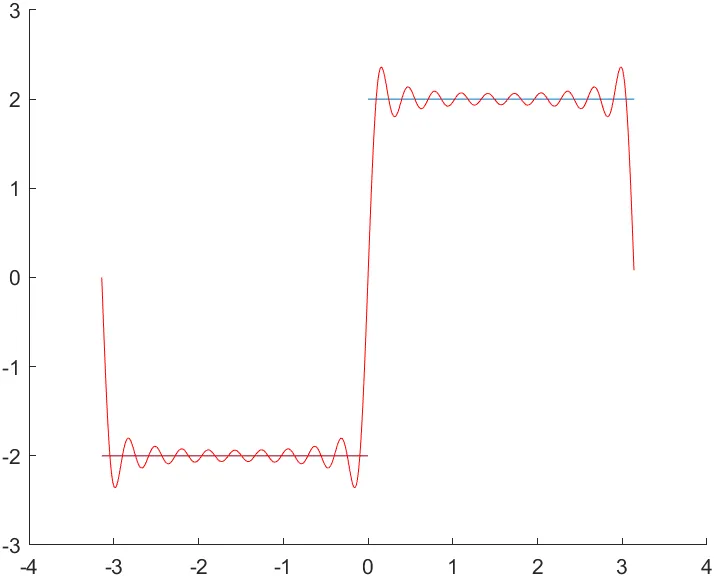
n = 300

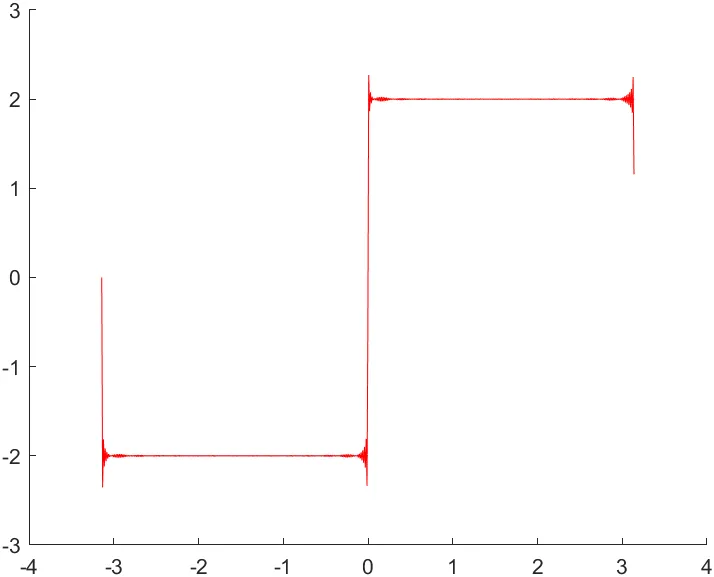
• n의 범위가 커질수록 Fourier 급수가 주기 함수에 더 가까워져, 원래 함수의 형태를 점점 더 정확히 근사할 수 있음을 확인할 수 있다.

함수 2 - 주기(T)가 4

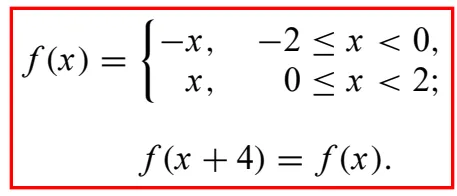
• 위와 같은 4 간격의 주기함수 또한 푸리에 급수를 이용하여 표현할 수있다.

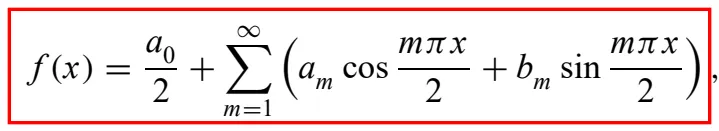
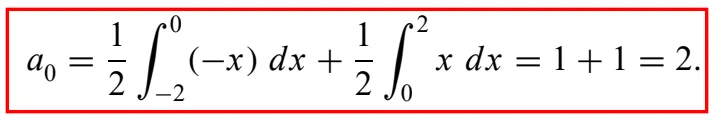
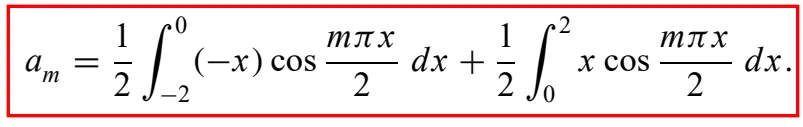
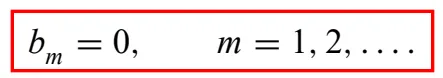
MATLAB 예시

k = 2; 
line([0 k], [0 k]); hold on; line([-k 0], [k 0]);
axis([-k k -1 3])

x = -k:0.01:k;
a0 = 2; fs = a0/2;
for n=1:20
	if mod(n, 2) == 0
		an = 0;
	else:
		an = -8/(n*pi)^2);
	end
	fs = fs + an * cos(n*pi*x/2) + 0*sin(n*pi*x/2)
end

plot(x, fs, 'k')
hold off

확대한 그림

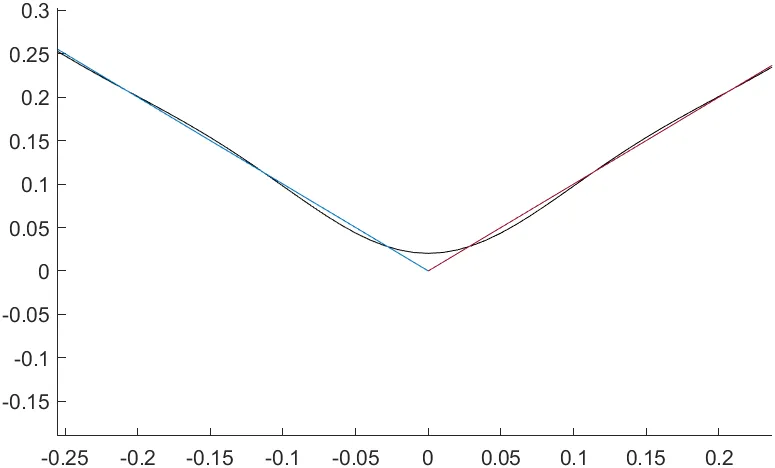
• 검정색  Fourier 급수가 주기 함수에 더 가까워져, 원래 함수의 형태를 근사한다.