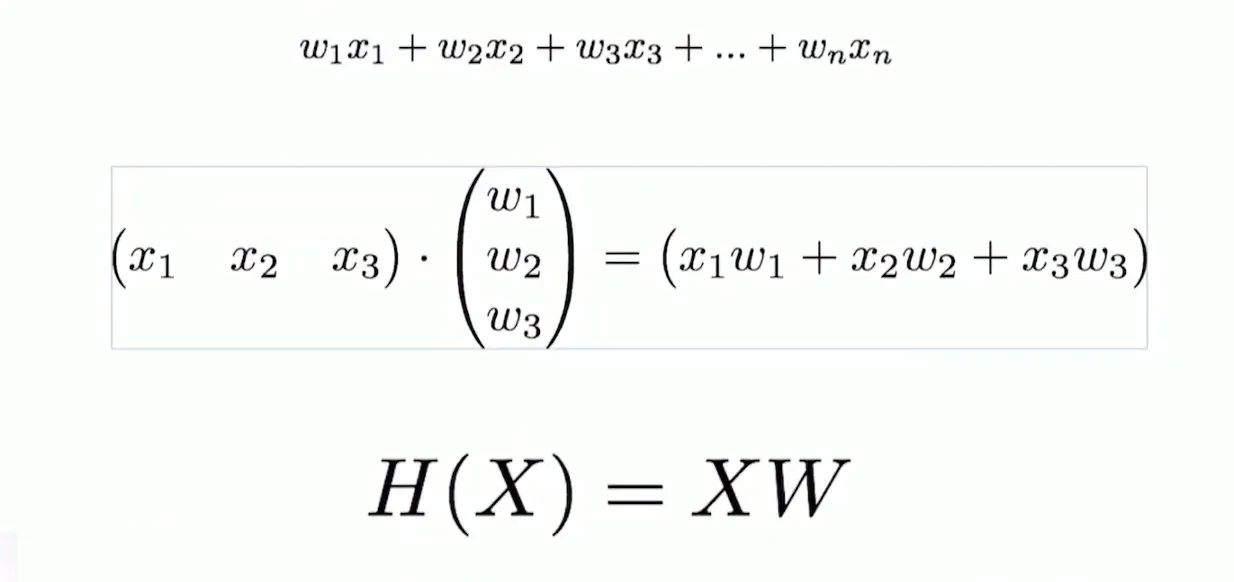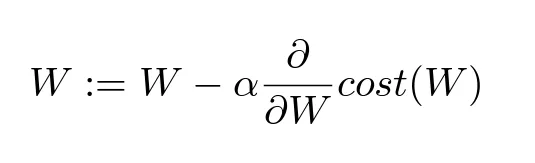이 블로그글은 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 2019년 딥러닝 홀로서기 세미나 영상을 수강하고 작성한 글임을 밝힙니다.

Linear Regression

Regression

• 입력 변수(특성, 독립 변수)와 출력 변수(목표 변수, 종속 변수) 간의 관계를 모델링하는 예측 분석 기법
• 회귀의 목표는 연속적인 숫자 값을 예측하는 것이며, 주어진 데이터를 기반으로 변수 간의 관계를 분석하고, 그 관계를 바탕으로 미래의 값을 예측하는 데 사용

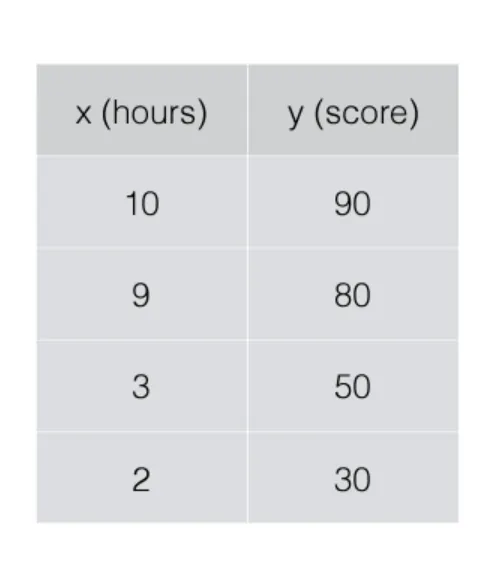
Linear Regression

• 데이터를 가장 잘 표현하는 선형 가설(Linear Hypothesis)을 찾는 것

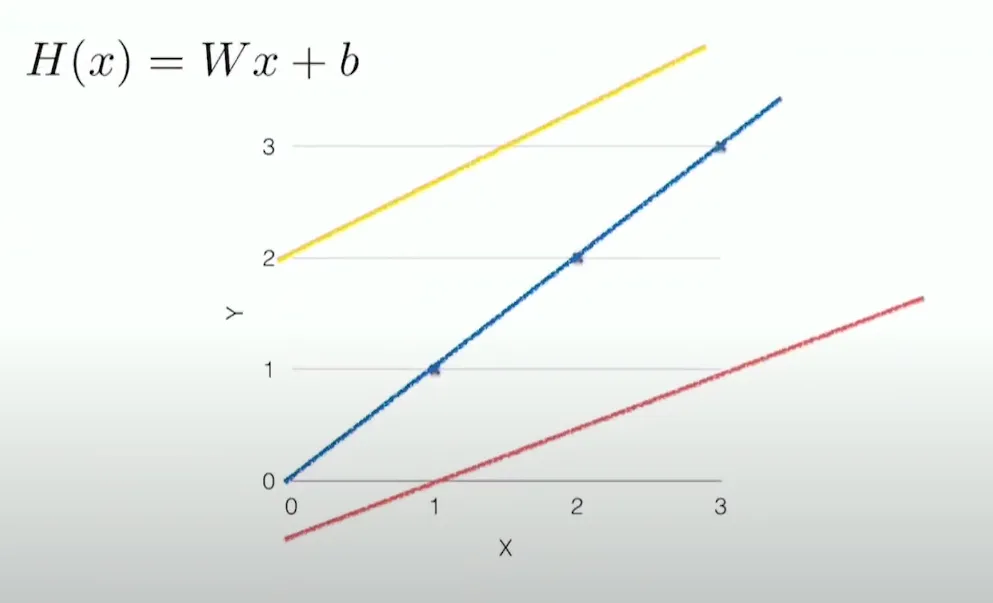
→ 어떻게 찾는게 좋을까?

• 실제 데이터와 예측데이터 사이의 거리를 계산

Cost function

• 가설이 ‘좋냐? 나쁘냐?’를 정량화하는 지표
• Loss function이라고도 부름

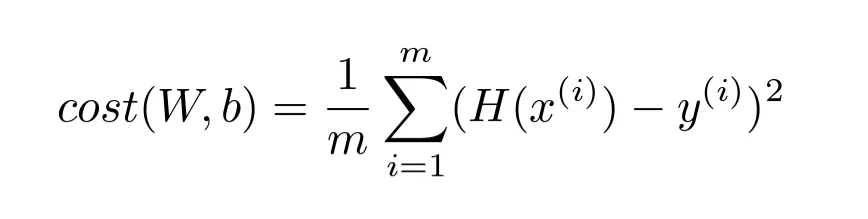
Goal

• Cost function을 최소화하는 가중치 W와 편향 b를 찾는 것

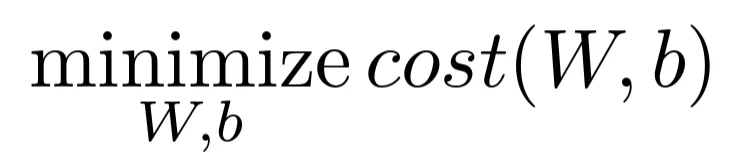
Simplified hypothesis

• 편향 b를 가중치 W의 한 요소로 포함시켜, 가설을 간단하게 표현할 수 있습
  • 입력 벡터 x에 추가적인 차원을 넣어서 편향을 가중치와 함께 처리할 수 있다는 것을 의미

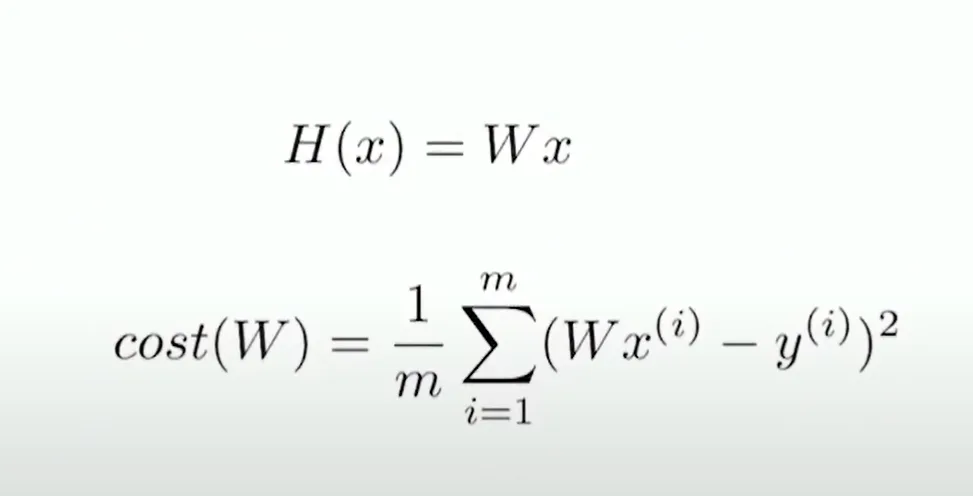
Cost를 어떻게 최소화 할 수 있을까?

• W = 1, cost(W) = 4.67
• W = 0, cost(W) = 0
• W = 2, cost(W) = 4.67

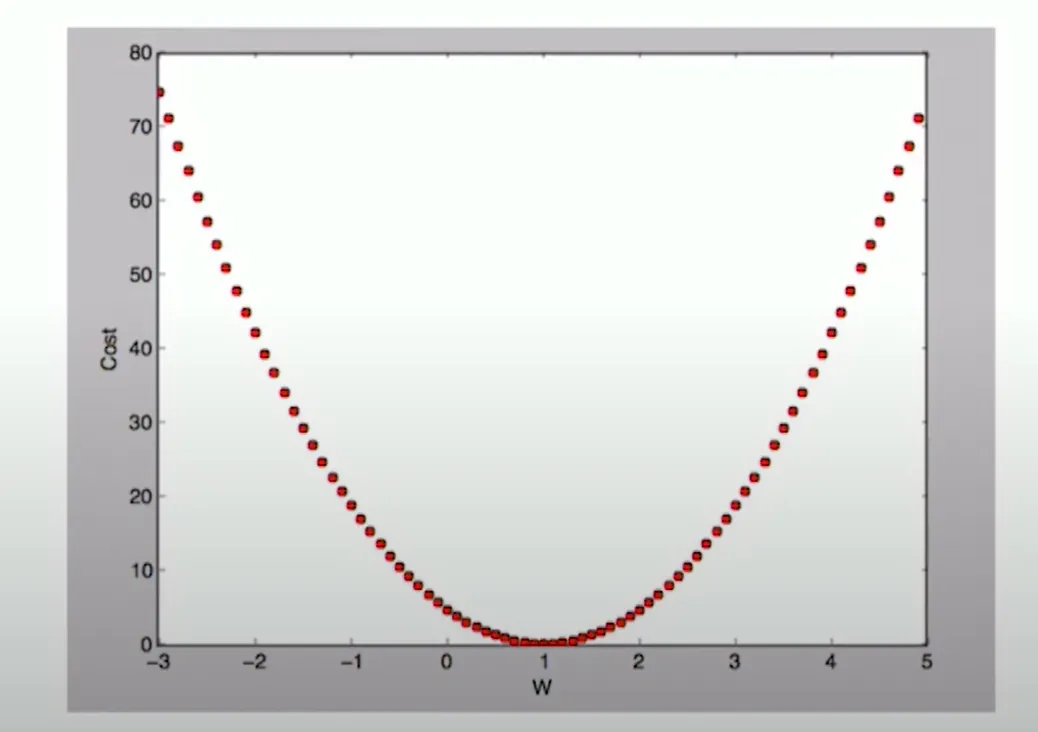
• 이 경우, cost function 시각화를 했을때 W가 1일때 Cost가 가장 작음을 알 수 있다.

→ 실제로는 가중치의 차원이 크기 때문에 cost function을시각화하기 어렵다는 어려움

Gradient descent algoritm

• cost function을 최소화하는 알고리즘

방법

1. 초기 추정값으로 시작하기 : (0, 0)에서 시작하거나, 다른 임의의 값에서 시작할 수 있습니다.
2. W와 b를 조금씩 변경하면서 cost function Cost(W, b)를 줄이는 방향을 찾음
3. 매번 파라미터를 변경할 때마다 cost function Cost(W,b)를 가장 많이 줄일 수 있는 방향, 즉 기울기(gradient)를 선택
4. 1 ~ 3 번 과정을 반복 : 비용 함수가 더 이상 크게 변하지 않을 때까지 반복
   • 즉, 지역 최소점에 수렴할 때까지 계속합니다.

• (참고) 시작하는 위치에 따라 도달하는 최소점이 달라질 수 있음

Gradient descent algoritm 수식

• 여기서 α는 학습률(learning rate)
  • learning rate : 머신러닝 모델이 가중치를 업데이트할 때 사용하는 비율로, 모델이 데이터를 학습하는 속도를 조절

Convex function

• Gradient descent algorithm의 경우 초기값을 어디로 선택하냐에 따라 지역최소점에 빠질 수 있음
  • 5번 random으로 실행하여 평균을 내는 방법을 사용하기도 함
    

Multivariable Linear Regression

• 입력변수 x가 2개이상인 경우 사용하는 회귀 기법

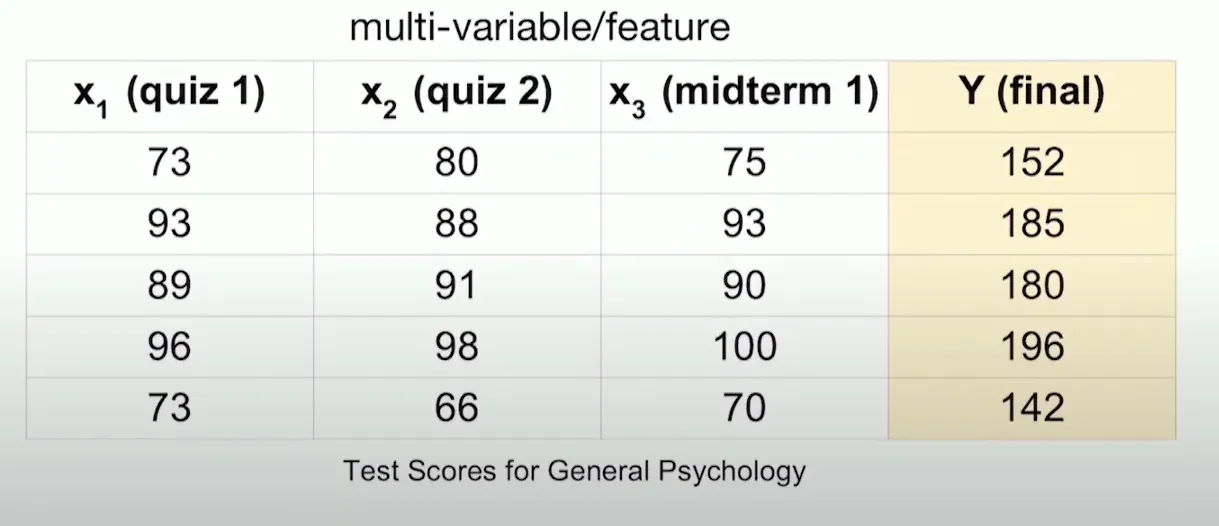
Cost function

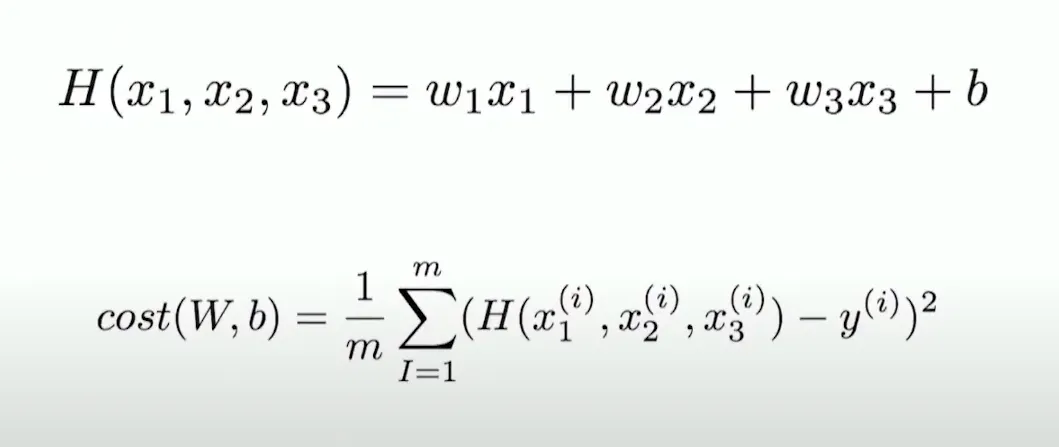
Hypothesis using matrix

• matrix 형태로 표현이 가능
  • matrix 형태로 표현하면, 여러개의 데이터에 대한 표현도 편해짐 (numpy 사용)