이 블로그글은 2019년 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 딥러닝 홀로서기 세미나를 수강하고 작성한 글임을 밝힙니다.

Binary / Multi-label Classifciation

Binary Classification

• 이산적인 데이터를 다루는 Supervised Learing 문제이다.
• 특히 분류해야할 클래스가 두 가지인 경우가 Binary Classifciation 이다.

→ 각각을 0과 1로 encoding할 필요가 있다.

Hypothesis

• Study Hours에 따른 Pass(1)/Fail(0) 문제가 예가 될 수 있음
• Linear Regression Hypothesis를 적용해서 문제를 풀 수 있을까?
  • 새로운 데이터로 모델이 변하여 잘못 분류가 일어날 수 있음
  • Continuous한 값이므로 0보다 작거나 1보다 큰값이 나올 수 있음

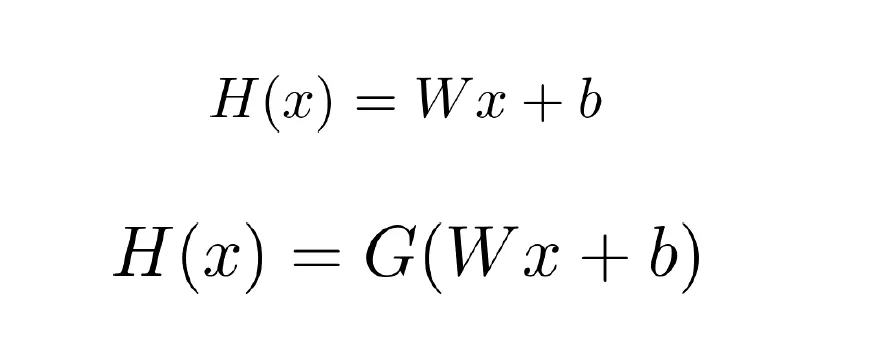
→ Linear Regression Hypotheis에 적절한 함수를 적용해서 Binary Classifciation Hypothesis를 정의하자.

Sigmoid (Logistic) Function

• 전체 값에 대해 0과 1 사이에 대응됨.

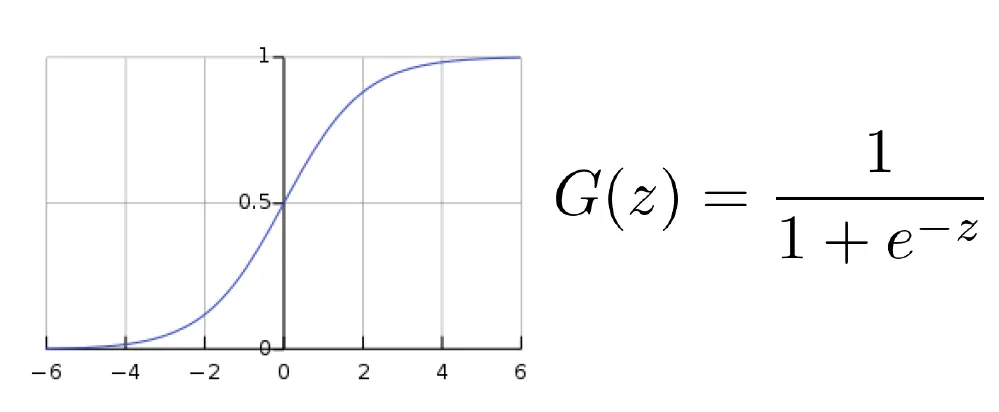
Logisitc Hypothesis

• linear Regression Function을 sigmoid (Logisitic) Function 함수를 적용

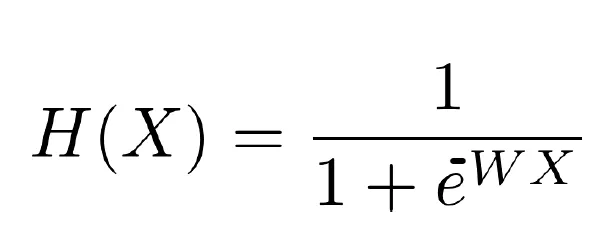
Cost Function

• Linear Regression에서 썼던 cost function을 그대로 사용하면 되지 않을까?
  • 그래프를 그려보면 saddle point가 많음을 알 수 있음
  • trainning을 계속해도 학습해도 학습이 되지 않고 local minimum에 갖혀버리게 됨

💡 saddle point (안장점)
함수의 기울기가 0이지만, 최소값이나 최대값이 아닌 지점으로, 한 방향에서는 함수값이 증가하고 다른 방향에서는 감소하는 지점

Cross Entropy

• 두 확률 분포의 차이를 측정하는 지표
  • P(x) : 실제확률
  • Q(x) : 예측확률
  • 예측이 정확할수록 값이 작아지고, 예측하기 어려울수록 값이 커짐.

💡 Entropy(엔트로피)
어떤 일이 일어날지 예측하기 어려운 정도를 나타내는 값
사건들이 모두 비슷한 확률로 일어나면 엔트로피는 높고, 어떤 사건이 일어날 가능성이 훨씬 크면 엔트로피는 낮아짐

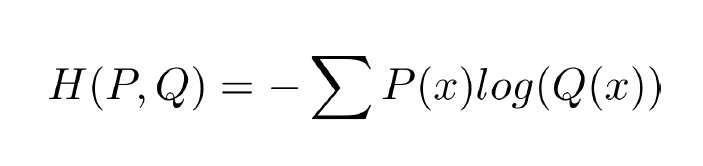
Cost Function

• 각 데이터의 cost를 계산하고 평균을 낸 것
  • y = 1인 경우 -log(H(x))
    • 예측이 1에 가까운 경우 값이 작아짐
    • 예측이 0에가 까운 경우 값이 커짐
  • y = 0이니 경우 log(1 - H(x))
    • 예측이 0에가 까운 경우 값이 작아짐
    • 예측이 0에가 까운 경우 값이 커짐

→ 즉 잘 예측한 경우 값이 작아지고 예측을 잘못하면 값이 커짐

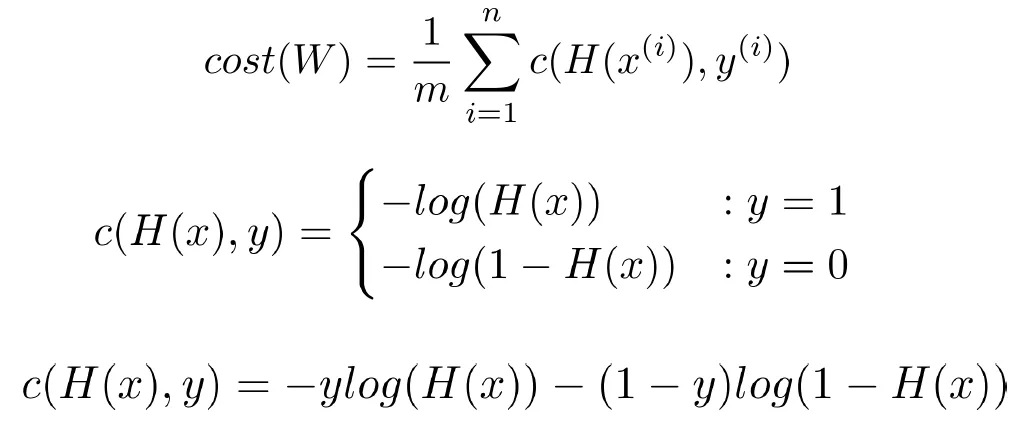
→ 학습 할때는 역시 Gradient descent 알고리즘을 사용함

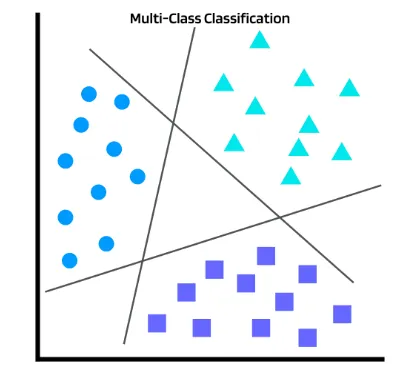
Multinomial Classification

• 분류해야할 클래스가 3개 이상인 경우
• Binary Classifcation에서 사용한 Hypothesis를 사용하면 되지않을까?
  • Sigmoid 함수는 0과 1 사이의 값만을 출력하므로 3개 이상인 다중 분류 문제에서는 사용할 수 없음

Hypothesis

• Binary Classification의 Hypothesis 함수처럼 Linear Regression 함수에 특정 함수를 적용하면 해결할 수 있지 않을까?

→ Softmax 함수를 적용

Softmax function

• 각 클래스에 대응될 확률을 출력하는 함수
• 0 ~ 1사이의 값을 가짐

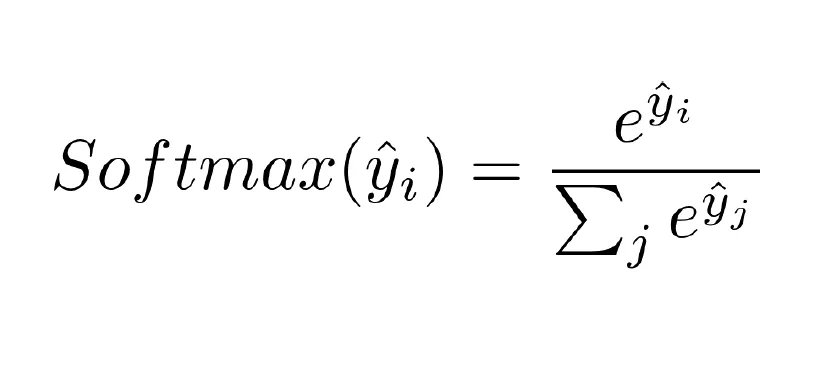
Cost function

• 각 클래스마다 Cross entropy의 값을 더하여 계산
  

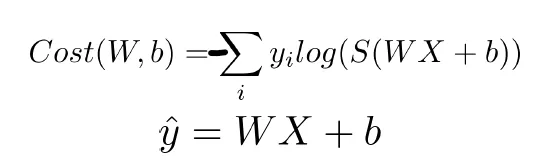
→ 학습 할때는 역시 Gradient descent 알고리즘을 사용함