[Linear Equation] Vector Equations

vectors in R2

연산
1. vector summation

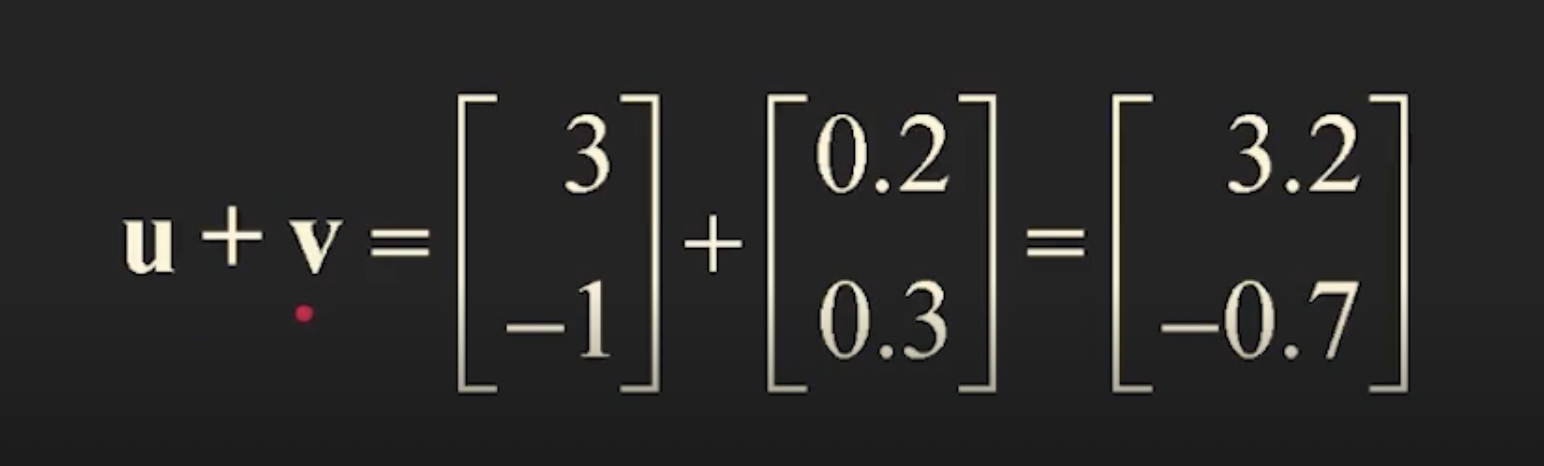
2. scalar multiplication

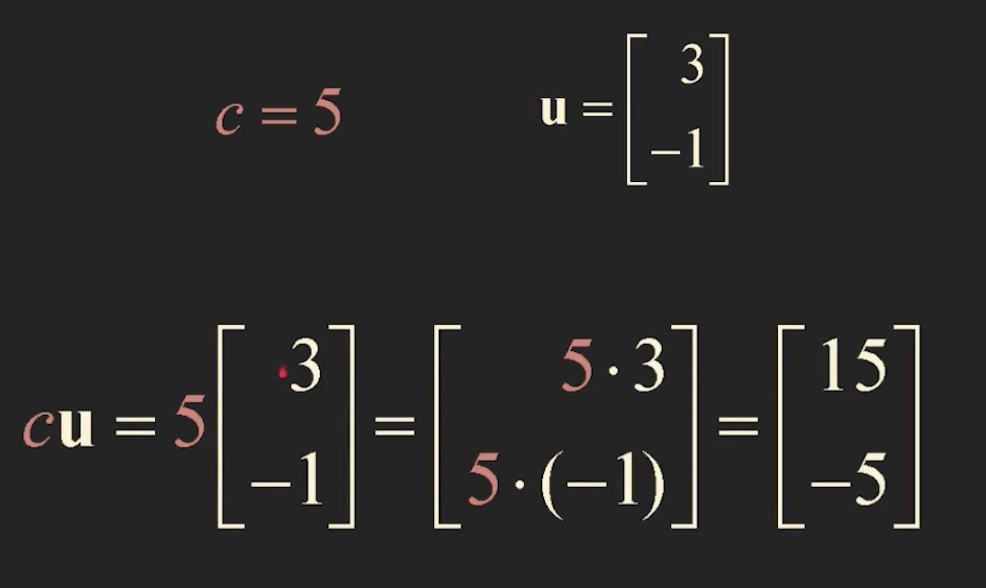
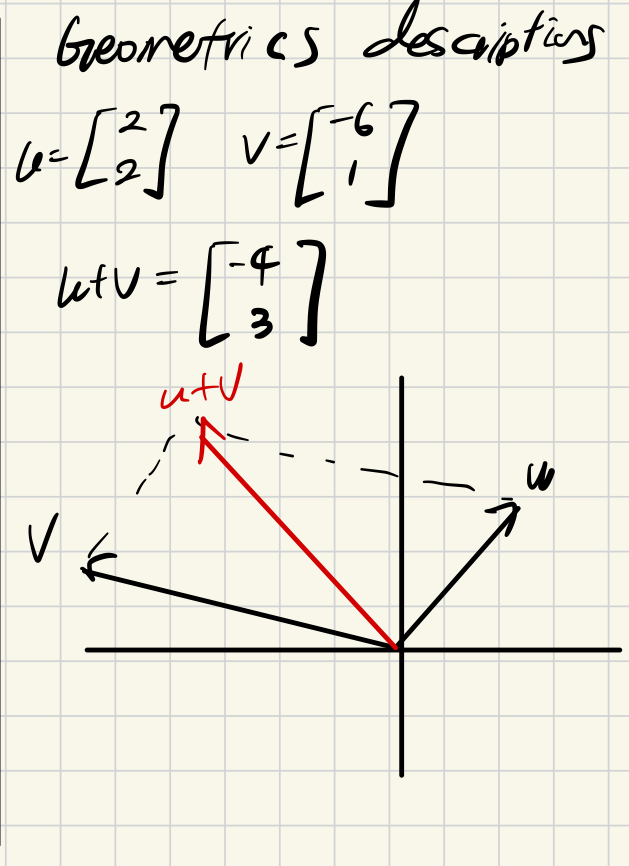
3. geometrics descriptions of vectors

vectors in Rn

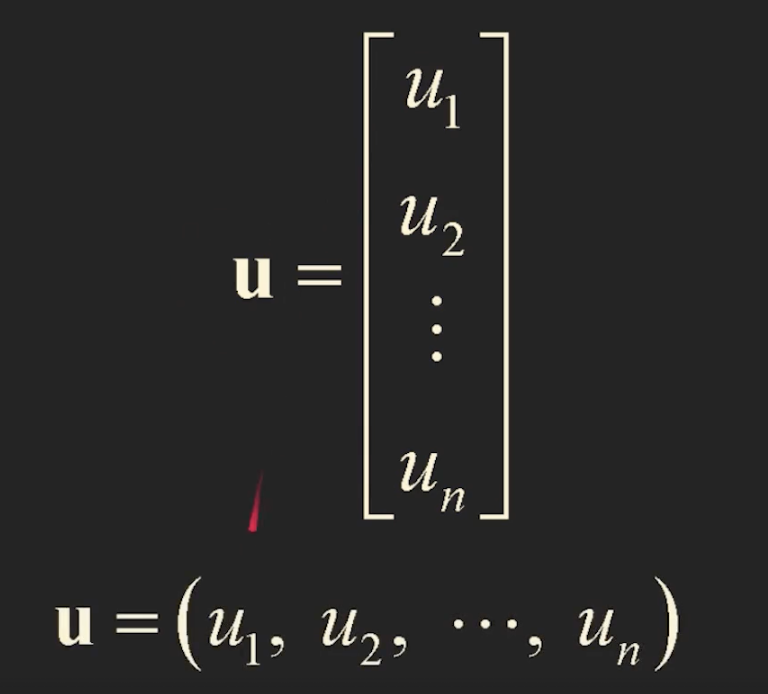
Algebraic properties of Rn

u,v,w -> Rn (Vector)
c,d -> scalar
i) u + v = v + u
ii) (u+v) + w = u + (v+w)
iii) u + 0 = 0 + u = u
iv) u+(-u) = -u+u = 0
v) c(u+v) = c_u + _c_v
vi) (_c+d)u = c_u + _d_u
vii) _c(d_u) = (_cd)u
viii) _1_u = u

Linear combinations

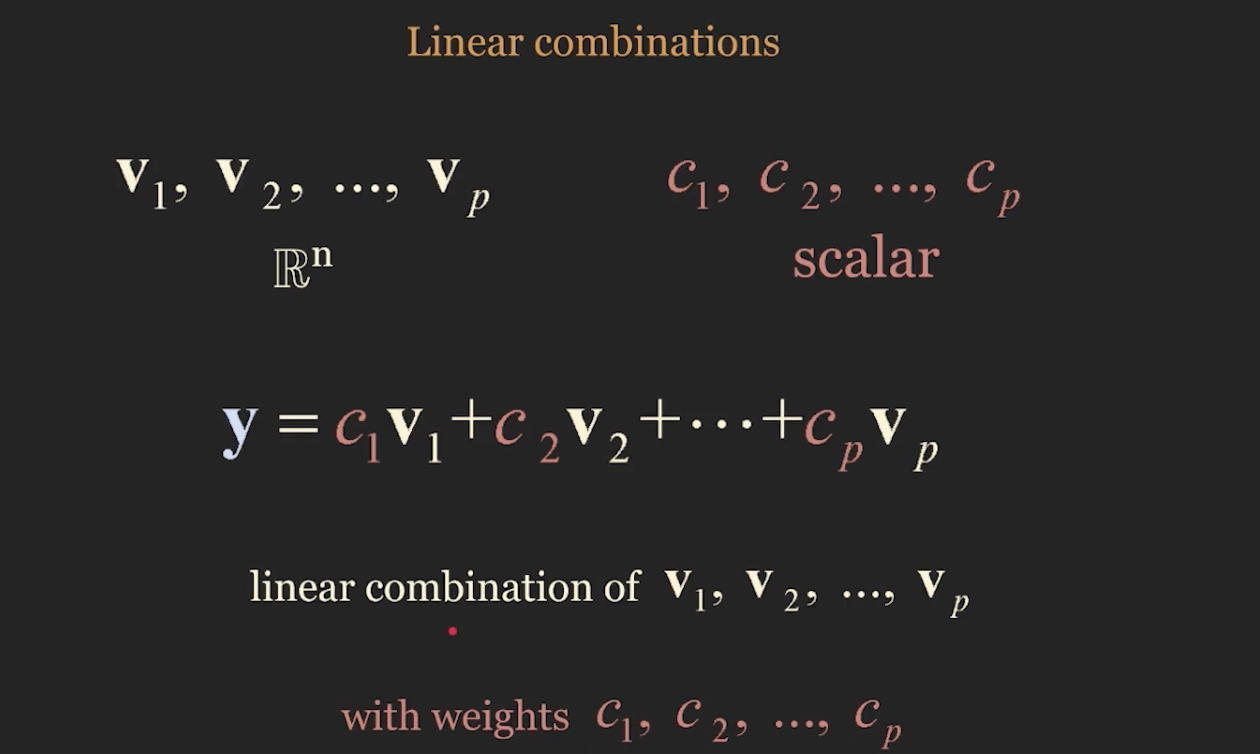
• linear combination의 예제
  augmented matrix 형식처럼 풀면됨

Span{v₁, ..., vₙ}:

벡터 v₁, ..., vₙ을 아무 숫자(x₁, ..., xₙ)로 곱해서 더해 만든 모든 벡터들의 집합
-> 즉, "v₁~vₙ을 조합해서 만들 수 있는 벡터들"

• Is a vector b in Span{v1,...,vp}?

• does the following vector equation have a solution ?
  x1v1+ x2v2+ ... xnvn = b

• does the following augemented matritx have a solution ?
  [v1,... vn b]

-> 세 질문 모두 "벡터 b가 v₁, ..., vₙ의 선형결합으로 만들어질 수 있냐?"를 묻는 문제

Span{u}={x⋅u∣x∈R}

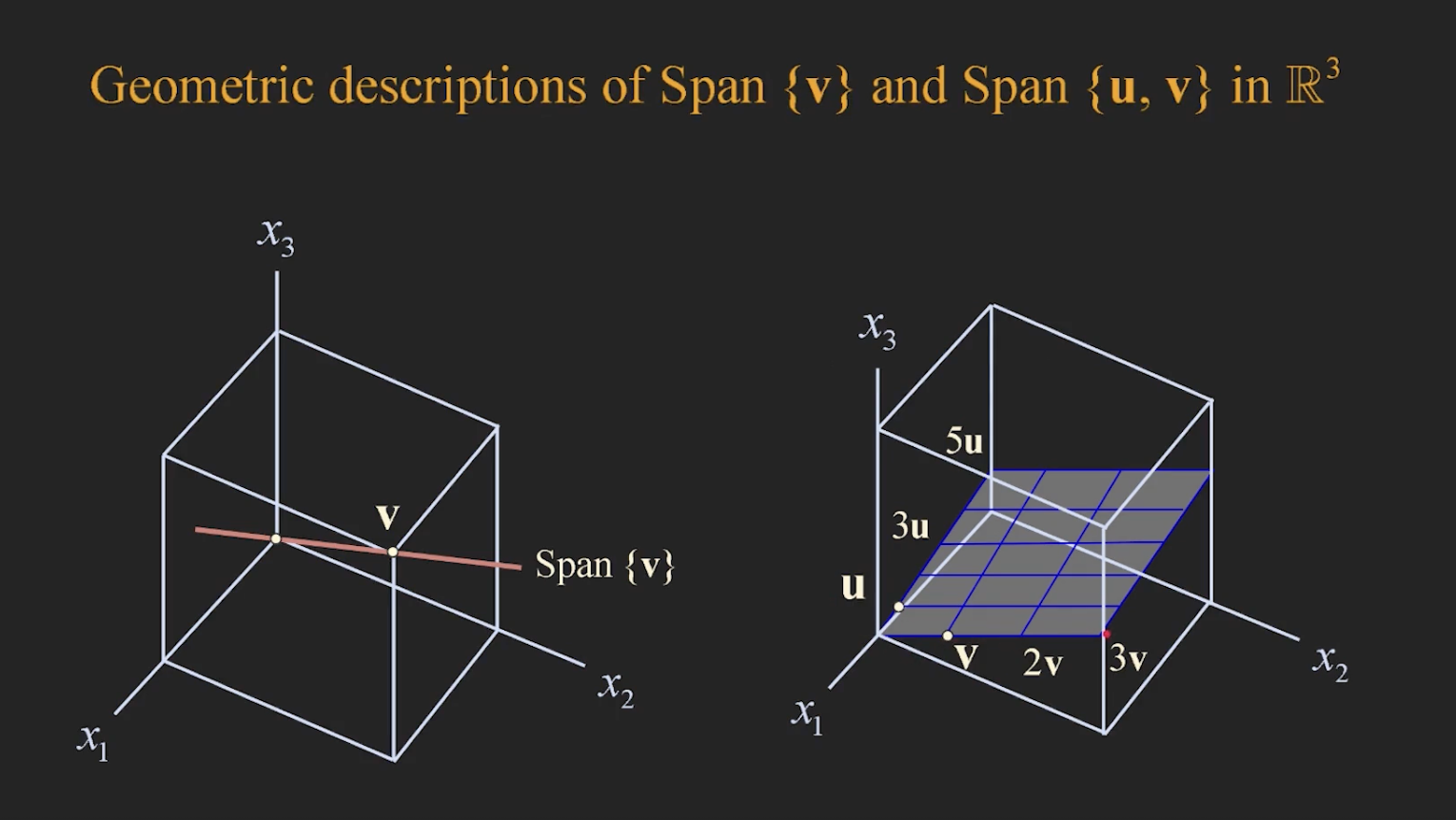
Span 형태	벡터 수	결과 형태	예시
Span{v}	1개	직선	$x \cdot v$
Span{u, v}	2개	평면	$x \cdot u + y \cdot v$