[Linear Equation] Row Reduction and Echelon Forms

A nonzero row or column

• matrix에서 특정 row 나 column에서 최소 0이 하나 있으면 됨

A leading entry of row

• the leftmost nonzero entry

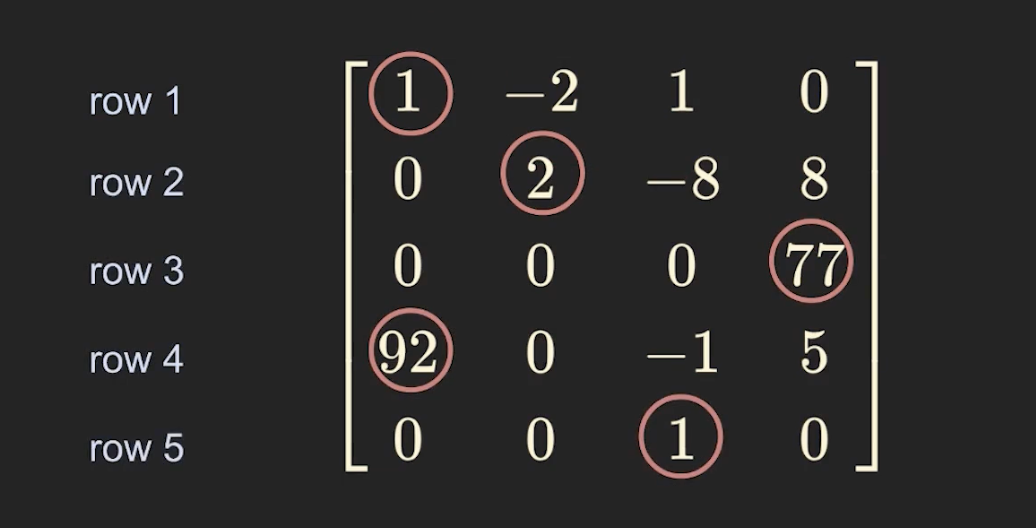
Echelon form

1. All nonzero rows are above any rows all zeros
2. Each leading entry of row is in a column to the right of the leading entry of the row above it

-> all zero인 행들이 밑단에 깔려있다 & leading entry의 순서가 아래로 갈수록 오른쪽에 있어야함(그 바로 위의 놈보다)

Reduced Echelon form

3. The leading entry in each nonzero row is 1.
4. Each leading 1 is the only nonzero entry in its column

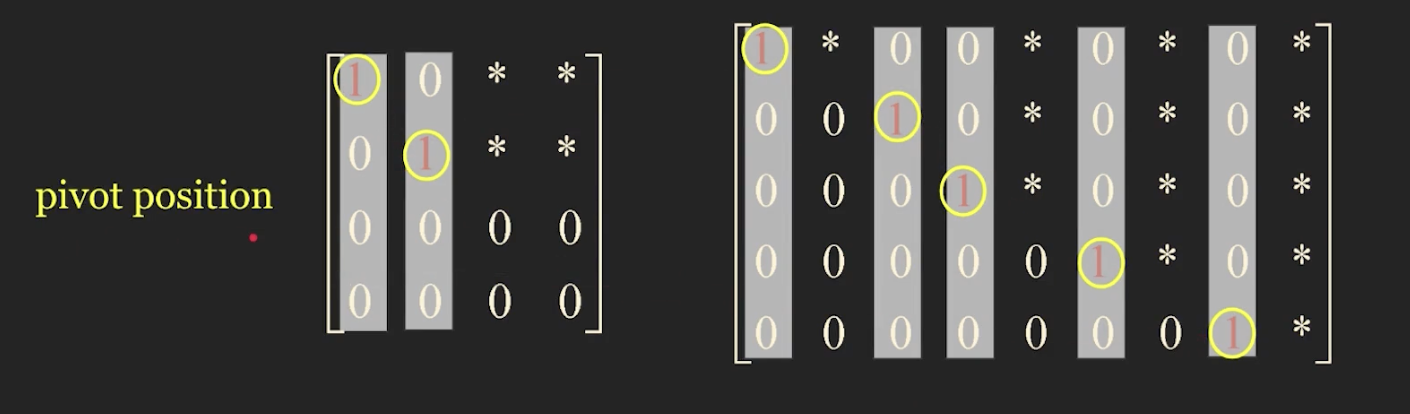
• RREF(축소된 행 계단 형태)의 정의:

1. 피벗(pivot) 위치: 행렬에서 각 행의 첫 번째 비제로 원소는 "피벗"이라고 불린다.
2. 피벗 위와 아래: 각 피벗의 위와 아래에 있는 원소는 모두 0이다.
3. 피벗 값은 1: 각 피벗은 1이어야 한다.
4. 각 피벗은 이전 행의 피벗보다 오른쪽에 있어야 한다.

Therem 1.Uniquenss of the Reduced Echelon Form
-> Each matrix is row equivalent to one and only one reduced echelon matrix.

Uniqueness of the Reduced Row Echelon Form ( 유일성 정리 )

두 행렬이 행 연산을 통해 동일한 형태로 변형될 수 있다면 그 RREF는 하나뿐이다.

• 예시로 두 행렬의 RREF를 구해보자
  

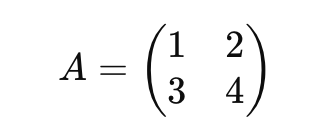
1. 첫 번째 행은 이미 피벗이 1로 설정되어 있으므로, 변경할 필요가 없다.
2. 두 번째 행에서 첫 번째 행의 3배를 빼서 0으로 만든다. -> R2 -> R2 - 3R1:
   
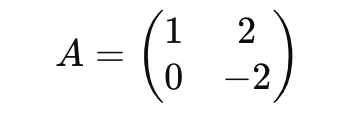
3. 이제 두 번째 행의 피벗을 1로 만들기 위해, 두 번째 행에 -1/2를 곱한다 -> R2 -> -1/2R2:
   
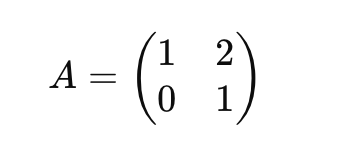
4. 마지막으로, 첫 번째 행에서 두 번째 행의 2배를 빼서 두 번째 열을 0으로 만든다.
   

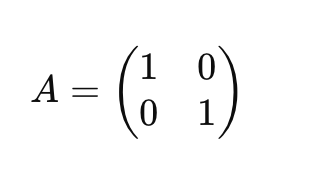
행렬 A의 RREF는 위와 같다.

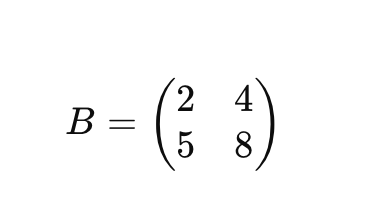
1. 첫 번째 행에서 피벗을 1로 만들기 위해, 첫 번째 행을 1/2로 나눈다 -> R1 -> 1/2R1:

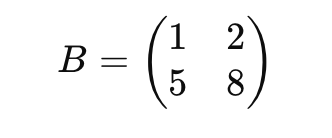
2. 두 번째 행에서 첫 번째 행의 5배를 빼서 첫 번째 열을 0으로 만든다 -> R2 -> R2 - 5R1:

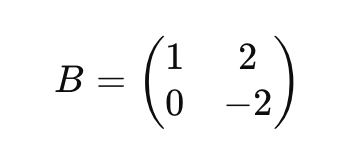
3. 두번째 행의 피벗을 1로 만들기 위해 두번째 행을 -1/2로 곱한다. -> R2 -> -1/2R2:

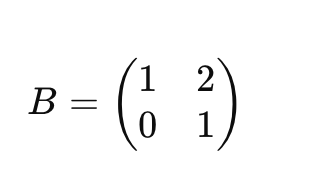
4. 첫번째 행에서 두번째 행의 2배를 뺴서 두번째 열을 0으로 만듬 -> R1 -> R1-2R2:

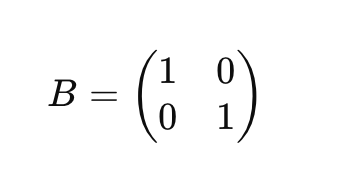
따라서 두 행렬의 RREF가 동일한 것을 볼 수 있다.

Row reduction Algorithm

1. begin with the leftmost nonzero column
   
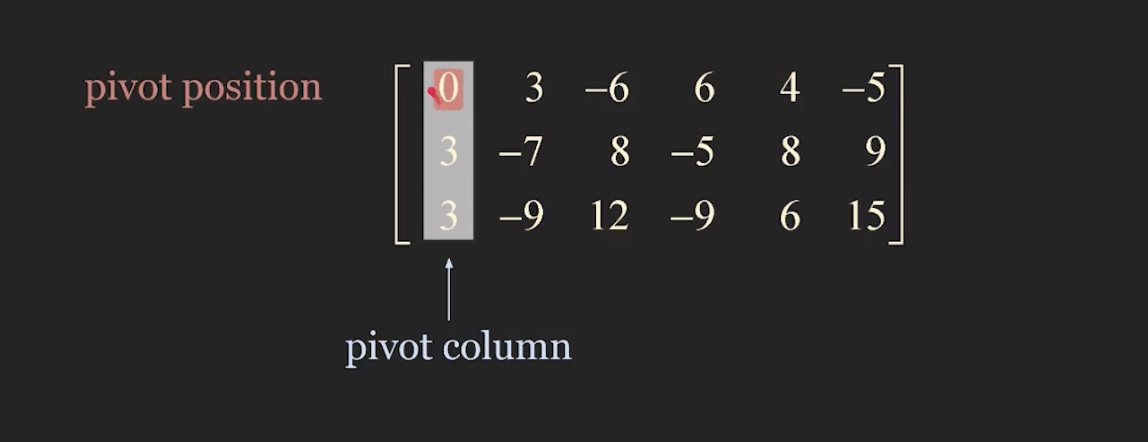
2. select a nonzero entry in the pivot column as a pivot. if necessary interchange rows to move this entry into the pivot position
   
3. row Replacement to create zeros in all positions below the pivot
   
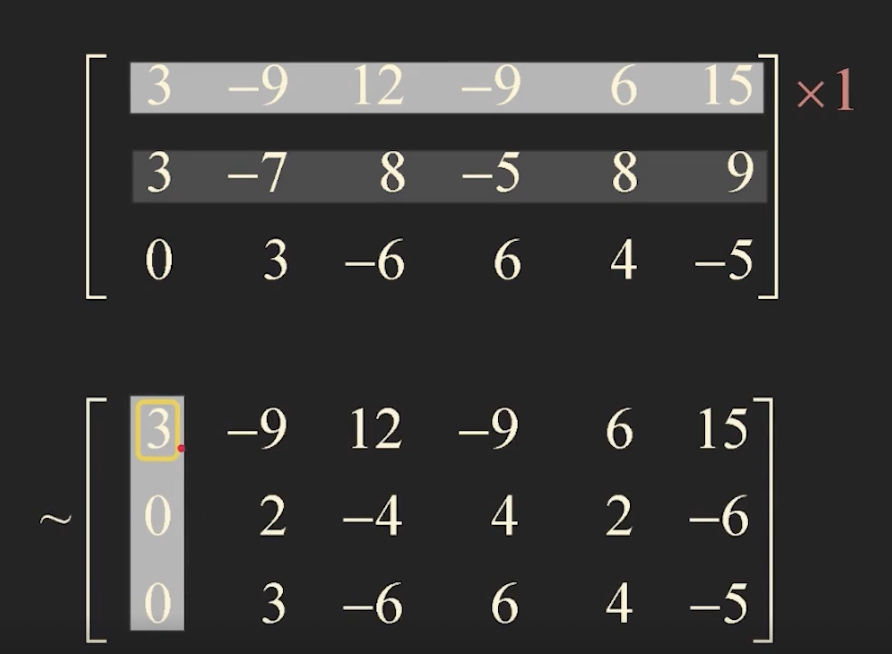
4. apply steps 1-3 to the submatrix that remain ..

-> the combination of steps 1-4 is called forward phase

--> echelon form!!

5. beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. if a pivot is not 1. make it by a scaling operation(위와 반대 방향)

step 5 is called backward phase
-> reduced echelon form!!

-> 위와 같이 x3가 free일떄 약속된 solution을 general solution이라 한다.

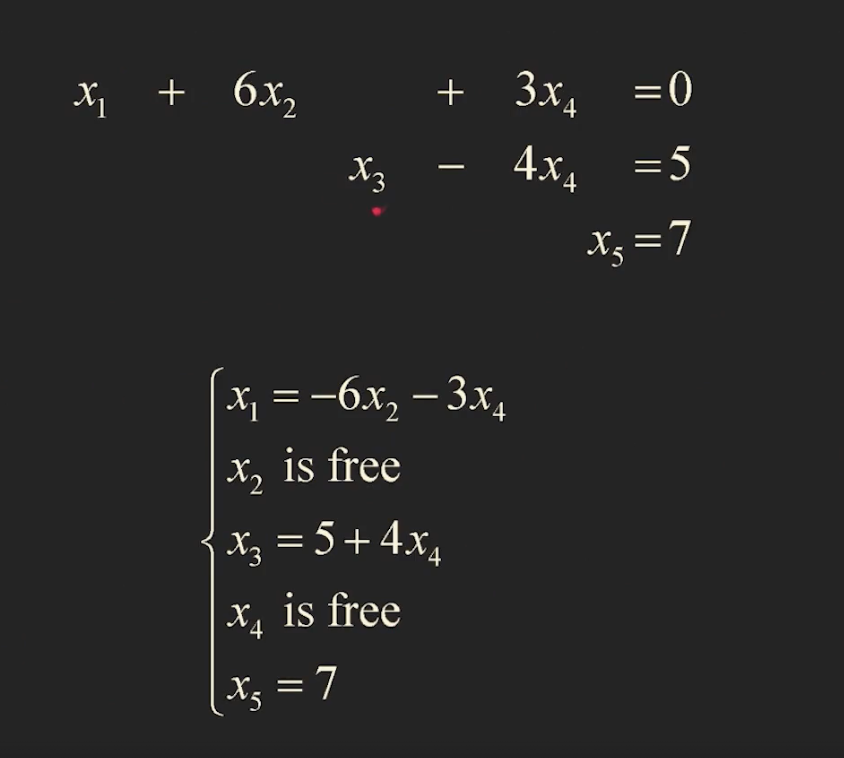
-> 이 경우일 땐??

여기서 나오는 이론이 Existence and Uniqueness Theorem이다.

[ 0 0 0 ... 0 b] with b is nonzero
-> 이런 행이 없어야 행이 있다

• 선형 시스템이 일관성이 있다면, 해는 유일하거나 무수히 많다.
• 유일한 해를 갖기 위해서는 자유변수(free variables)가 없다는 조건이 필요하다.
• 무수히 많은 해를 갖기 위해서는 자유변수가 적어도 하나 있어야 하다