인공신경망의 기본 구조
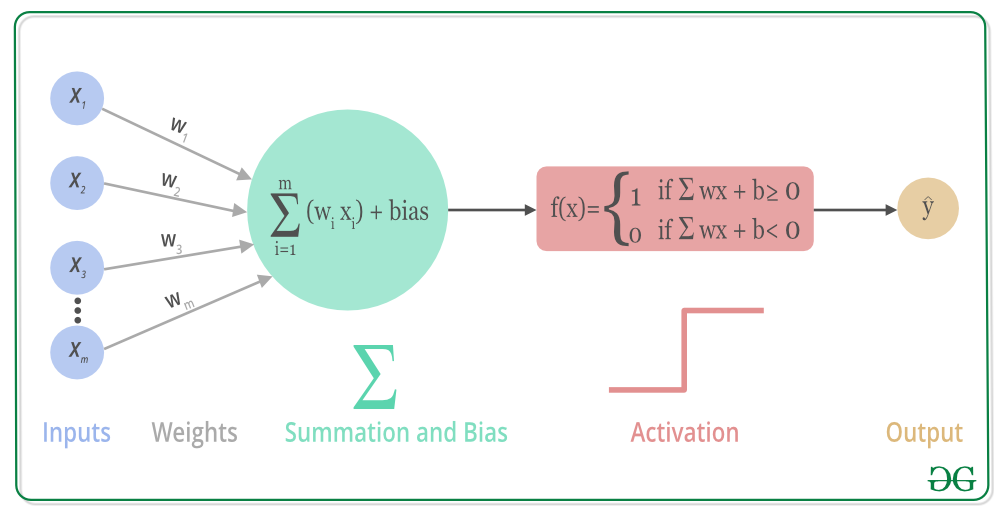
Image by Understanding Activation Functions in Depth
- 입력: 입력은 우리가 출력 값을 예측하기 위해 사용하는 값의 집합
-
가중치: 가중치는 각 입력/특징에 연결된 실수 값이며, 해당 특징이 최종 출력을 예측하는 데 중요성을 전달
-
편향: 편향은 활성화 함수를 좌우로 이동시키는 데 사용, 직선 방정식에서 y-절편과 비교할 수 있다.
-
합산 함수: 합산 함수의 역할은 가중치와 입력을 결합하여 그들의 합계를 계산
-
활성화 함수: 모델에 비선형성을 도입하는 데 사용
📌 딥러닝 코드로 구현하기
Input
X = np.array([
[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]
])sigmoid
입력값을 0과 1 사이의 값으로 압축시키는 함수
주로 이진 분류 문제에서 활성화 함수로 사용되거나, 로지스틱 회귀(Logistic Regression)와 같은 알고리즘에서 확률값을 예측하는 데에 이용
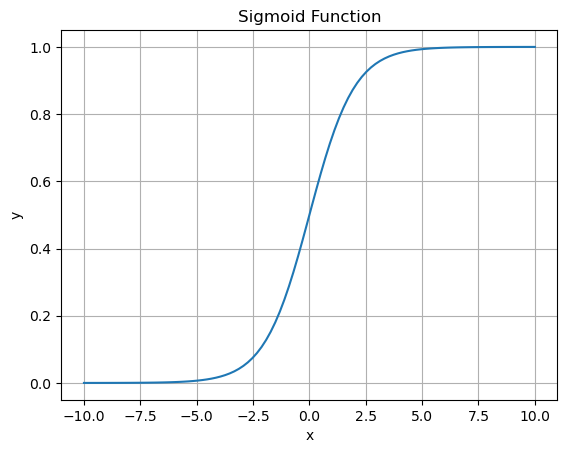
def sigmoid(x):
return 1.0/(1.0 +np.exp(-x))가중치 선택
# 가중치 랜덤하게 선택
W = 2*np.random.random((1,3))-2
W순방향 연산
N = 4
for k in range(N):
x = X[k, :].T
v = np.matmul(W, x)
y = sigmoid(v)
print(y)[0.24759829]
[0.10033613]
[0.10982636]
[0.04013482]위 연산의 가중치는 random 하게 뽑은 것이므로 y 값은 아무 의미가 없다.
가중치가 정답을 맞추도록 학습하는 과정이 필요하다.
Deep Learning Workflow

Image by Deep Learning Workflow
📌 지도학습
타겟 변수 D
D = np.array([
[0], [0], [1], [1]
])output 계산 함수
def calc_output(W, x):
v = np.matmul(W, x)
y = sigmoid(v)
return y오차 계산 함수
def calc_error(d, y):
e = d - y # 오차 계산
delta = y * (1-y) *e # error 와 활성화 함수의 미분값
return deltaGradient Descent
미분의 개념을 최적화 문제에 적용한 대표적 방법 중 하나로서 함수의 local minimum을 찾는 방법 중 하나이다.
이와 같이 어떤 함수의 극대점을 찾기 위해 현재 위치에서의 gradient 방향으로 이동해 가는 방법을 gradient ascent 방법, 극소점을 찾기 위해 gradient 반대 방향으로 이동해 가는 방법을 gradient descent 방법이라 부릅니다
기울기의 값이 크다는 것은 가파르다는 것을 의미하기도 하지만, 또 한편으로는 의 위치가 최소값/최댓값에 해당되는 좌표로부터 멀리 떨어져있는 것을 의미하기도 한다.
특정 포인트 에서 가 커질 수록 함수값이 커지는 중이라면 (즉, 기울기의 부호는 양수) 음의 방향으로
를 옮겨야 할 것이고, 반대로 특정 포인트 에서 가 커질 수록 함수값이 작아지는 중이라면 (즉, 기울기의 부호는 음수) 양의 방향으로 를 옮기면 된다.
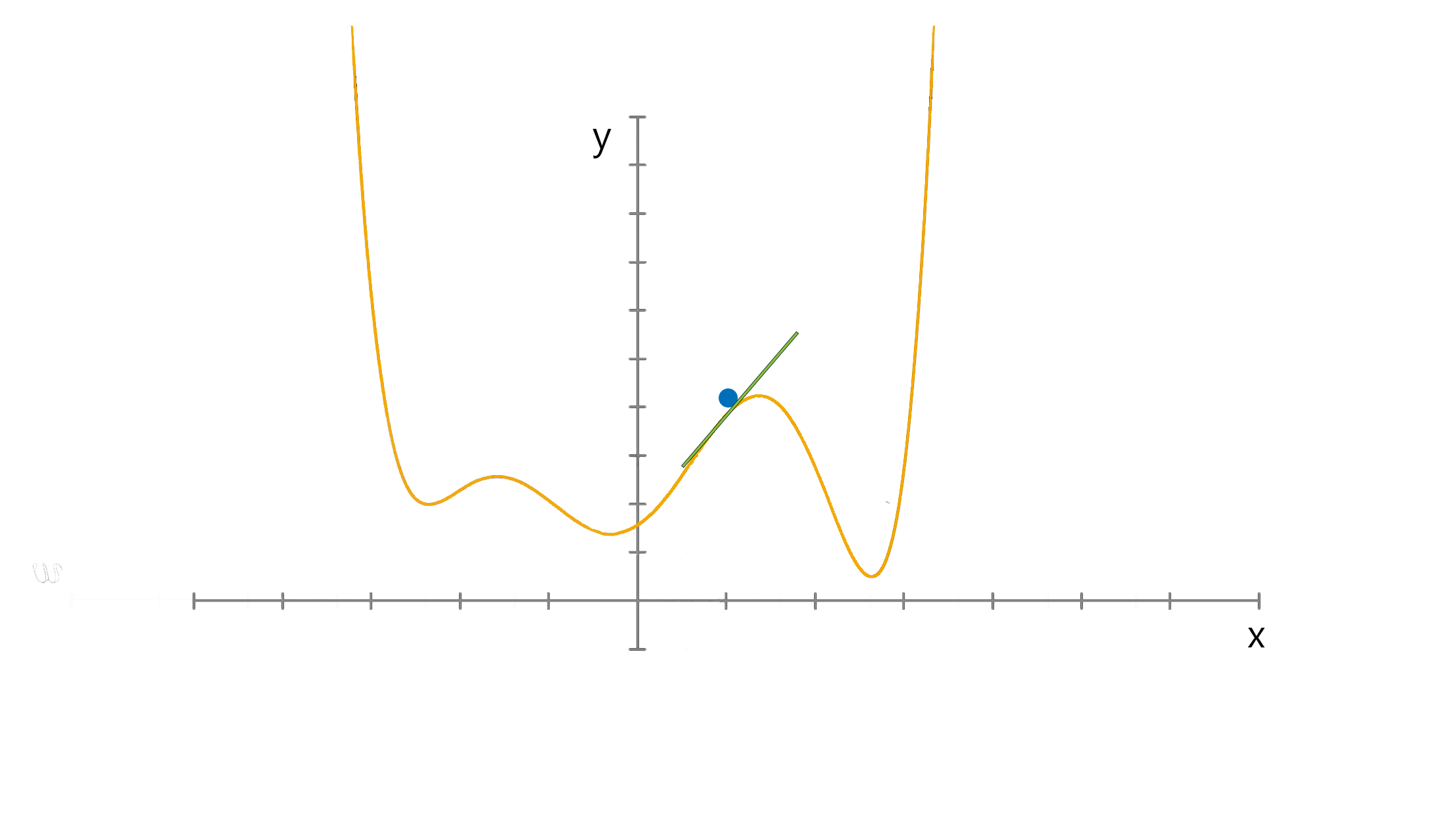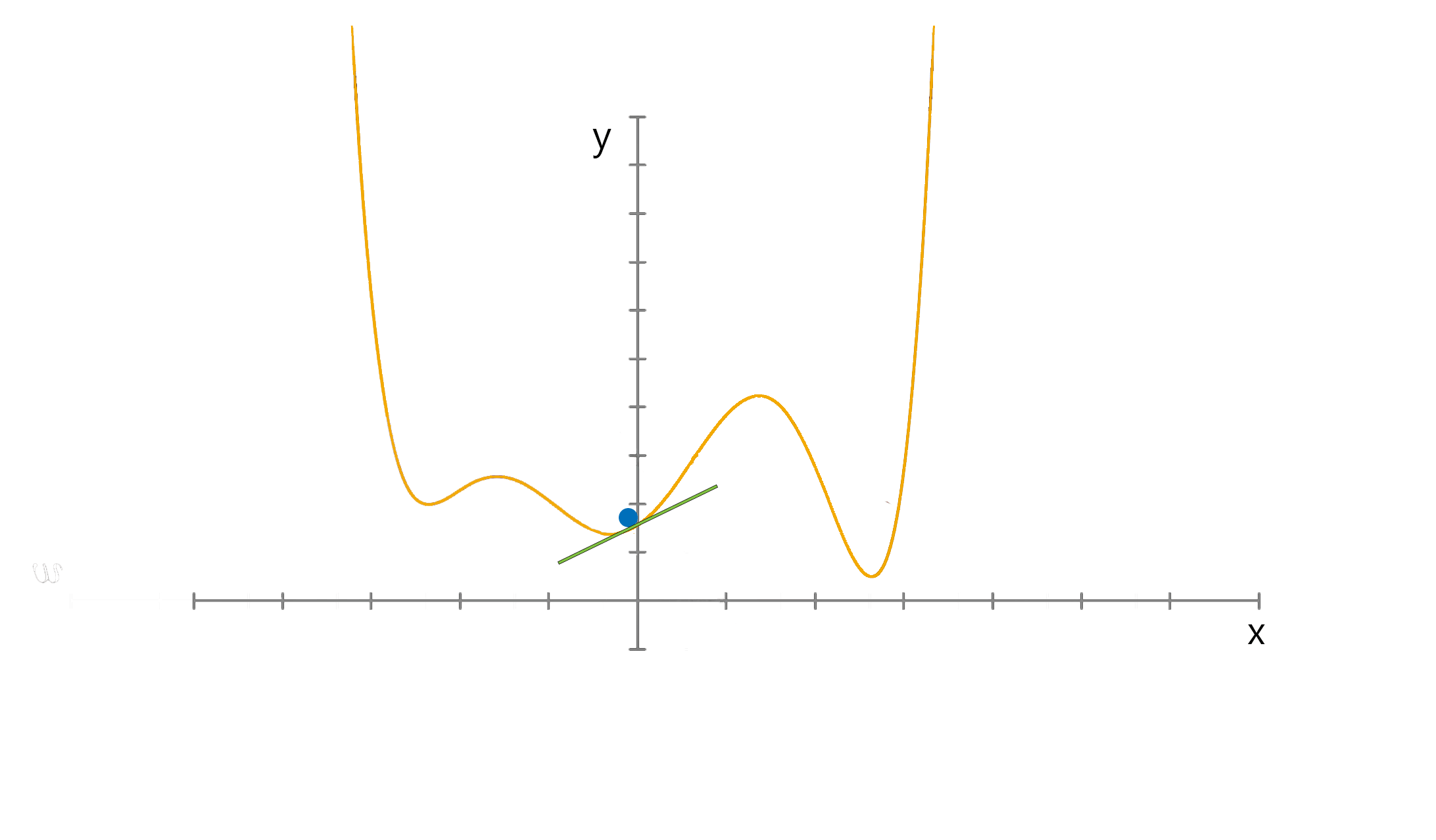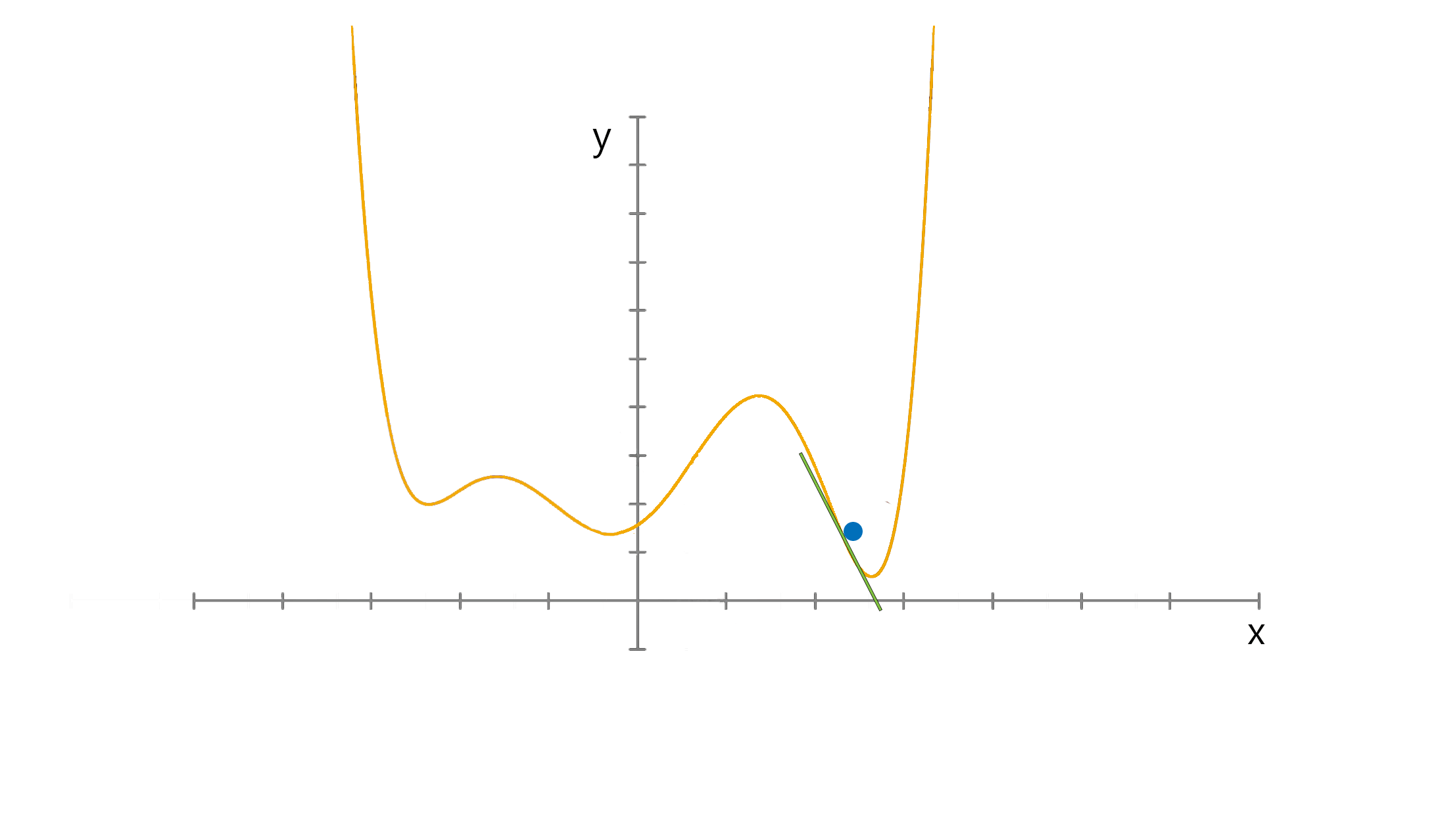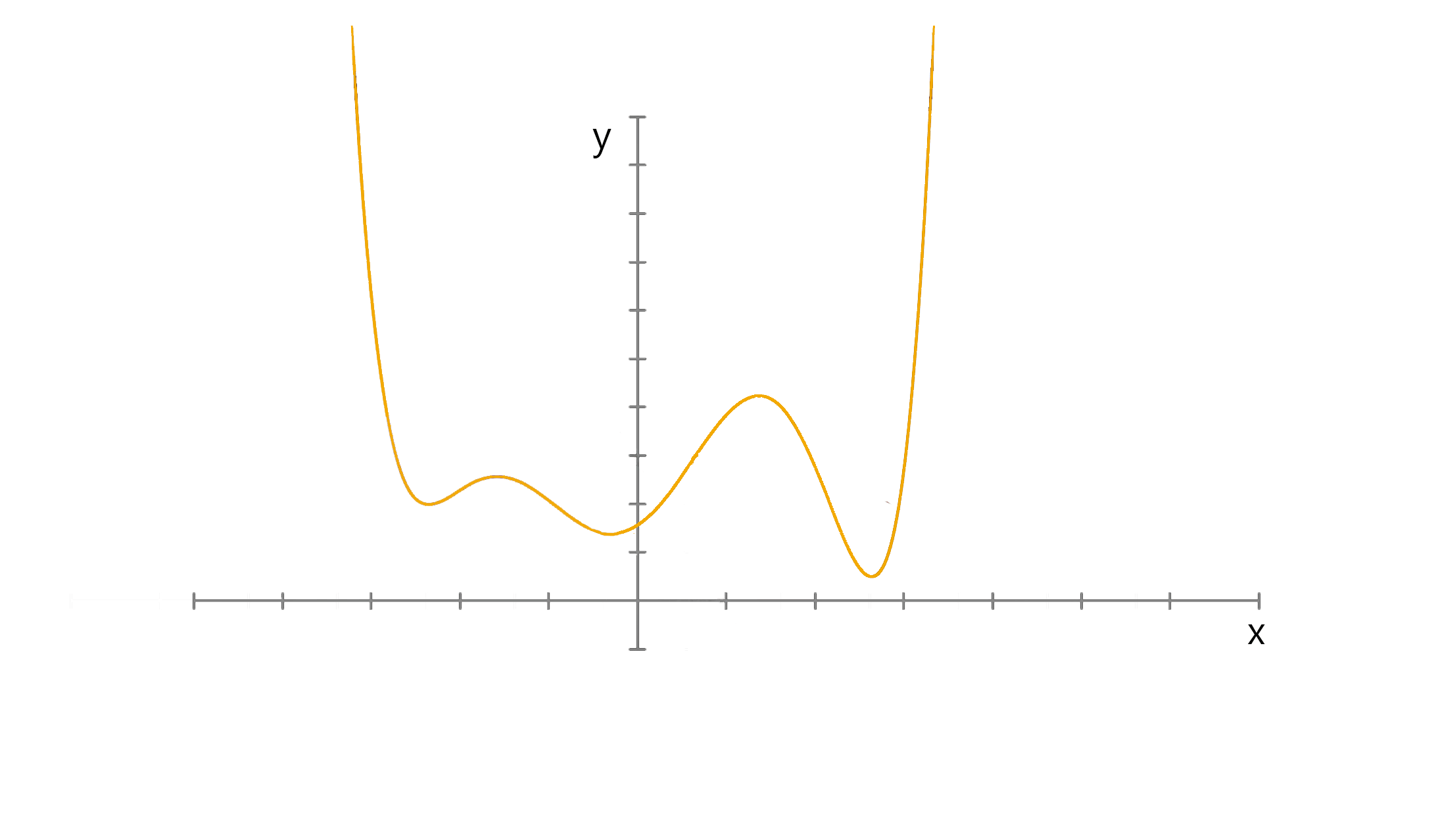
한 epoch에 수행되는 W 계산

Image by Introduction to Artificial Neural Networks part two
Image by 딥러닝(Deep learning) 살펴보기 2탄
def delta_GD(W, X, D, step_size): # step_size : Learning rate
for k in range(len(X)):
x = X[k,:].T
d = D[k]
y = calc_output(W, x)
delta = calc_error(d, y)
dW = step_size*delta*x
W = W+dW
return W
가중치 계산
가중치 랜덤하게 초기화 후 계산
W = 2*np.random.random((1,3))-1
Wstep_size = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, step_size)
print(W)
...
[[ 9.57047151 -0.19870718 -4.58366338]]
[[ 9.57057353 -0.19870784 -4.58371406]]
[[ 9.57067555 -0.19870851 -4.58376474]]
[[ 9.57077755 -0.19870917 -4.58381541]]
[[ 9.57087954 -0.19870984 -4.58386608]]
[[ 9.57098152 -0.1987105 -4.58391674]]
[[ 9.57108349 -0.19871117 -4.5839674 ]]
[[ 9.57118546 -0.19871184 -4.58401805]]
[[ 9.57128741 -0.1987125 -4.5840687 ]]
[[ 9.57138935 -0.19871317 -4.58411934]]
[[ 9.57149128 -0.19871383 -4.58416997]]
[[ 9.5715932 -0.19871449 -4.58422061]]
[[ 9.57169511 -0.19871516 -4.58427123]]
[[ 9.57179701 -0.19871582 -4.58432186]]
[[ 9.5718989 -0.19871649 -4.58437247]]결과 계산
for k in range(4):
x = X[k, :].T
v = np.matmul(W, x)
y = sigmoid(v)
print(y)정확도가 높은 결과가 출력 됐다.
[0.01010696]
[0.00830063]
[0.99322371]
[0.99174633]
📌 XOR Problem- 오차의 역전파
퍼셉트론은 초기에는 단층 구조로 제안되었으며 비선형문제에 한계를 가지고 있었고 XOR 문제는 퍼셉트론이 잘 해결하지 못하는 비선형 분류 문제 중 하나로 알려져 있다.
XOR은 배타적 논리합을 의미하며, 두 개의 입력이 다를 때 1을 출력하고, 같을 때 0을 출력하는 논리 연산을 말한다.
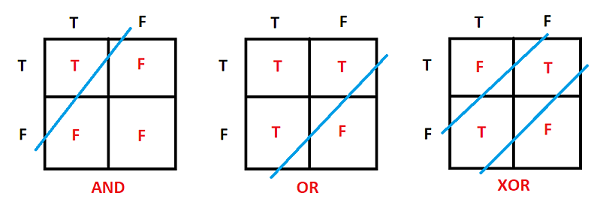
Image by Neural Network Multilayer Perceptron
XOR 데이터 설정
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,0]])
D = np.array([[0], [1], [1], [0]])
W = 2*np.random.random((1, 3))-1 가중치 학습
step_size = 0.9
for epoch in range(10000):
W = delta_GD(W, X, D, step_size)
print(W)결과 확인
for k in range(4):
x = X[k, :].T
v = np.matmul(W, x)
y = sigmoid(v)
print(y)이전 계산과 달리 정확도가 엉망이다.
[0.80224023]
[0.72165011]
[0.71000066]
[0.27834989]MLP 형태로 함수 생성
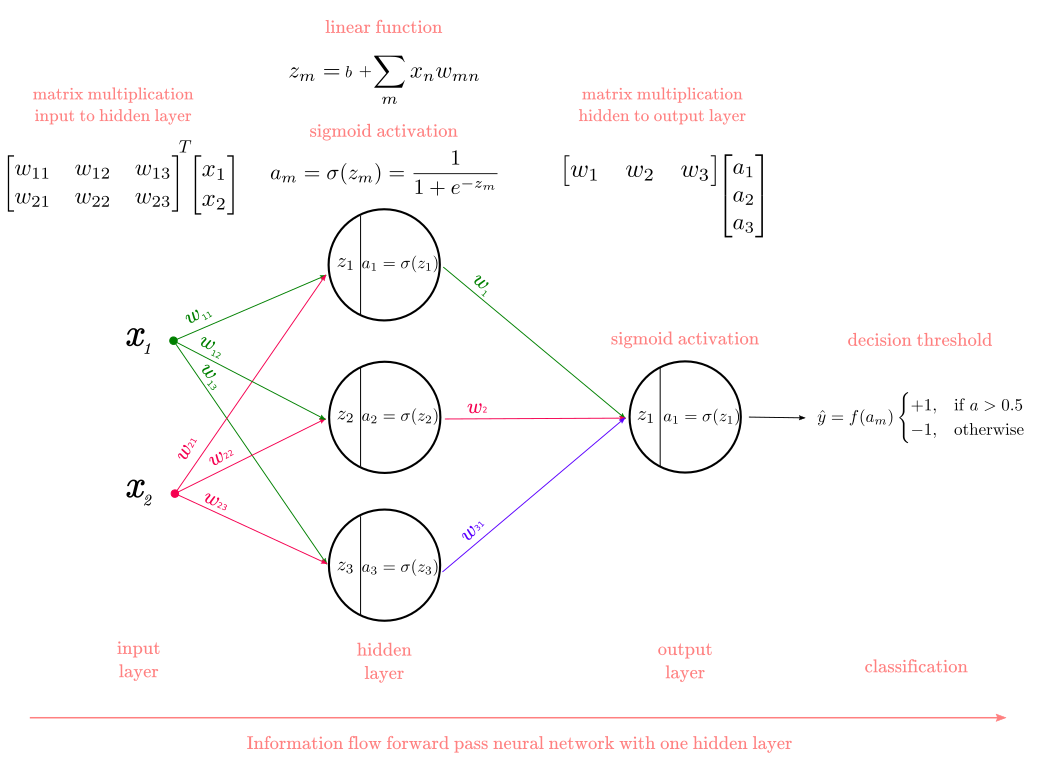
Image by The Multilayer Perceptron - Theory and Implementation of the Backpropagation Algorithm
def calc_output(W1, W2, x):
v1 = np.matmul(W1, x)
y1 = sigmoid(v1)
v = np.matmul(W2, y1)
y = sigmoid(v)
return y, y1Backpropagation
다층 퍼셉트론은 데이터가 입력되는 입력층, 결과 값을 출력하는 출력층 사이에도 여러 은닉층이 존재한다.
이들 층에 속하는 노드의 출력값은 오차를 측정할 기준이 없기 때문에 가중치를 어떻게 조정해야 하는지 알 수 없다.
오류 역전파 알고리즘은 출력층에서 발생한 오차를 출력층에서 입력층의 방향으로 보내면서, 은닉층의 노드 사이의 가중치를 재조정한다. 오류 역전파 알고리즘을 사용하면 수많은 노드층이 쌓인 다층 퍼셉트론도 학습시킬 수 있을 것으로 기대됐다

Image by Gradient Descent vs. Backpropagation: What’s the Difference?
출력층의 델타 계산 함수
def calc_delta(d, y):
e = d - y # 오차 계산
delta = y * (1-y) *e # error 와 활섬화 함수의 미분값
return delta은닉층의 델타 계산 함수
def calc_delta1(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1 * (1-y1) *e1 # error 와 활섬화 함수의 미분값
return delta1역전파 코드
def backprop_XOR(W1, W2, X, D, step_size):
for k in range(len(X)):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calc_delta(d, y)
delta1 = calc_delta1(W2, delta, y1)
dW1 = (step_size*delta1).reshape(4, 1) * x.reshape(1,3)
W1 = W1 + dW1
dW2 = step_size*delta * y1
W2 = W2+dW2
return W1, W2가중치 초기화
W1 = 2*np.random.random((4,3))-1
W2 = 2*np.random.random((1,4))-1 W1
[[ 0.69938053 -0.18997088 0.60362363]
[-0.36514783 -0.48306764 -0.63310793]
[ 0.77527251 -0.68425237 0.67617208]
[-0.63686742 0.96816049 -0.89227272]]
W2
[[ 0.50066821 0.1468759 -0.22109587 -0.20663386]]가중치를 재조정
step_size = 0.9
for epoch in range(10000):
W1, W2 = backprop_XOR(W1, W2, X, D, step_size)
print(W1)
print(W2)결과 확인
for k in range(len(X)):
x = X[k, :].T
print(calc_output(W1, W2, x)[0])정확도 높은 결과 확인
[0.01100377]
[0.99038458]
[0.9898667]
[0.00677503]📌 Cross-Entropy
엔트로피는 불확실성(uncertainty)과도 같은 개념이다. 예측이 어려울수록 정보의 양은 더 많아지고 엔트로피는 더 커진다.
크로스엔트로피는 '정답'과 예측한 '확률값' 사이에서 얼마나 차이가 발생하는지(얼마나 정보가 발생되는지)를 계산한다.
예측된 확률값들이 정답을 완벽하게 맞췄다면 크로스 엔트로피는 0이 되어 오차도 0이 된다.
예측된 확률값들이 완전히 틀리게 되면 크로스 엔트로피는 무한대로 커진다.
입력층에서 delte 계산 함수
델타를 구할 때 크로스 엔트로피를 사용하면 델타는 오차와 같다.
def calc_delta_ce(d, y):
e = d - y
delta = e
return delta은닉층에서 delte 계산 함수
def calc_delta1_ce(W2, delta, y1):
e1 = np.matmul(W2.T, delta)
delta1 = y1*(1-y1)*e1
return delta1역전파
def backprop_ce(W1, W2, X, D, step_size):
for k in range(len(X)):
x = X[k, :].T
d = D[k]
y, y1 = calc_output(W1, W2, x)
delta = calc_delta_ce(d, y)
delta1 = calc_delta1_ce(W2, delta, y1)
dW1 = (step_size*delta1).reshape(4,1) * x.reshape(1,3)
W1 = W1 + dW1
dW2 = step_size*delta*y1
W2 = W2 + dW2
return W1, W2가중치 재조정
W1 = 2*np.random.random((4,3))-1
W2 = 2*np.random.random((1,4))-1step_size = 0.9
for epoch in range(10000):
W1, W2 = backprop_ce(W1, W2, X, D, step_size)
print(W)
결과 확인
손실함수로 cross entropy를 사용하는 성능이 훨씬 좋아졌다.
[0.00010441]
[0.99982668]
[0.99982279]
[0.00022226]
📌 SoftMax Function
SoftMax Function
이진 분류문제가 아닌, 다중 분류를 해결하기 위한 모델을 제안한 것이 바로 소프트맥스 함수이다.
소프트맥스 함수는 여러 개의 연산 결과를 정규화하여 모든 클래스의 확률값의 합을 1로 만들자는 간단한 아이디어다.
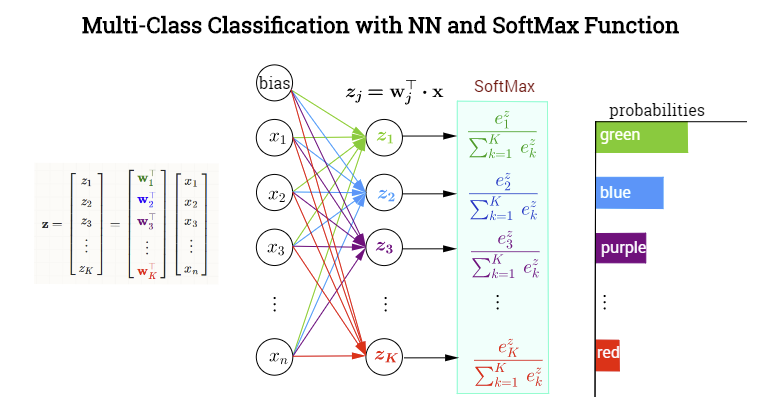
Image by Softmax Activation
soft-max
def soft_max(x):
x = np.subtract(x, np.max(x))
ex = np.exp(x) # 지수를 이용해 0 이나 음수값도 양수로 바꿔 줌
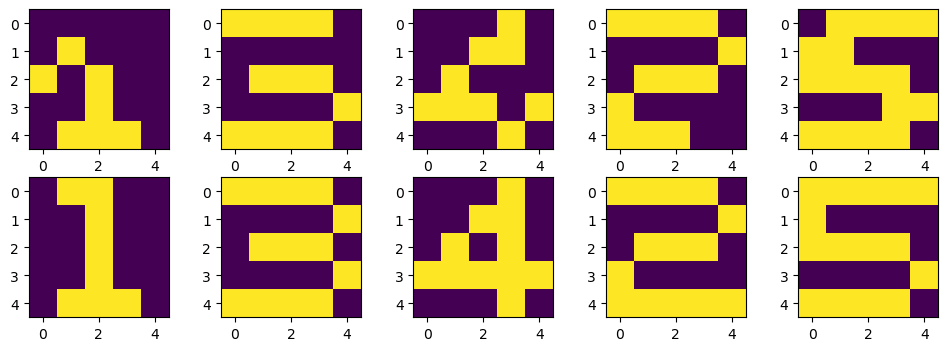
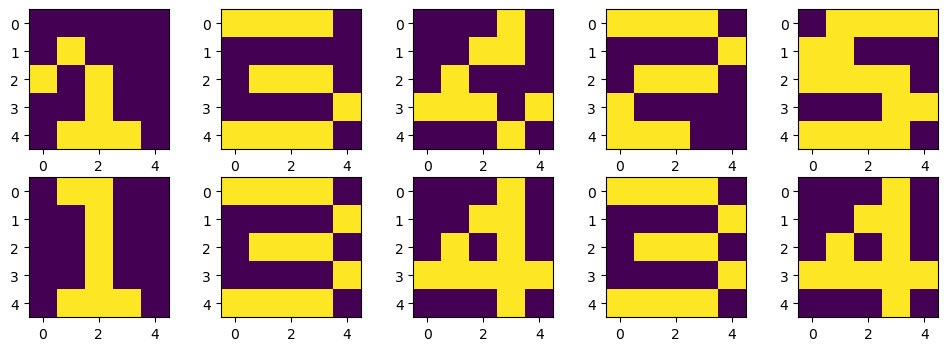
return ex/np.sum(ex)train data
X = np.zeros((5, 5, 5))
X[:, :, 0] = [[0, 1, 1, 0, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0], [0, 0, 1, 0, 0], [0, 1, 1, 1, 0]]
X[:, :, 1] = [[1, 1, 1, 1, 0], [0, 0, 0, 0, 1], [0, 1, 1, 1, 0], [1, 0, 0, 0, 0], [1, 1, 1, 1, 1]]
X[:, :, 2] = [[1, 1, 1, 1, 0], [0, 0, 0, 0, 1], [0, 1, 1, 1, 0], [0, 0, 0, 0, 1], [1, 1, 1, 1, 0]]
X[:, :, 3] = [[0, 0, 0, 1, 0], [0, 0, 1, 1, 0], [0, 1, 0, 1, 0], [1, 1, 1, 1, 1], [0, 0, 0, 1, 0]]
X[:, :, 4] = [[1, 1, 1, 1, 1], [1, 0, 0, 0, 0], [1, 1, 1, 1, 0], [0, 0, 0, 0, 1], [1, 1, 1, 1, 0]]
D = np.array([[[1, 0, 0, 0, 0]],
[[0, 1, 0, 0, 0]],
[[0, 0, 1, 0, 0]],
[[0, 0, 0, 1, 0]],
[[0, 0, 0, 0, 1]]
])데이터 확인
plt.figure(figsize=(12, 4))
for n in range(5):
plt.subplot(1, 5, n+1)
plt.imshow(X[:, :, n])
plt.show()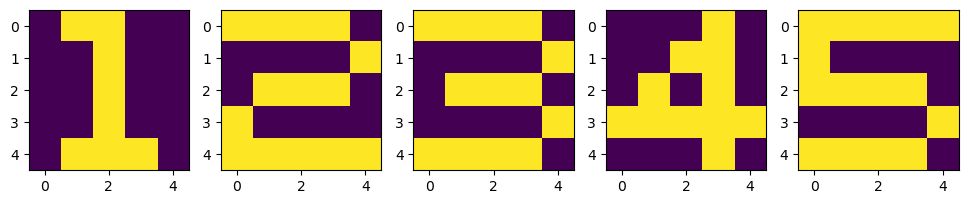
📌 ReLU 활성화 함수
ReLU 함수는 입력이 음수이면 0, 양수이면 자기 자신을 반환하여 그래디언트 소실 문제를 해결했다.
기존에는 활성 함수로 보통 시그모이드 함수를 사용했다. 시그모이드 함수는 입력이 작으면 0, 점점 커질수록 함수 값이 증가하다 일정 수준 이상에서는 다시 일정해지는 추이를 보인다. 하지만 이 경우 매우 큰 입력에 대해서도 뉴런의 결과 값은 일정하게 유지되는 한계가 있다. 반면 ReLU 함수는 매우 큰 입력에 대해서도 자기 자신을 반환하기 때문에 이러한 한계를 보정할 수 있다.
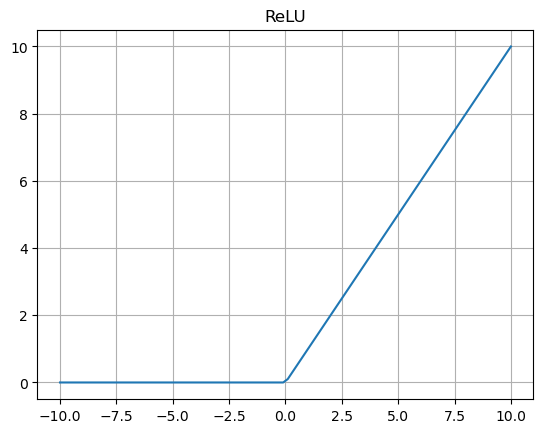
ReLU를 이용한 계산
def calcOutput_ReLU(W1, W2, W3, W4, x):
v1 = np.matmul(W1, x)
y1 = ReLU(v1)
v2 = np.matmul(W2, y1)
y2 = ReLU(v2)
v3 = np.matmul(W3, y2)
y3 = ReLU(v3)
v = np.matmul(W4, y3)
y = soft_max(v)
return y, v1, v2, v3, y1 , y2, y3
def backprop_ReLU(d, y, W2, W3, W4, v1, v2, v3):
e = d - y
delta = e # 크로스 엔트로피
e3 = np.matmul(W4.T, delta)
delta3 = (v3>0)*e3
e2 = np.matmul(W3.T, delta3)
delta2 = (v2>0)*e2
e1 = np.matmul(W2.T, delta2)
delta1 = (v1>0)*e1
return delta, delta1, delta2, delta3def calcWs(step_size, delta, delta1, delta2, delta3, y1, y2, y3, x, W1, W2, W3, W4):
dW4 = step_size * delta * y3.T
W4 = W4 + dW4
dW3 = step_size * delta3 * y2.T
W3 = W3 + dW3
dW2 = step_size * delta2 * y1.T
W2 = W2 + dW2
dW1 = step_size * delta1 * x.T
W1 = W1 + dW1
return W1, W2, W3, W4가중치 업데이트
def DeepReLU(W1, W2, W3, W4, X, D, step_size):
for k in range(len(X)):
x = np.reshape(X[:, :, k], (25, 1))
d = D[k, :].T
y, v1, v2, v3, y1, y2, y3 = calcOutput_ReLU(W1, W2, W3, W4, x)
delta, delta1, delta2, delta3 = backprop_ReLU(d, y, W2, W3, W4, v1, v2, v3)
W1, W2, W3, W4 = calcWs(step_size, delta, delta1, delta2, delta3,
y1, y2, y3, x, W1, W2, W3, W4)
return W1, W2, W3, W4 모델 학습
from tqdm.notebook import tqdm
W1 = 2*np.random.random((20, 25)) -1
W2 = 2*np.random.random((20, 20)) -1
W3 = 2*np.random.random((20, 20)) -1
W4 = 2*np.random.random((5, 20)) -1
step_size = 0.01
for epoch in tqdm(range(10000)):
W1, W2, W3, W4 = DeepReLU(W1, W2, W3, W4, X, D, step_size)
훈련 데이터 검증
def verify_algorithm(x, W1, W2, W3, W4):
v1 = np.matmul(W1, x)
y1 = ReLU(v1)
v2 = np.matmul(W2, y1)
y2 = ReLU(v2)
v3 = np.matmul(W3, y2)
y3 = ReLU(v3)
v = np.matmul(W4, y3)
y = soft_max(v)
for k in range(len(X)):
x = np.reshape(X[:, :, k], (25, 1))
y = verify_algorithm(x, W1, W2, W3, W4)
print("Y = {} :".format(k+1))
print(np.argmax(y, axis=0)+1) #가장 높은 값의 인덱스
print(y)
print('---------')훈련데이터에서는 높은 정확도를 보임
Y = 1 :
[1]
[[9.99982018e-01] # 가장 높음 : 1
[8.04877229e-09]
[3.90394720e-06]
[5.14660277e-06]
[8.92343680e-06]]
---------
Y = 2 :
[2]
[[1.86376108e-12]
[9.99991748e-01] # 가장 높음 : 2
[7.96608003e-06]
[2.37828345e-07]
[4.83868289e-08]]
---------
Y = 3 :
[3]
[[9.82986479e-06]
[2.80240721e-06]
[9.99965317e-01] # 가장 높음 : 3
[2.03174401e-05]
[1.73292520e-06]]
---------
Y = 4 :
[4]
[[1.82736967e-10]
[2.69922248e-07]
[1.08328780e-05]
[9.99983585e-01] # 가장 높음 : 4
[5.31216307e-06]]
---------
Y = 5 :
[5]
[[3.32850387e-06]
[9.83283109e-06]
[1.14494912e-05]
[1.81967418e-07]
[9.99975207e-01]] # 가장 높음 : 5
---------테스트 데이터
# 테스트 데이터
X_test = np.zeros((5, 5, 5))
X_test[:, :, 0] = [[0, 0, 0, 0, 0], [0, 1, 0, 0, 0], [1, 0, 1, 0, 0], [0, 0, 1, 0, 0], [0, 1, 1, 1, 0]]
X_test[:, :, 1] = [[1, 1, 1, 1, 0], [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 1], [1, 1, 1, 1, 0]]
X_test[:, :, 2] = [[0, 0, 0, 1, 0], [0, 0, 1, 1, 0], [0, 1, 0, 0, 0], [1, 1, 1, 0, 1], [0, 0, 0, 1, 0]]
X_test[:, :, 3] = [[1, 1, 1, 1, 0], [0, 0, 0, 0, 1], [0, 1, 1, 1, 0], [1, 0, 0, 0, 0], [1, 1, 1, 0, 0]]
X_test[:, :, 4] = [[0, 1, 1, 1, 1], [1, 1, 0, 0, 0], [1, 1, 1, 1, 0], [0, 0, 0, 1, 1], [1, 1, 1, 1, 0]]
learning_result = [0, 0, 0, 0, 0]
for k in range(len(X_test)):
x = np.reshape(X_test[:, :, k], (25, 1))
y = verify_algorithm(x, W1, W2, W3, W4)
learning_result[k] = np.argmax(y, axis=0)+1
결과 비교
학습 데이터에 과도하게 적합되어 새로운 데이터에 대한 성능이 떨어짐
1, 3, 4, 2, 5 ➡️ 1, 3, 4, 3, 4 로 예측
📌 DropOut
인공신경망에 융통성을 주기 위해서 학습 시킬 때, 일부러 정보를 누락시켜 일부에 집착하지 않고 중요한 요소가 무엇인지 파악한다.
def drop_out(y, ratio):
ym = np.zeros_like(y)
num = round(y.size*(1-ratio)) # 1 -ratio % 만큼의 데이터의 수
idx = np.random.choice(y.size, num, replace=False) # dropout 시킬 index 추출
ym[idx] = 1. / (1. - ratio)
return ym
def calcOutput_Dropout(W1, W2, W3, W4, x):
v1 = np.matmul(W1, x)
y1 = sigmoid(v1)
y1 = y1*drop_out(y1, 0.2)
v2 = np.matmul(W2, y1)
y2 = sigmoid(v2)
y2 = y1*drop_out(y2, 0.2)
v3 = np.matmul(W3, y2)
y3 = sigmoid(v3)
y3 = y3*drop_out(y3, 0.2)
v = np.matmul(W4, y3)
y = soft_max(v)
return y, v1, v2, v3, y1, y2, y3
def backprop_sigmoid(d, y, W2, W3, W4, y1, y2, y3):
e = d - y
delta = e # 크로스 엔트로피
e3 = np.matmul(W4.T, delta)
delta3 = y3*(1-y3)*e3
e2 = np.matmul(W3.T, delta3)
delta2 = y2*(1-y2)*e2
e1 = np.matmul(W2.T, delta2)
delta1 = y1*(1-y1)*e1
return delta, delta1, delta2, delta3 def DeepDropout(W1, W2, W3, W4, X, D, step_size):
for k in range(len(X)):
x = np.reshape(X[:, :, k], (25, 1))
d = D[k, :].T
y, v1, v2, v3, y1, y2, y3 = calcOutput_Dropout()(W1, W2, W3, W4, x)
delta, delta1, delta2, delta3 = backprop_sigmoid()(d, y, W2, W3, W4, y1, y2, y3)
W1, W2, W3, W4 = calcWs(step_size, delta, delta1, delta2, delta3,
y1, y2, y3, x, W1, W2, W3, W4)
return W1, W2, W3, W4 Dropout을 이용한 결과 확인
DropOut 을 통해 Overfitting 문제가 해결되어 정확도가 높아졌다