Machine Learning by professor Andrew Ng in Coursera

Classification and Representation

1) Classification

분류에도 선형 회귀를 적용할 수 있다.
0.5를 기준으로 값이 더 크면 1로 매핑, 작으면 0으로 매핑하는 것이다.
하지만 이 방법은 분류가 실제로 선형 함수가 아니기 때문에 잘 작동하지 않는다.

• 0 : 음성 클래스 (보통 찾으려는 것이 없는 경우를 말함 )

• 1 : 양성 클래스
  0, 1 외에도 0, 1, 2, ... 등으로 값을 분류하는 것은 multiclass classification

• 악성 / 양성종양 분류 작업을 위한 training set 예시

  • 우선 이미 알고있는 선형회귀 알고리즘을 데이터에 적용해 본다.
    -즉, $h_θ(x)=θ^Tx$ 직선을 그린다.
    -0.5를 임곗값으로 설정한다.
    
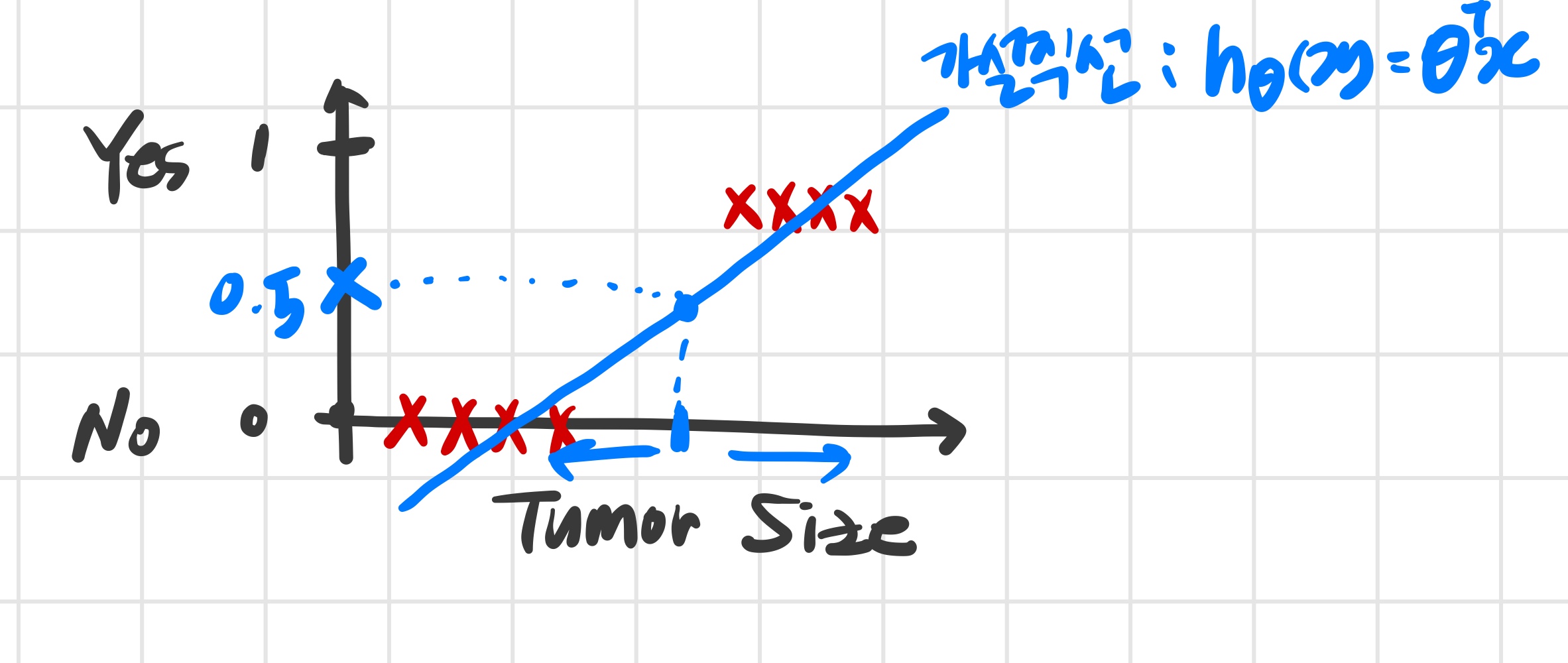
  • 새로운 데이터가 추가된다면 새로운 가설이 필요하다.
  • 새로운 직선을 그리다 보면 이전에는 양성으로 분류된 데이터가 이후에는 음성으로 분류되기도 한다.
    즉, 선형회귀를 분류문제에 적용하는 건 적절하지 않다.
    => 로지스틱 회귀를 배운다.

2) Hypothesis Representation

Logistic regression 의 hypothesis function은 $0 <= h_θ(x) <= 1$을 만족하기 위해 $h_θ(x)$을 아래와 같이 변형한다.

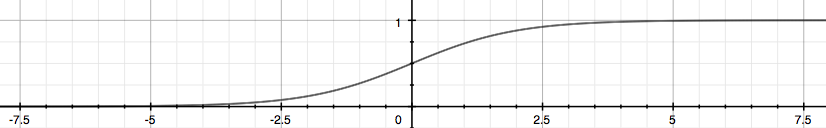
를 시그모이드 함수 또는 로지스틱 함수라고 한다.

• 주어지는 훈련샘플들로 매개변수 $θ$의 값을 정하고 이렇게 만든 가설로 새로운 입력에 대해 예측한다.

• 가설 $h_θ(x)$에 대한 해석

  • y가 1이 될 확률
    예를 들어 $h_θ(x)$ = 0.7 이라면 output이 1이 될 확률은 70%다.
    -> 따라서 0이 될 확률은 30%

3) Decision Boundary

• y값은 $h_θ(x) = g(x)$가 0.5보다 크고 작은지에 따라 결정된다.
  그런데 $h_θ(x) = g(x)$가 0.5 이상이 되는 경우는 $θ^Tx$ ≥0일 때, 0.5 이하가 되는 경우는 $θ^Tx$<0 일 때이다.

즉,

• decision boundary는 y=0 과 y=1을 구분하는 선으로 hypothesis function에 의해 결정된다.
• $θ$가 decision boundary를 결정한다.
  training set는 파라미터 $θ$를 결정하는데 사용될 뿐, decision boundary를 결정하지 않는다.