[ML] 8주차-4 : Applying PCA

Machine Learning by professor Andrew Ng in Coursera

1) Reconstruction from Compressed Representation

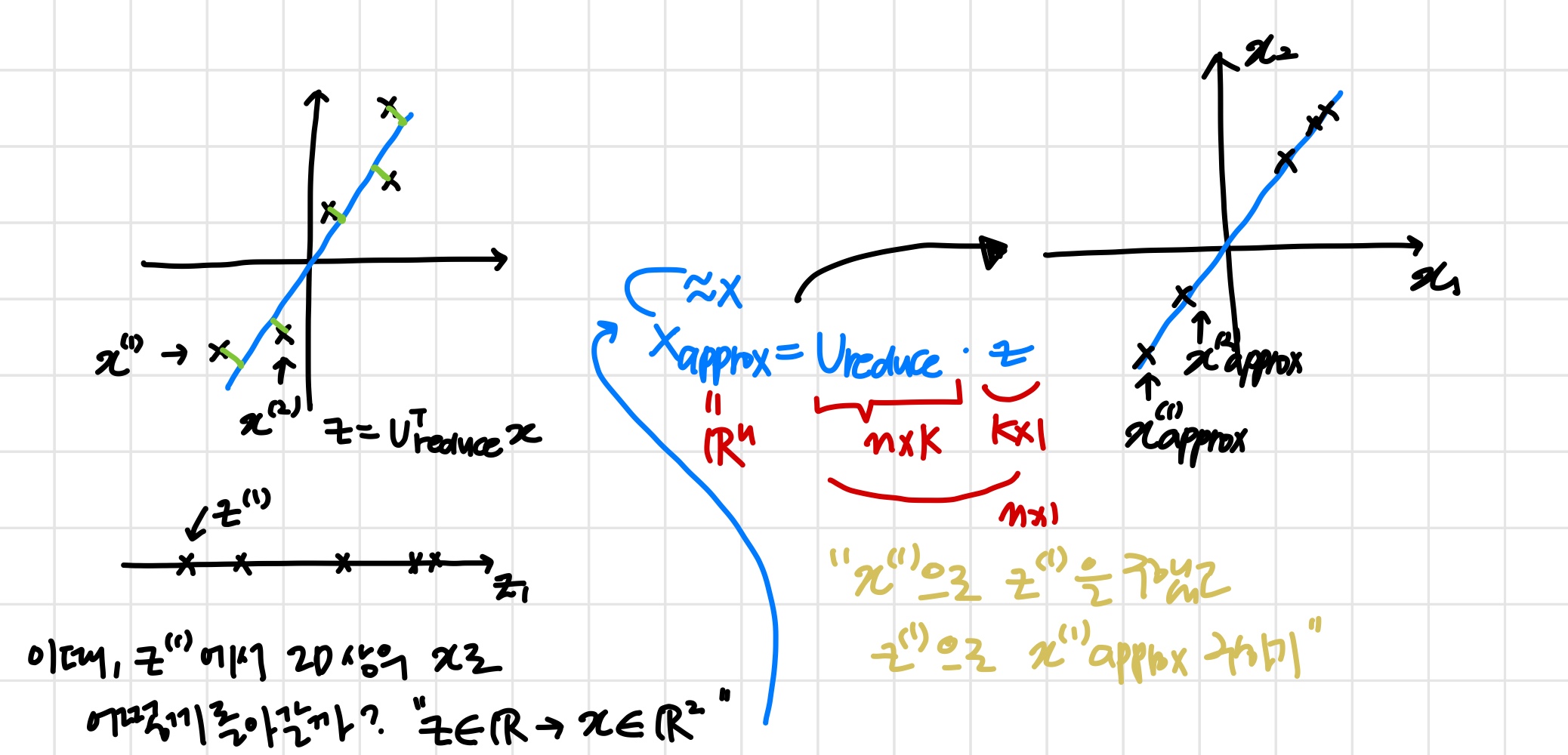
pca로 압축한 데이터에서 원래 데이터로 돌아가려고 한다.

$x_{approx}$ 즉, 근삿값을 얻을 수 있다.

2) Choosing the Number of Principal Components

'k는 pca 알고리즘의 파라미터다.'

Choosing $k$ (number of principal components)

---

• Average squared projection error :
  $\frac{1}{m}\sum_{i=1}^{m}||x^{(i)} - x_{approx}^{(i)}||^2$
  '원본 데이터와 복구한 원본 근삿값과의'
• Total variation in the data :
  $\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}||^2$
  '원점과의'

'pca가 하려는 건 위 식의 값들을 최소화하는 것'

• 아래의 식을 만족하는 $k$ 중 가장 작은 값을 선택한다.
  $\frac{ \frac{1}{m} \sum_{i=1}^{m} || x^{(i)}-x_{\text{approx}}^{(i)} ||^2 } { \frac{1}{m} \sum_{i=1}^{m}||x^{(i)}||^2 } \leq 0.01 \quad (1\%)$
  위의 식을 만족할 때, "variance의 99%가 보존되었다" 라고 한다.
  '95~99가 가장 흔하다.'

Algorithm1

• Try PCA with k=1
• Compute $U_{reduce}, z^{(1)}, z^{(2)}...,z^{(m)}, x_{approx}^{(1)}, ...x_{approx}^{(m)}$
• Check if
  $\frac{ \frac{1}{m} \sum_{i=1}^{m} || x^{(i)}-x_{\text{approx}}^{(i)} ||^2 } { \frac{1}{m} \sum_{i=1}^{m}||x^{(i)}||^2 } \leq 0.01$
  이때 조건을 만족하지 않는다면 k=2, 3, ... 로 k값을 늘려가며 위의 과정을 다시 반복한다.

이 방법은 비효율적이다.

Algorithm2
SVD(Singular Value Decomposition)를 이용한다.

이때 $S$는 "Squared matrix"

위의 식을 만족하는 가장 작은 $k$를 구한다.
이전 방법에서는 $k$ 값을 1씩 증가시키면서 조건을 만족하는지 확인했는데 SVD 함수를 한 번만 실행하면 된다.

3) Advice for Applying PCA

이전에 PCA가 알고리즘의 실행속도를 높이기 위해 쓰이기도 한다고 했었다.

Supervised learning speedup

---

예를 들어 $x^{(i)} \in R^{10,000}$ 인 경우, 연산 속도는 느릴 수 밖에 없다.
이때 PCA로 dimension을 축소할 수 있다.

• 우선 Extract inputs
  • Unlabeled dataset:
    $x^{(1)}, x^{(2)}, ...x^{(m)} \in R^{10,000}$
    PCA를 적용한다.
    $z^{(1)}, z^{(2)}, ...z^{(m)} \in R^{1000}$
• New training set:
  $(z^{(1)}, y^{(1)}), (z^{(2)}, y^{(2)}), ...(z^{(m)}, y^{(m)})$
  를 학습 알고리즘에 대입하면
  $h_\theta(z) = \frac{1}{1+e^{-\theta^Tz}}$
• 이때 만약 새로운 test data가 들어오면 똑같은 방법으로 PCA를 적용해서 $z$로 바꿔야 한다.
  $x_{test} -> z_{test}$

Note: Mapping(feature scaling, normalization, $U_{reduce}$..) should be defined by running only on the training set.
training set에서 mapping이 결정된 후, $x_{cv}^{(i)}$ 와 $x_{test}^{(i)}$에도 똑같이 적용한다.
"Run PCA only on training set not on cv or test,
$x ->z$로 가는 mapping을 정의했다면
then apply that mapping to cv set & test set"

Application of PCA

---

• Compression
  • Reduce memory/disk needed to store data
  • Speed up learning algorithm
    Choose k by ~% of variance retained
• Visualization
  k=2 or k=3
  

Bad use of PCA : To prevent overfitting

---

feature의 개수($k<n$)를 줄이기 위해 $x^{(i)}$대신 $z^{(i)}$를 사용한다.
feature 개수가 줄었기 때문에 overfit을 막을 수 있나?

$x^{(i)}$ 대신 $z^{(i)}$를 사용하면 실제로 feature개수가 줄어들긴 한다.
그러나 overfitting을 해결하는 좋은 방법은 아니다.
overfitting 해결책으로는 regularization을 쓰자.

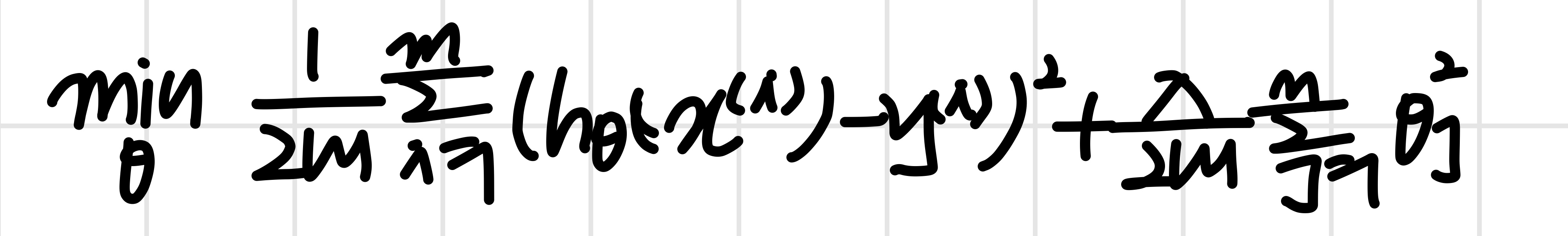
왜 regularization이 더 나은가
일단 PCA에서 $y$는 쓰이지 않는다.
PCA는 $y$ 값을 고려하지 않고 데이터의 차원을 줄이거나 어떤 정보들은 버리기도 한다.
하지만 regularization은 $y$값을 알고 있는 상태이며 따라서 PCA보다 더 나은 결과를 낸다.

PCA를 실행하기 전에, 원본데이터 $x^{(i)}$로 해보고 싶은 것들을 우선 시도한다.
만약 원하는 대로 동작하지 않는다면 그때 PCA를 실행하고 $z^{(i)}$를 고려한다.