Machine Learning by professor Andrew Ng in Coursera
Anomaly Detection
1) Problem Motivation
Anomaly detection example
내가 비행기 엔진을 제작하는 사람이라고 가정한다.
좋은 엔진을 가려내기 위해 feature들을 테스트해 보려고 한다.

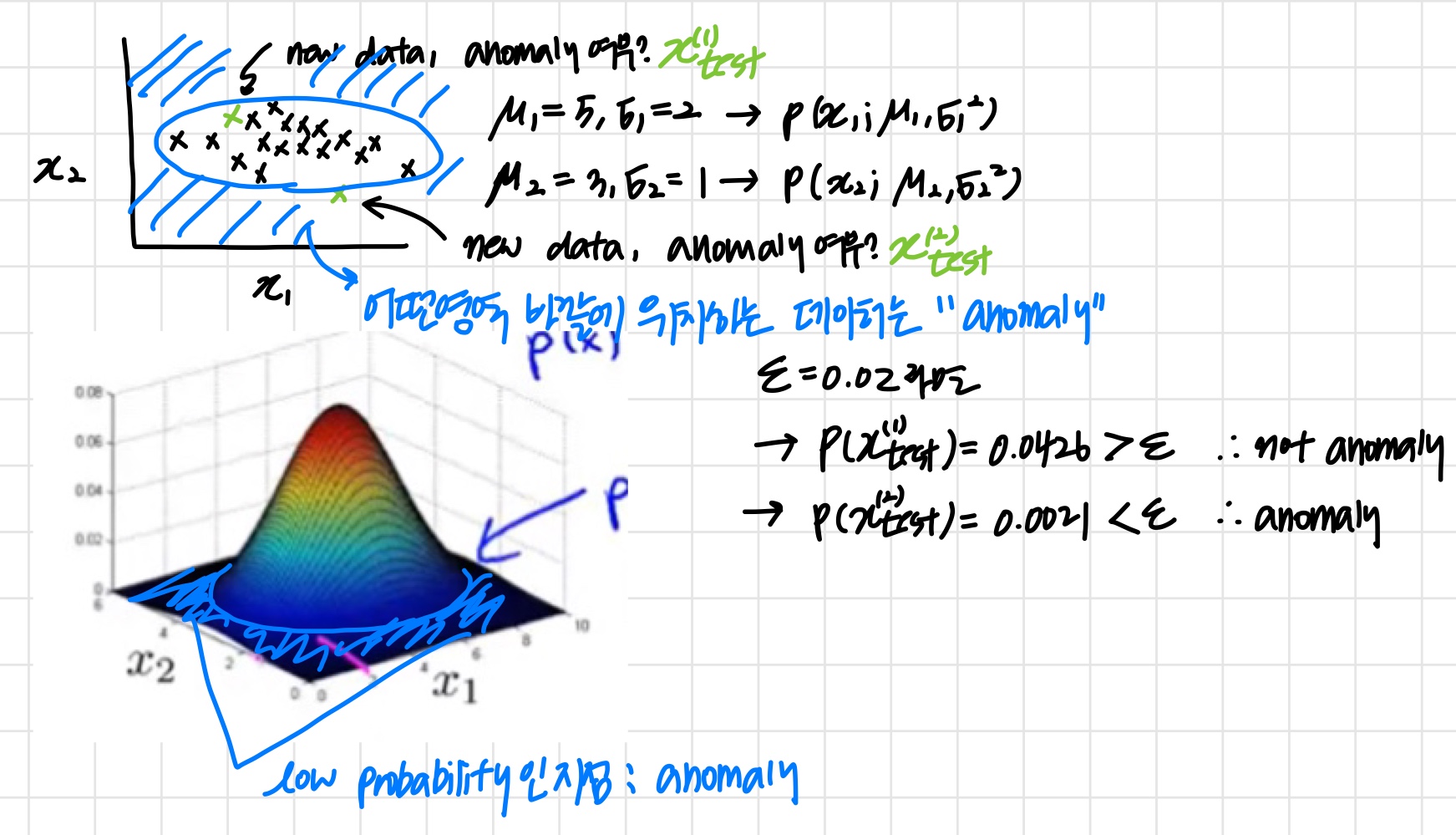
새로운 엔진을 기존의 데이터와 함께 표시하면
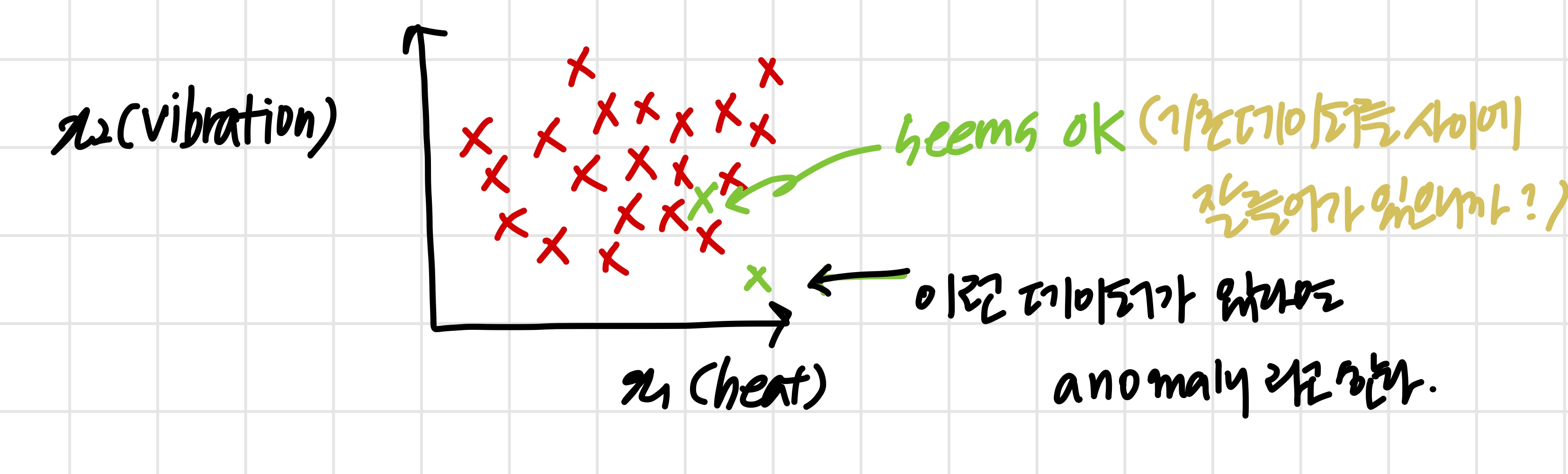
'기존 데이터와 비슷하게 잘 섞이면 괜찮다. 새로운 데이터가 튄다면 anomaly '
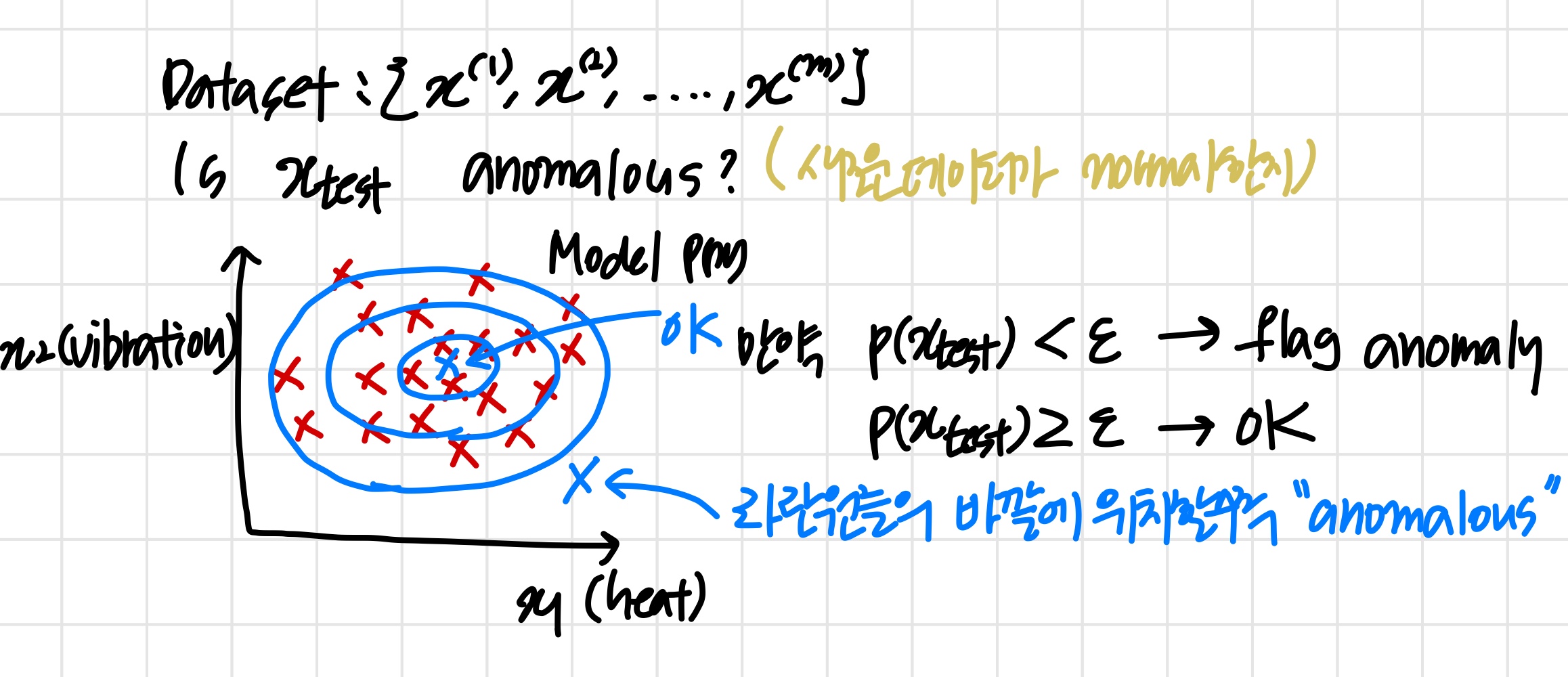
Density estimation
'새로운 데이터가 normal / anomalous 인지 판단하는 방법'
Anomaly detection example
- Fraud detection
- x(i)=features of user i’s activities
- Model p(x) from data
- p(x)<=ϵ인 이상한 유저들을 식별한다.
2) Gaussian Distribution
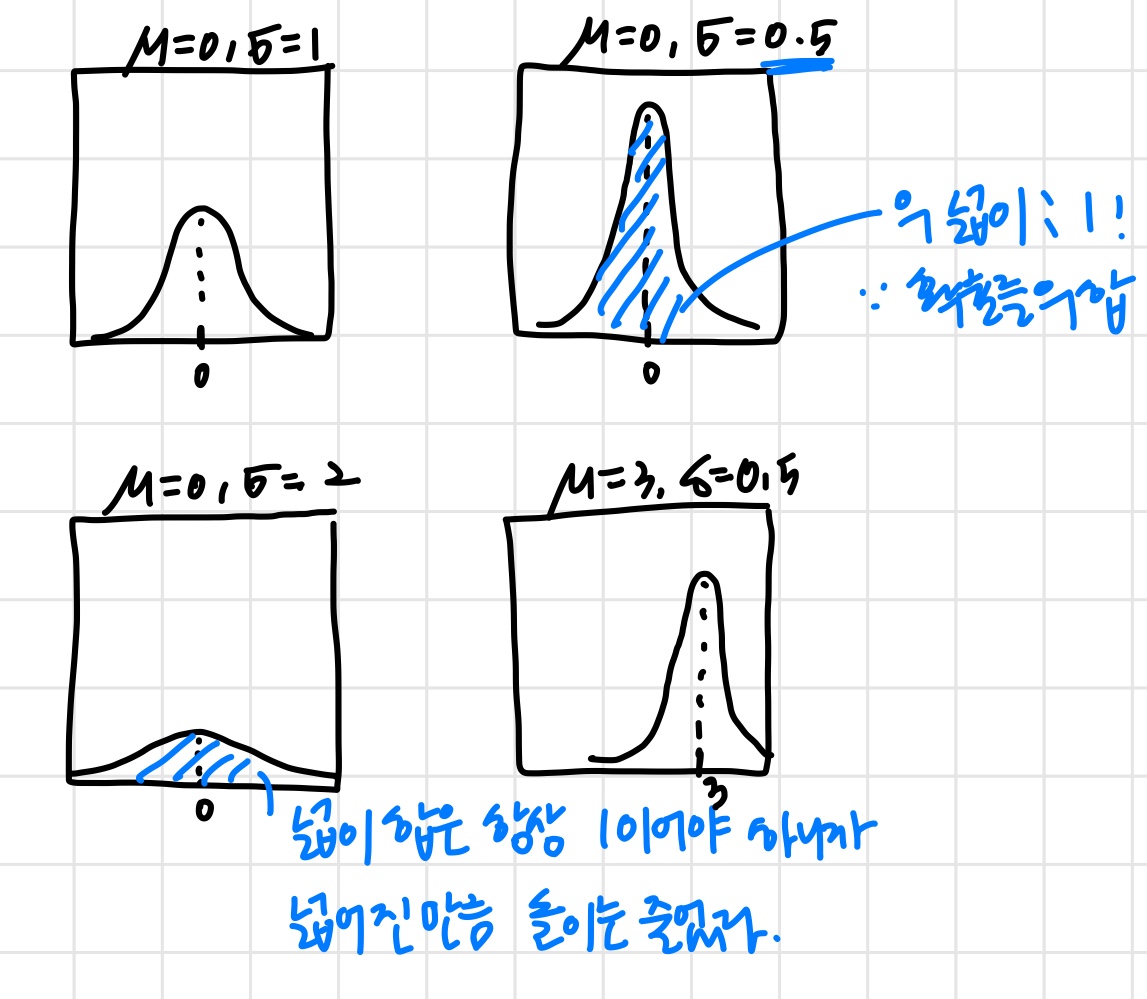
Gaussian (Normal) distribution
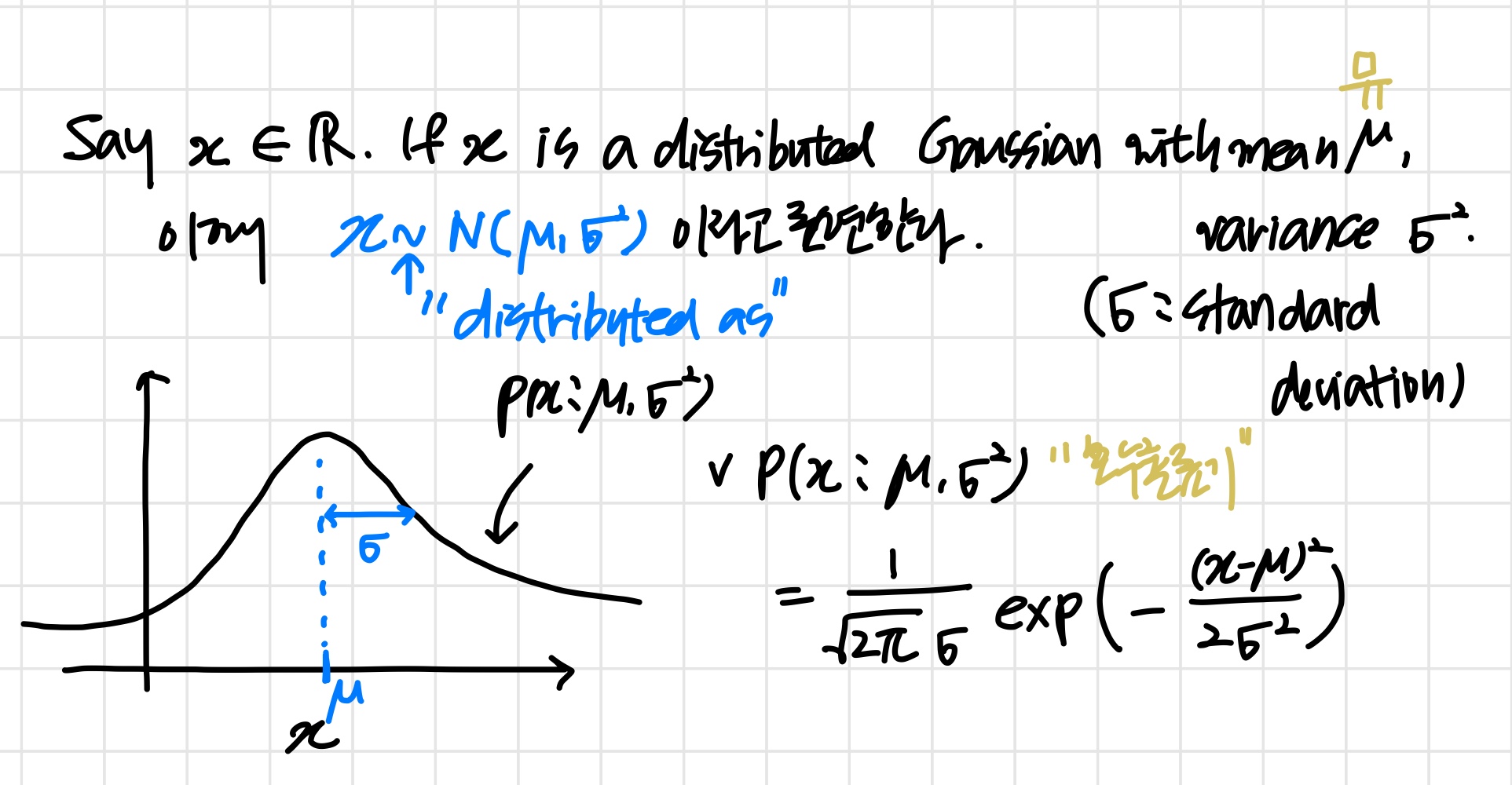
Gaussian distribution example
Parameter estimation
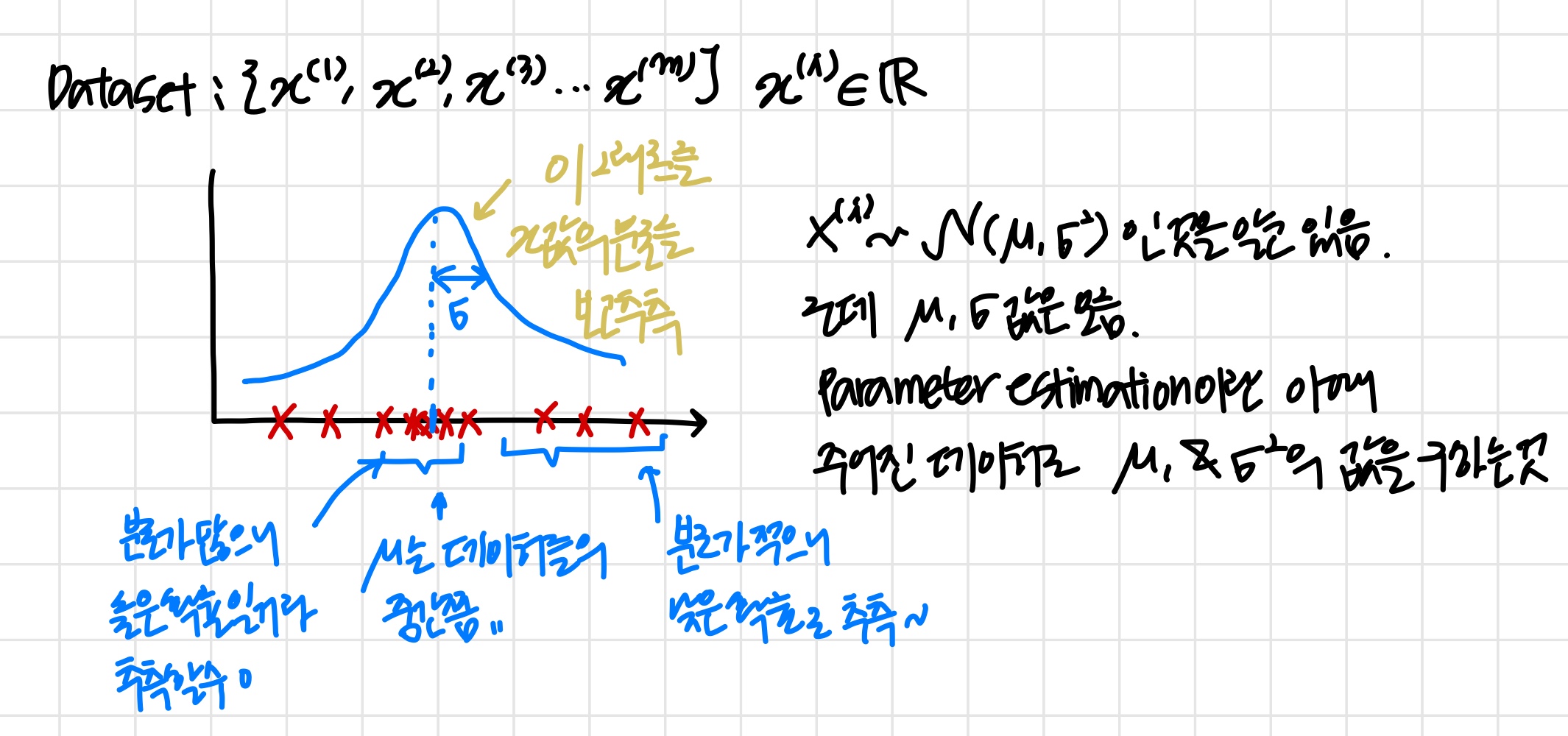
μ 와 σ를 추정하는 방법
- μ=m1∑i=1mx(i)
- σ2=m1∑i=1m(x(i)−μ)2
'데이터가 주어졌을 때 Gaussian~을 따른다면 평균&표준편차를 추정할 수 있다.'
3) Algorithm
Density estimation

Anomaly detection algorithm
-
anomalous 데이터를 식별할 수 있을 것으로 판단되는 특성 xi들을 선택한다.
-
Fit parameters μ1,...,μn,σ12,...σn2
- μj=m1∑i=1mxj(i)
- σj2=m1∑i=1m(xj(i)−μj)2
-
새로운 데이터 x가 주어지면, 아래와 같이 p(x)를 계산한다.
- p(x)=∏j=1nP(xj;μj,σj2)=∏j=1n2πσj1exp(−2σj2(xj−μj)2)
이때 p(x)<ϵ 이면 해당 데이터는 anomaly
Anomaly detection example