[RWKV] Reinventing RNNs for the Transformer Era: RWKV 리뷰

INTRODUCTION

• NLU, 대화형 AI, 시계열 분석, 심지어 이미지나 그래프와 같이 indirectly sequential한 데이터의 분석까지, 두 개의 predominant 알고리즘이 지배했음
  • RNN: 작은 메모리 소요, 그러나 시간 차원에 대한 병렬 처리 문제와 기울기 소실로 인한 시퀀스 길이 제약
  • Transformer: Self-attention 병렬 처리를 통한 효율적 학습 및 긴 시퀀스 길이, 그러나 quadratic complexity로 인한 엄청난 메모리 소요
• 이 두 메커니즘의 장점은 강화하고, 단점은 완화한 알고리즘이 바로 Receptance Weighted Key-Value, 즉 RWKV
  
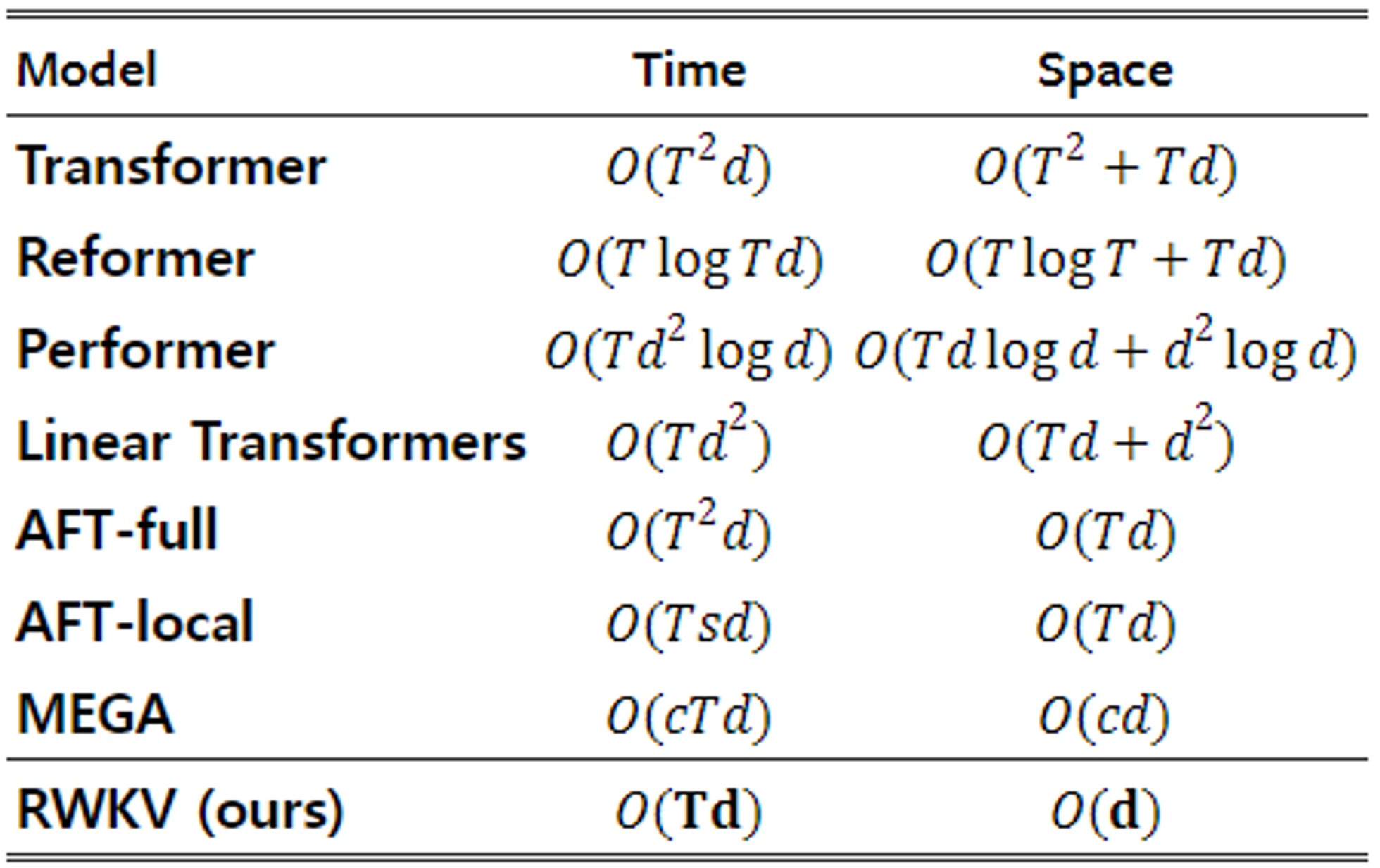
  • Linear scaling을 통해 트랜스포머의 메모리 병목과 quadratic scaling을 완화
  • 그러면서도 robust scalability나 병렬 학습 등의 장점은 살릴 수 있도록 함
  • Attention을 linear attention의 변형으로 재구성하여, 더 효율적인 channel-directed attention으로 사용

BACKGROUND

Recurrent Neural Networks (RNNs)

• 두 개의 linear 블록($W$와 $U$)을 이용한 LSTM의 형태
• 직전 time step과 dependent하기 때문에 병렬화가 불가능함
  • Masked attention의 개념과 달리, 실제로 모델 내에 미래 시퀀스를 고려할 수 있는 term 자체가 없음

Transformers and AFT

• Transformer (Vaswani et al., 2017)
  $\text{Attn}(Q,K,V)=\text{softmax}(QK^\top)V \\ \text{Attn}(Q,K,V)_t=\frac{\Sigma^T_{i=1}e^{q^\top_tk_i}\odot v_i}{\Sigma^T_{i=1}e^{q^\top_tk_i}}$
  • Multi-head attention에서는 $\text{Attn}$에 $1/\sqrt{d_k}$로 스케일링을 해주긴 하지만, 어쨌든 $QK^\top$이 병렬 벡터 연산을 가능케하는 핵심
• Attention-Free Transformer (AFT; Zhai et al., 2021)
  $\text{Attn}^+(W,K,V)_t=\frac{\Sigma^t_{i=1}e^{w_{t,i}+k_i}\odot v_i}{\Sigma^t_{i=1}e^{w_{t,i}+k_i}}$
  • 2021년에 발표된 AFT는 $Q$와 $K$에 대한 행렬곱 형태가 아닌, $W$와 $K$의 덧셈을 통해 연산
  • 이때 $W$는 $\{w_{t,i}\in R^{T\times T}\}$ 형태의 pair-wise position biase이며, $w_{t,i}$는 스칼라
• RWKV attention의 interactive weight $w_{t,i}$
  $w_{t,i}=-(t-i)w$
  • 이때 $w$는 $w\in(R_{\geq0})^d$이고, $d$는 채널의 개수
  • AFT의 attention과 유사하게 접근하되 살짝 변형시켜, interaction weight $w_{t,i}$를 RNN의 형태로 나타낼 수 있도록 변형해줌
  • RWKV의 $w_{t,i}$는 channel-wise 시간 감쇠(time decay) 벡터에 상대 위치를 곱한 값으로, 현재 시간으로부터 감쇠하면서 역추적하게 됨
  • 즉, $w$가 음수가 아닌 경우 $e^{w_{t,i}}\leq1$이 되어 시간이 역행할 수록 per-channel 가중치 $w$가 감쇠한다는 것
• 쉽게 말해, RNN은 time step에 dependent하게 status가 변하게 되고 이로 인해 병렬 연산이 어려운 것인데, 이 시간 축 자체를 하나의 차원을 가지는 벡터로 변환했기 때문에 병렬 연산이 가능
  • 일종의 positional encoding(PE)같은 개념인데, 이게 PE처럼 constant가 아니라 RNN에 기반해 연산되는 일종의 차원 변수가 되는 것

RWKV

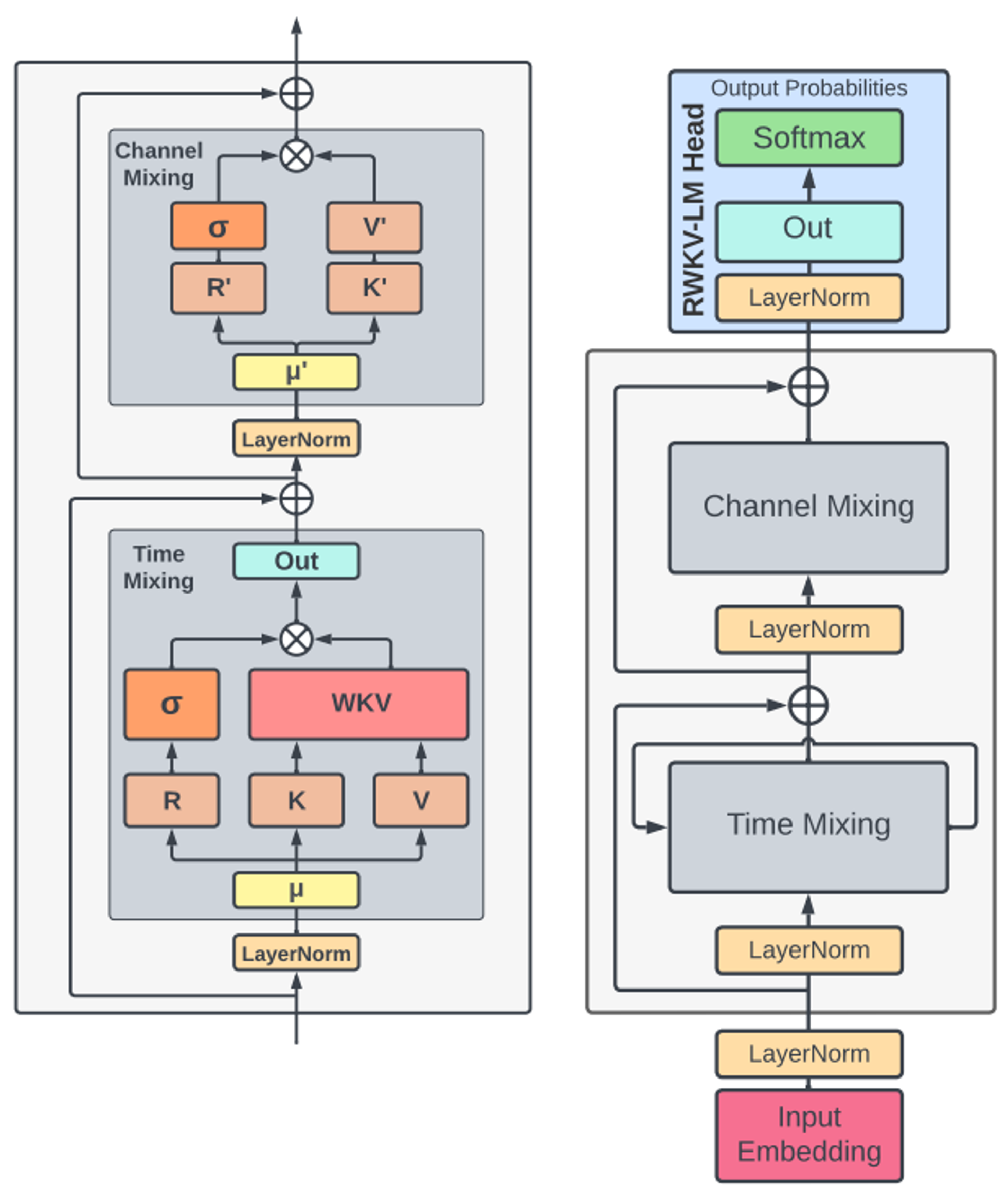
• RWKV 모델은 time-mixing과 channel-mixing의 재료로 사용되는 다음 4개의 기본 요소로 구성
  • $R$: 과거의 정보를 수신해오는 ‘Receptance’ 벡터
  • $W$: Trainable한 위치 ‘Weight’ 감쇠 (positional weight decay) 벡터
  • $K$ & $V$: 트랜스포머의 ‘Key-Value’와 동일

Architecture

• RWKV는 time-dependent softmax 연산을 통해 연산 안정성을 개선하고 기울기 소실을 완화하는 attention-like score를 사용
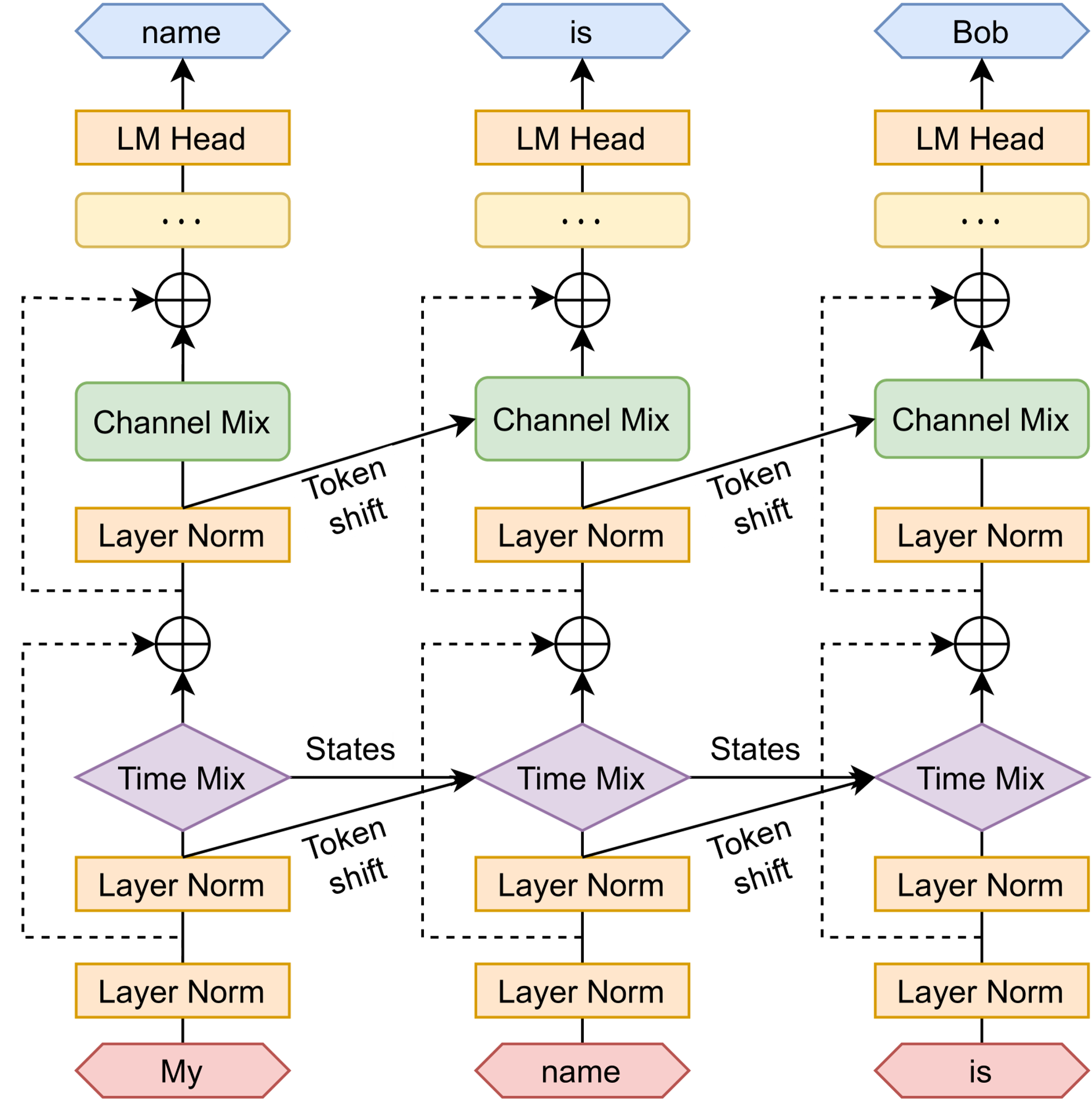
  • 기울기는 가장 관련도가 높은 path를 따라서 전파되고, 블록 내의 layer norm이 기울기를 안정화하여 폭발하거나 소실되지 않도록 함
  • 이러한 residual + normalization 구조를 통해 기존 RNN 보다 효과적으로 적층할 수 있고 패턴 인식 성능을 끌어올릴 수 있다고 함

[Token Shift]

• Time-mixing
  $r_t=W_r\cdot(\mu_r\odot x_t+(1-\mu_r)\odot x_{t-1}), \\ k_t=W_k\cdot(\mu_k\odot x_t+(1-\mu_k)\odot x_{t-1}), \\ v_t=W_v\cdot(\mu_v\odot x_t+(1-\mu_v)\odot x_{t-1}),$
• Channel-mixing
  $r'_t=W'_r\cdot(\mu'_r\odot x_t+(1-\mu_r')\odot x_{t-1}), \\ k'_t=W'_k\cdot(\mu'_k\odot x_t+(1-\mu'_k)\odot x_{t-1})$
• Time-mixing 블록의 $R$, $K$, $V$, channel-mixing 블록의 $R'$, $K'$와 같은 모든 선형 투영 벡터들은 현재 time step과 이전 time step 간의 선형 보간으로 생성되기 때문에, token shift가 용이함
• 실제 코드 상에서는 torch.nn.ZeroPad2d((0,0,1,-1))을 이용해 아주 간단한 시간 차원의 단순 offset으로 구현됨
• 쉽게 말해, 원래 RNN에서는 자연스레 토큰을 하나씩 지나치면서 시간이라는 요소를 학습했다면, RWKV는 시간 축 자체가 벡터로 존재하기 때문에 그 시간을 인위적으로 흐르게 만들기 위해 시퀀스에서 토큰을 앞에서부터 하나씩 잘라가면서 (뒤에는 패딩 추가) 위치를 바꿔준다는 의미

[WKV Operator]

• WKV operator는 AFT와 굉장히 비슷하게 구성돼있지만, $W$를 pairwise 행렬이 아닌 상대적 위치에 대한 channel-wise 벡터로써 사용한다는 것이 차이점
• $WKV$ 벡터는 time-dependent하게 업데이트되며 recurrent한 거동을 갖게됨
• $W$의 잠재적 성능 저하를 피하기 위해, 현재 토큰에 별도로 attend하는 벡터 $U$를 도입하게됨 (후술)

[Output Gating]

• Receptance $r$의 activation을 이용하여, time-mixing과 channel-mixing 블록 모두에서 gating을 해주게 됨
• Activation function은 squared ReLU(So et al., 2021)를 사용했다고 함

Transformer-like Training

• Time-parallel 모드를 통해, RWKV는 트랜스포머처럼 병렬 학습을 수행할 수 있음
  • 1개 layer에서 하나의 시퀀스 배치를 처리하는데에는 $O(BTd^2)$의 시간 복잡도 소요
    • $\lambda\in\{r,k,v,o\}$인 $W_\lambda$의 행렬 곱으로 구성됨 (시퀀스 개수 $B$, 최대 토큰 수 $T$, 채널 $d$)
  • 반대로, $wkv_t$ attention의 업데이트에는 serial scan을 통해 $O(BTd)$의 복잡도만이 소요됨
• 전통적 트랜스포머에서는 $\lambda\in\{Q,K,V,O\}$인 $W_\lambda$를 병렬화
  • $WKV$의 element-wise 연산은 time-dependent 하면서도 병렬화가 가능함
  • 왜? 시간 축 마저 하나의 차원으로 들어갔기 때문

RNN-like Inference

• RNN은 보통 $t$ 시점의 output을 $t+1$ 시점의 input으로 ‘recurrent’하게 사용함

  • 이는 LM의 auturegressive decoding 추론 과정과 흡사함
  • 과거 시점까지의 모든 토큰들에 기반해 다음 나올 가장 높은 확률의 토큰을 계산하니까

• RWKV는 이런 RNN-like한 구조의 장점, time-sequential 모드를 채택함

  

  $a_0=b_0=0, \\ wkv_t=\frac{a_{t-1}+e^{u+k_t}\odot v_t}{b_{t-1}+e^{u+k_t}}, \\ a_t=e^{-w}\odot a_{t-1}+e^{k_t}\odot v_t,\quad b_t=e^{-w}\odot b_{t-1}+e^{k_t}$

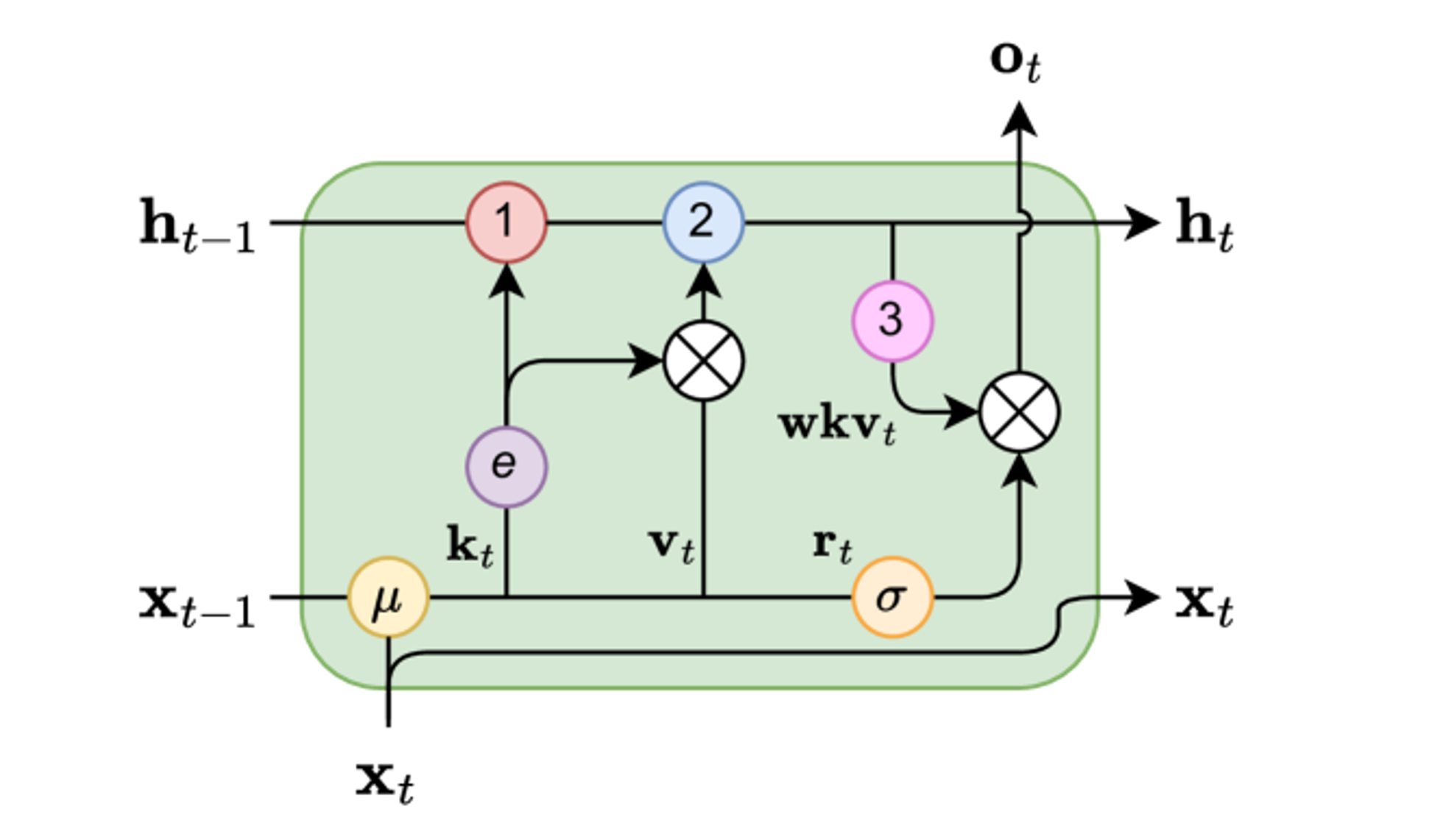
  • Time-mixing 블록을 이용해 recursive decoding을 구현

  • 위 수식을 그대로 이용하면 $e^{k_t}$를 계산할 때 overflow가 발생할 수 있는데, 이를 방지하기 위해 아래와 같은 수치적 트릭을 사용하게 됨

    $q:=\max(p_{t-1},u+k_t), \\ wkv_t=\frac{e^{p_{t-1}-q}\odot a'_{t-1}+e^{u+k_t-q}\odot v_t}{e^{p_{t-1}-q}\odot b'_{t-1}+e^{u+k_t-q}}$

  • 이때, $a_1=e^{k_1}\odot v_1$, $b_1=e^{k_1}$이고, $a'_1=v_1$, $b'_1=1$, $p_1=k_1$이며, $p_t$는 $a_t$와 $b_t$의 공유 지수(shared exponents)를 저장하는 역할이 됨

  • $a'_t$와 $b'_t$, 그리고 그들의 공유 지수도 비슷한 방식으로 계산됨

    $q':=\max(p_{t-1}-w,k_t), \\ a'_t=e^{p_{t-1}-w-q'}\odot a'_{t-1}+e^{k_t-q'}\odot v_t \\ b'_t=e^{p_{t-1}-w-q'}\odot b'_{t-1}+e^{k_t-q'}, \\ p_t=q'$

  • 이러한 수식들을 통해, $D$차원의 모델에 대해 다섯 개의 요소로 구성된 internal state를 표현

    • $x_t$: Time-mix 블록의 현재 입력
    • $y_t$: Channel-mix 블록의 현재 입력
    • $a'_t$: $WKV$ 값의 numerator
    • $b'_t$: $WKV$ 값의 denominator
    • $p_t$: $WKV$ 연산의 numerical precision 보존을 위해 사용되는 보조 status

Additional Optimizations

[Custom CUDA Kernel]

• WKV 연산은 sequential한 특성 때문에 기존 딥러닝 프레임워크로 연산하기에 다소 비효율적인 면이 있어서, 커스텀 CUDA 커널을 따로 개발해서 사용
  • 학습 가속기에서 딱 하나만 sequential한 연산 커널을 실행시키고, 나머지 행렬곱이나 point-wise operation은 병렬화되어 효율성 확보

[Small Init Embedding]

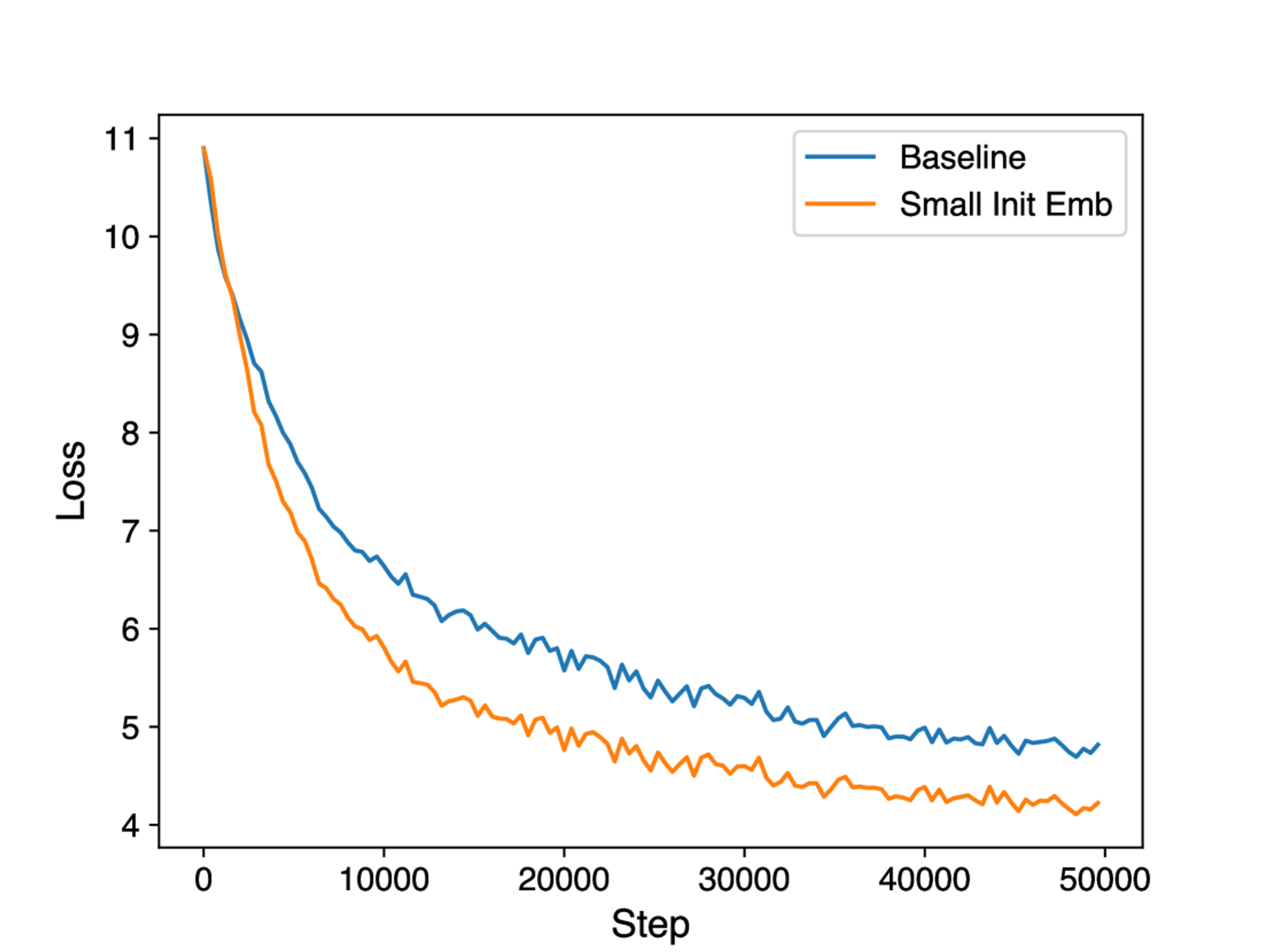
• 트랜스포머는 원래 훈련 초기에 embedding 행렬이 매우 느리게 업데이트된다고 함
  • 이를 해결하기 위해 초기화를 작은 값으로 수행한 후, layer norm 연산을 적용
  • 안정성에 도움을 주면서 임베딩의 빠른 업데이트와 향상된 수렴성을 보임

[Custom Initialization]

• 명확한 정보 흐름을 위해 symmetry를 깨고, identity mapping과 유사한 값으로 초기화
  • 대부분의 가중치는 0으로 초기화되며, linear layer에는 bias를 제거

TRAINED MODELS AND COMPUTING COSTS

Additional Training Details

• 정확한 모델 별 가중치 개수는 다음과 같음
  $\text{\# parameters}=2VD+13D^2L+D(11L+4)$
  • v1의 $V$는 50,277 (vocab_size), $D$와 $L$은 위 표와 같음
• 학습에는 weight decay 없는 Adam을 사용하나, learning rate에 exponential decay를 적용
  • ㄱ자처럼 구성되어서, 초기에는 높은 수치로 일정하게 유지되다 급락하는 형태
• 단순 CE loss를 보완하기 위해 PaLM(Google, 2022)에서 사용했던 변형 버전의 CE loss 사용
  • 보조 loss가 추가되어, softmax normalizer가 0에 가깝게 근사되도록 유도
• BrainFloat-16Bit (BF16) 사용
• Context length는 1k로 우선 제한

Scaling Laws

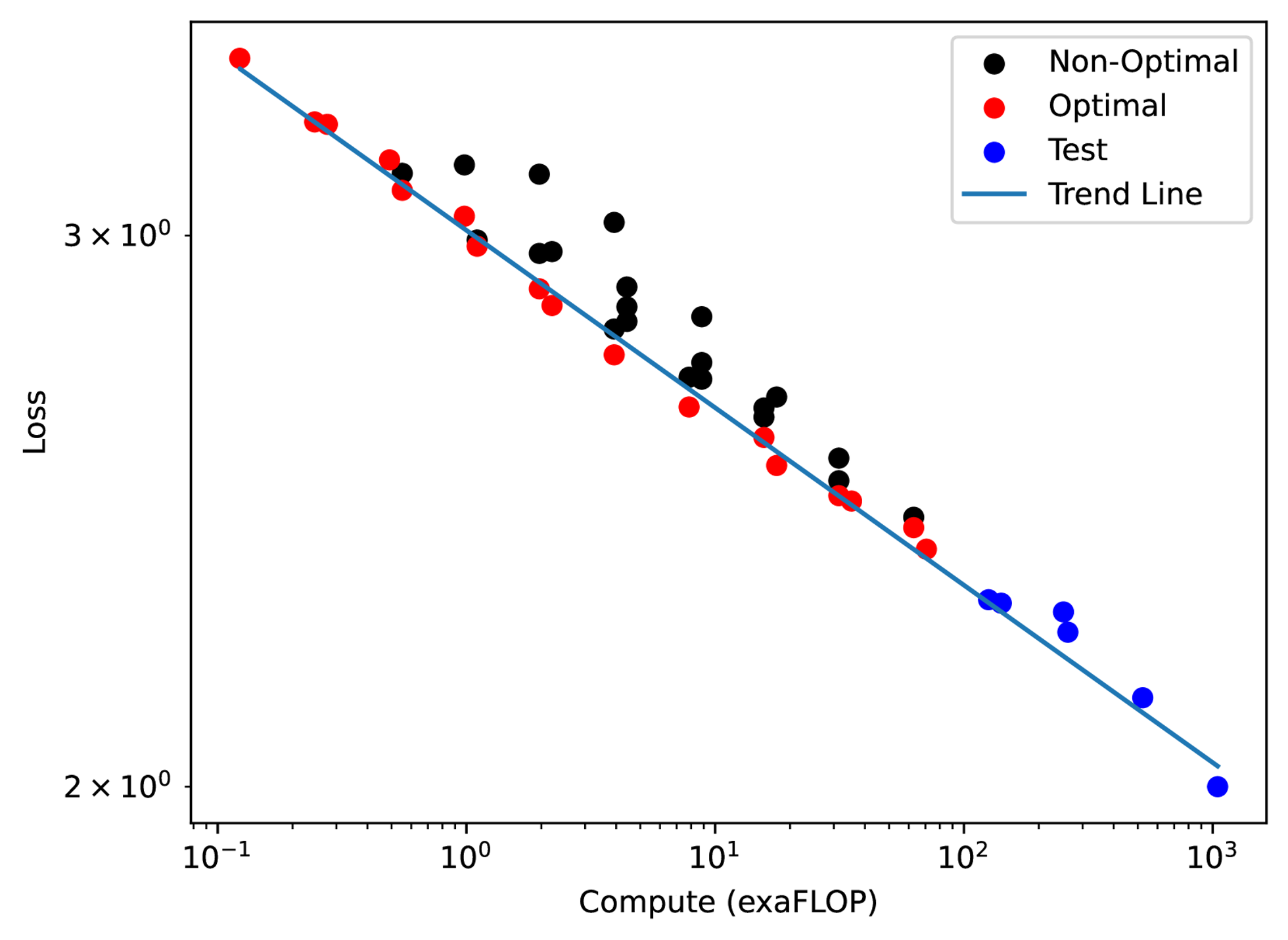
• Scaling law에는 모델 크기 $N$, 데이터셋 크기 $D$, 최적 연산 비용 $C_{\min}$ 등이 영향을 미칠 수 있음
  • 비용과 성능에 대한 예측 및 계획을 세울 수 있게 하고, 실패하더라도 향후 연구에 많은 피드백을 제공해줄 수 있음
• LSTM은 트랜스포머와 다르게 log-log linear scaling을 엄격히 따르지 않는다는 선행 연구가 있었음 (OpenAI, 2020)
  • 그러나, 여러 dataset-parameter 조건을 다르게 하여 45개의 RWKV 모델을 학습시킨 결과, RWKV는 트랜스포머와 동일한 scaling law를 따른다고 밝혀짐
  • 연산 비용과 loss에 대한 Pareto 최적점에 대한 log-log 선형 적합도는 0.994의 $r^2$값을 가짐

EVALUATIONS

• RWKV의 성능을 두 가지 주요 관점에서 바라봄
  • Competitiveness: 동일한 연산 비용의 quadratic 트랜스포머와 비교했을 때 괜찮은가?
  • Long context: 기존 RNN이 해결할 수 없었던 long-term dependency를 해결했는가?

NLP Evaluations

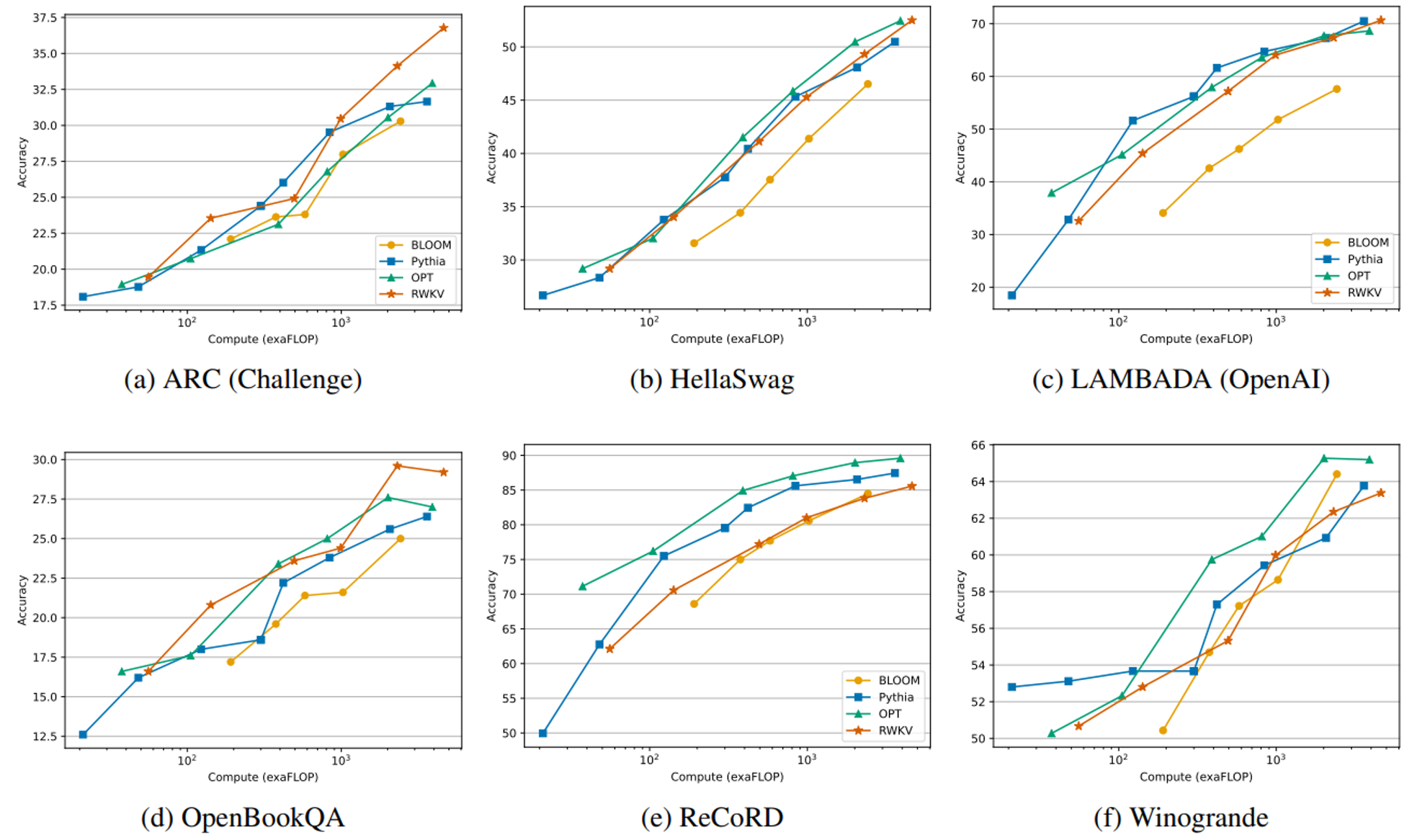
• 비슷한 수의 토큰(~330B)으로 훈련시킨 Pythia, OPT, BLOOM과 비교
• 성능은 FLOPs 기준으로 비교했을 때 비교군과 비슷하거나 약간 부족한 모습
  • 특이한 점으로는 ChatGPT/GPT-4와 비교 실험 당시 GPT보다 프롬프트에 상당히 민감하게 반응하는 모습이 있었음
  • GPT 프롬프트에서 RWKV에 더 적합한 방식으로 재배치(re-order)했을 때 F1 score가 44.2%에서 74.8%로 증가한 경우도 있다고 함

Extended Context Finetuning

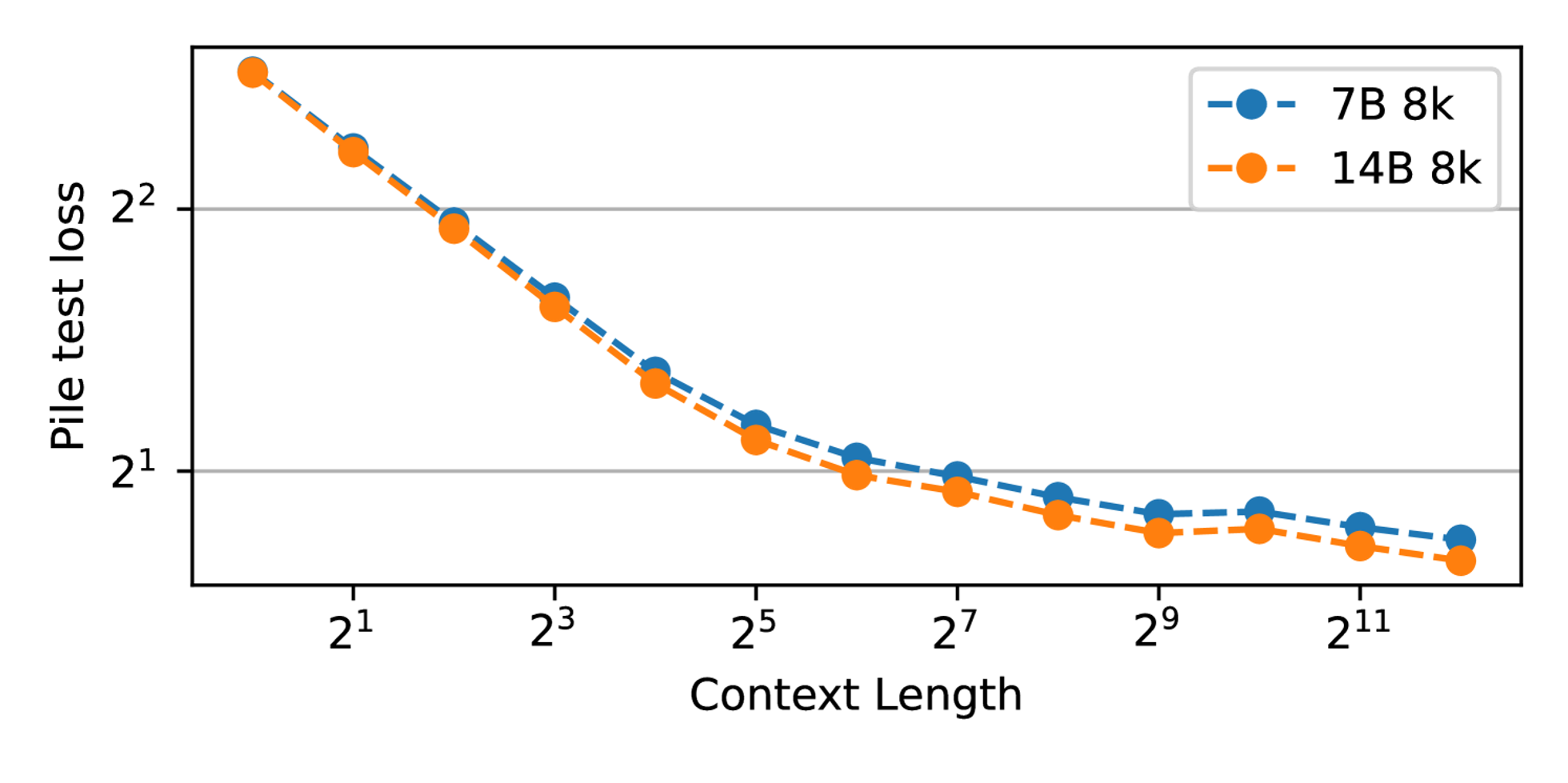
• 사실 RNN은 positional embedding이 따로 없기 때문에, 기본적으로 정해진 context length가 없음
  • 그러나 어찌됐든 효율적인 병렬/배치 학습을 위해서는 context length를 지정해주는 것이 좋음
• RWKV에서는 curriculum learning과 비슷하게 context length를 늘려가는 학습을 했다고 함
  1. 첫 10B 토큰에서는 [1k, 2k] 범위의 시퀀스
  2. 다음 100B 토큰은 [2k, 4k] 범위의 시퀀스
  3. 다음 100B 토큰은 [4k, 8k] 범위의 시퀀스
  • 와 같은 형태로 The Pile 말뭉치를 학습했다고 하며, 안정적으로 loss가 감소하는 모습을 보였다고 함
• 사실 RWKV가 처음 나온 2023년 당시에는 8k가 LLM의 최고 context length 였고, 이후 2024년에는 LongRoPE와 InfiniLM 등이 등장하면서 128k~2M까지 어쩌면 거의 무제한의 context length를 갖게 되었음

INFERENCE EXPERIMENTS

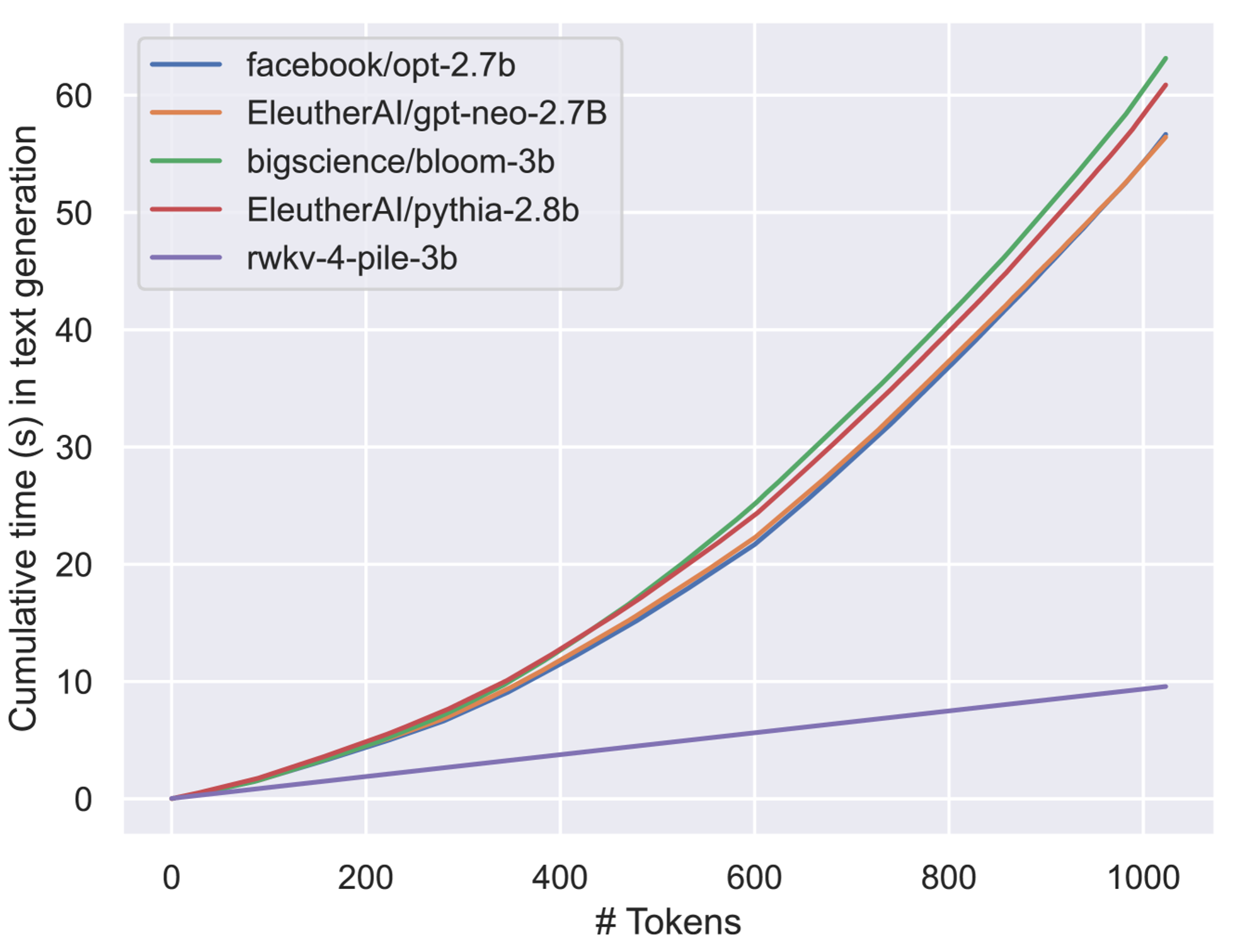
• x86 CPU와 A100 80GB GPU를 탑재한 일반적인 컴퓨팅 플랫폼에서 생성 속도 및 메모리를 확인

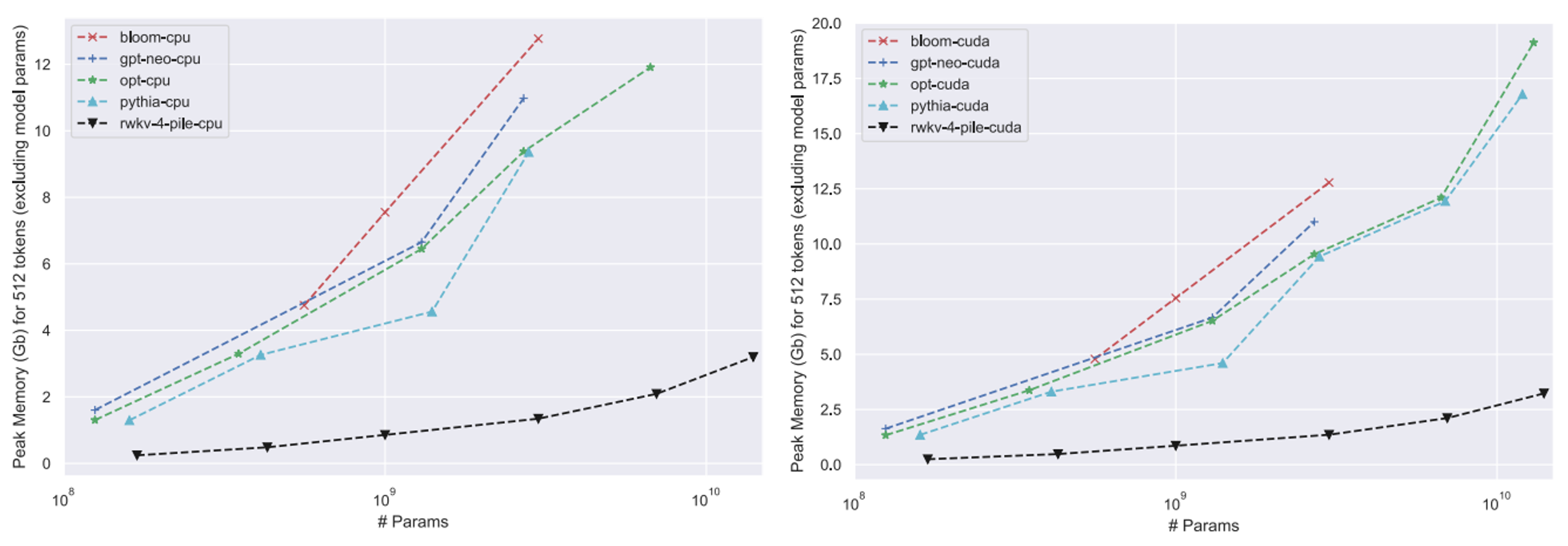
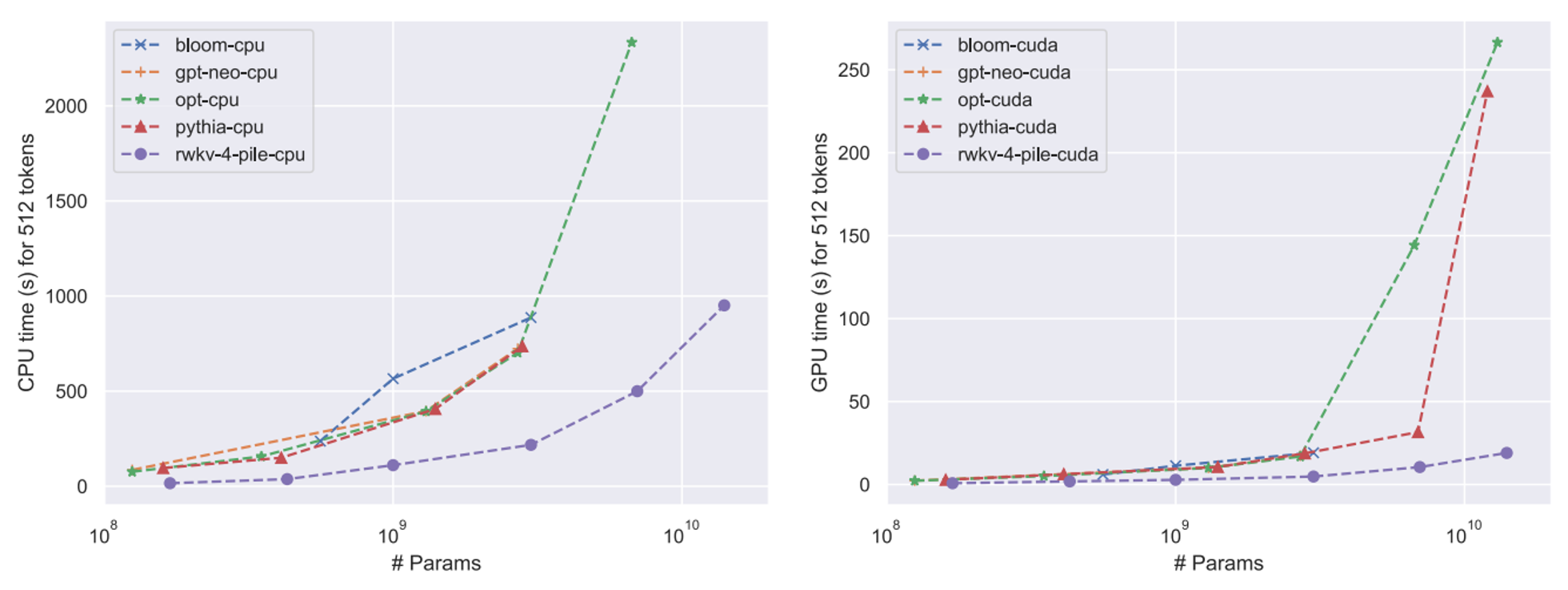
• 10B 이상의 모델임에도 메모리는 약 3GB, 추론 속도는 30초가 채 걸리지 않는 괴랄한 성능을 보여줌 (GPU 기준)