[Hands-on Machine Learning] Regularization (L1, L2, Elastic Net)

김강태·2021년 1월 29일

Regularization

이전에 보았던 high variance로 인한 overfitting을 감소시키는 방법 중 하나로 regularization이 있었다.
Linear regression model 에서는 보통 모델의 weights에 penelty를 주어 규제를 가한다. 이러한 방법을 weight decay라고도 한다. 3가지의 각기다른 규제를 살펴보자.

1. Ridge Regression (L2 regularization)

* loss function of Ridge regression

J(\theta) = MSE(\theta) + \alpha\frac{1}{2}\sum_{i=1}^n \theta^2_i

위 수식은 규제한 $\alpha\frac{1}{2}\sum_{i=1}^n \theta^2_i$ 가 추가된 선형회귀의 loss function이다.
이때 hyperparmeter인 $\alpha$ 를 통해 모델을 얼마나 규제할지 조절하며 bias인 $\theta_0$ 는 규제되지 않는다.
$\bold{w}$ 를 feature에 대한 weights vector ( $\theta_1$ ~ $\theta_n$ )라고 했을때 reguralization term은 $\frac{1}{2}(\| w \|_2)^2$ 과 같다. 이때 $\|\cdot\|_2$ 는 L2 norm을 뜻한다.
L2 regularization은 학습시에 이전 step의 weights에 매번 각 weight element별 $\alpha$ % 만큼을 빼주는 형태이다.

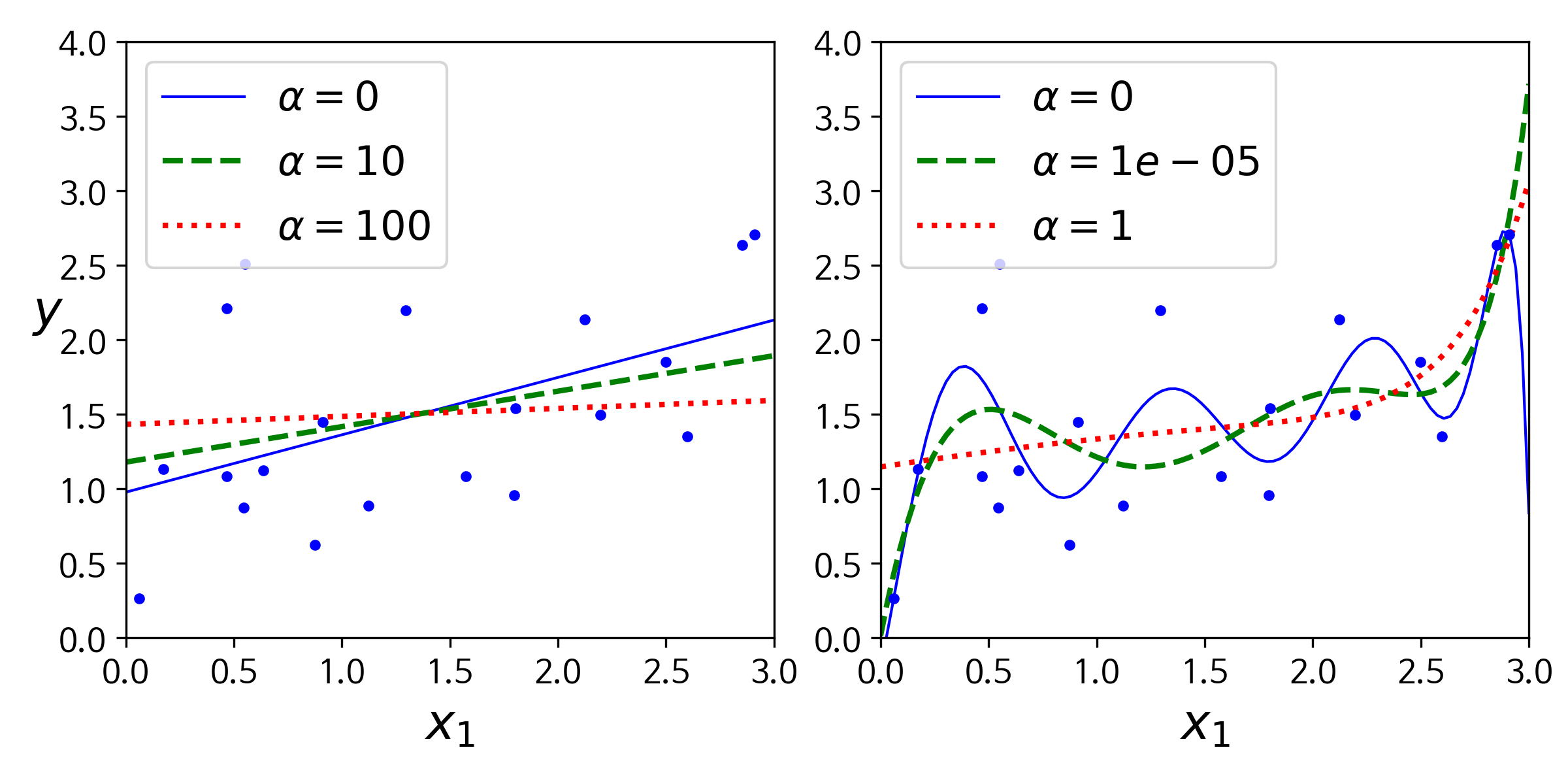
위 그림은 linear model과 polynominal model(degree=10)에 다른 $\alpha$ 를 적용하여 Ridge model을 훈련시킨 결과이다.
오른쪽 polynominal model을 보았을때 $\alpha$ 를 증가시킬 수록 점점 linear model에 근접하는 것을 볼수있는데. 이는 $\alpha$ 가 증가할 수록 weight에 대한 penalty가 커지고 이에따라 각 feature에 대한 weight값(coefficient)이 0에 수렴하기 때문이다.
이러한 Ridge regression도 linear regression처럼 정규방정식으로 나타낼 수 있다.

* normal equation of Ridge regression

\hat{\theta} = (X^TX+\alpha A)^{-1}X^Ty

* 위 식에서 A는 bias에 해당하는 맨 왼쪽 원소가 0인 (n+1)x(n+1)의 identity matrix이다.

다음은 sklearn에서 정규방정식을 사용한 ridge regression을 적용하는예 이다

from sklearn.linear_model import Ridge

X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5

ridge_reg = Ridge(alpha=1, slover='choloesky')
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]])

array([[1.55071465]])

다음은 SGD를 사용한예 이다

sgd_reg = SGDRegressor(max_iter=50, penalty="l2", tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])

array([1.56516218])

2. Lasso Regression (L1 regularization)

J(\theta) = MSE(\theta) + \alpha\frac{1}{2}\sum_{i=1}^n |\theta_i|

* loss function of Lasso regression

Lasso regression은 ridge regression처럼 loss function에 regularization term을 더해주지만 $l_2$ norm 대신 $l_1$ norm을 사용한다.
$l_1$ norm을 penalty로 사용하는 lasso는 ridge와 다르게 학습시 (gradient descent 적용할때) 덜 중요한 feature의 weight를 0으로 만든다는 점이다.
* 이때 덜 중요한 feature의 weight라는 말은 값이 0에 가까워 영향이 적은 weight를 말하고 학습시 l1 penelty를 통해 0으로 유도된다는 것 이다. 이는 l1 regularization이 학습시 자동으로 feture selection을 하여 sparse model을 만들게 된다.
하지만 l1 regularization term을 포함한 lasso의 loss function은 ( $\theta_i = 0$ ) 일때 불연속성을 가져 미분가능하지 않기때문에 weight에 sign function(부호함수)를 취하여 gradient descent 에 적용시킨다.

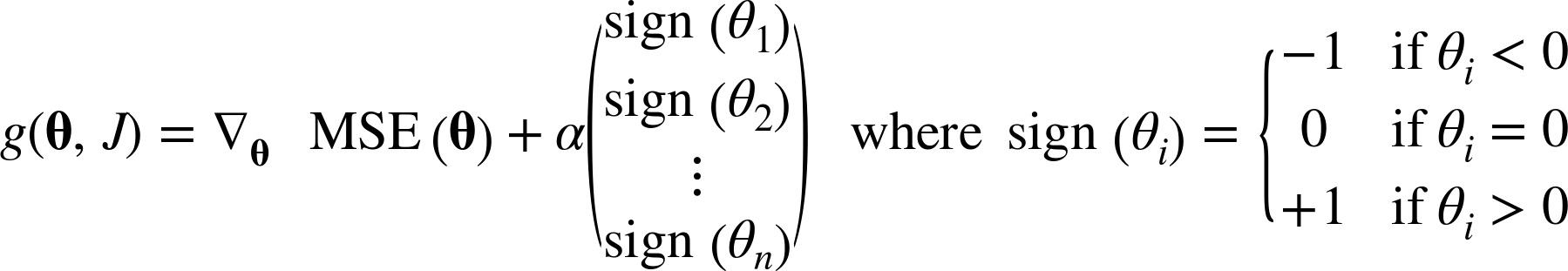
다음은 Lasso 클래스를 사용한 간단한 sklearn 예제이다

from sklearn.linear_model import Lasso

lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])

array([[1.55788174]])

3. Elastic net

Elastic net은 l1 penelty를 사용한 Lasso와 l2 penelty를 사용한 Ridge를 합쳐 서로 절충한 모델이다.
Ridge와 Lasso regularization term을 단순히 더한 후 비율을 r을 통해 조정하여 사용한다. 식은 아래와 같다.

J(\theta) = MSE(\theta) + r\alpha\sum_{i=1}^n |\theta_i| + \frac{1-r}{2}\alpha\sum_{i=1}^n \theta_i^2

보통의 경우에 default로 Ridge를 사용하지만 문제가 있다고 생각될 때 lasso나 elastic net을 사용한다. feature 수가 training sample 수 보다 많을 경우 lasso보다 elastic net을 사용한다.
다음은 ElasticNet을 사용한 간단한 sklearn 예제이다

from sklearn.linear_model import ElasticNet

elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])

array([[1.54333232]])

4. Early stopping.

gradient descent와 같은 반복적인 학습 algorithm을 규제하는 또다른 방식은 valid error가 최솟값에 도달하면 학습을 중지시키는 것이다. 이를 early stopping 이라고 한다.

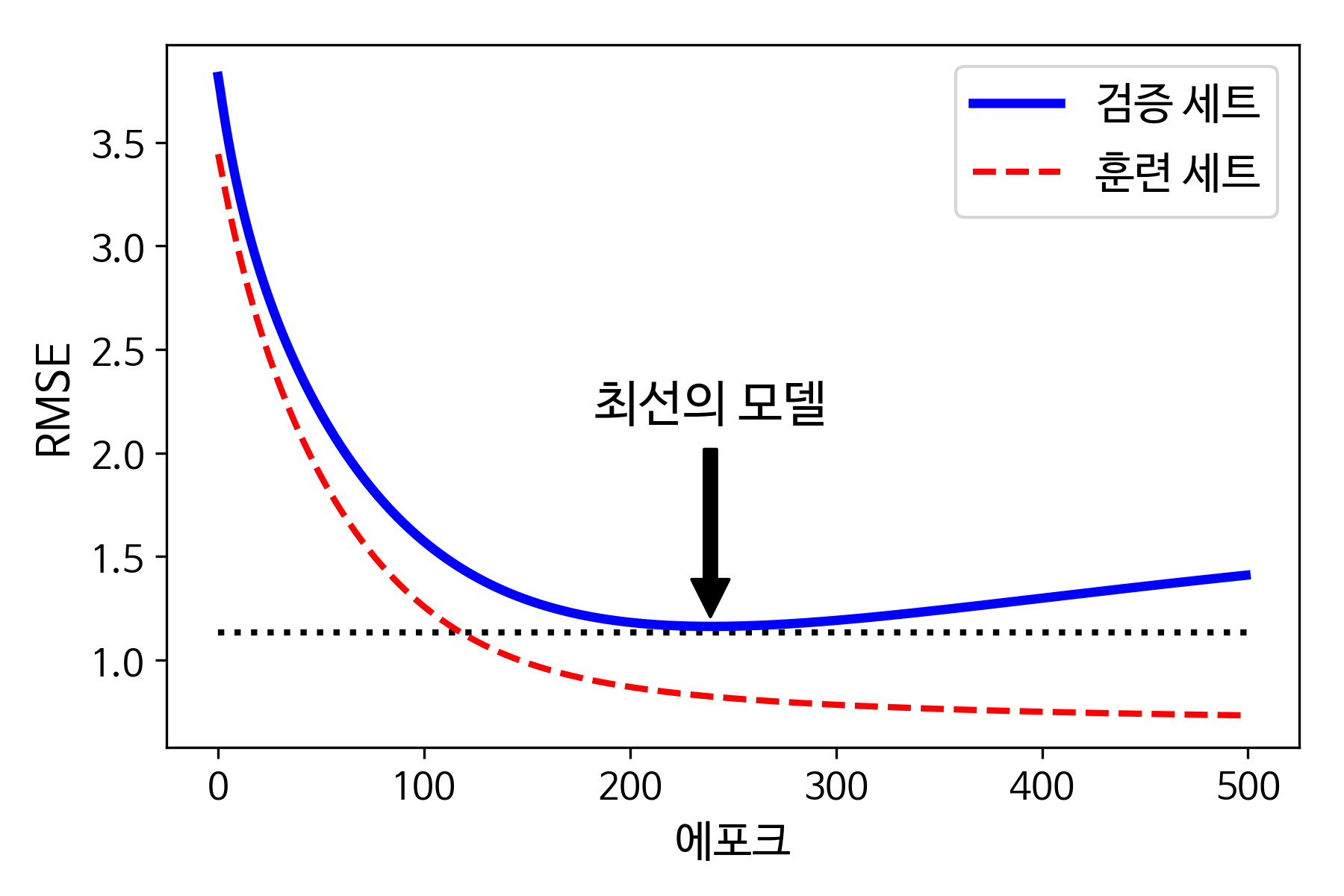
위 그림처럼 epoch가 진행됨에 따라 학습되며 train set 과 valid set의 error가 줄어들다가 valid set이 어느 지점부터 다시 상승하는 것을 볼 수 있는데. 이는 overfitting 되고있다는 뜻이고 early stopping을 통해 error가 최소에 도달 하는 지점에서 훈련을 멈추는 것 이다.