[혼공머신] 합성곱 신경망의 시각화

[혼자 공부하는 머신러닝+딥러닝] 책에 기반한 정리글입니다.
전체 소스코드는 아래 Github 링크에서 확인할 수 있습니다.

Github 링크

0. 개요

이번 편에서는 저번 편에서 저장한 합성곱 신경망 모델을 읽어 들인 후 모델의 가중치와 특성 맵을 시각화해본다. 또한 케라스의 함수형 API를 사용하여 모델의 조합을 자유롭게 구성해본다.

1. 데이터 준비

이전에 훈련한 합성곱 신경망 모델을 불러온다.

from tensorflow import keras
model = keras.models.load_model('best-cnn-model.h5')

케라스 모델에 추가한 층은 layers 속성에 저장되어 있다.

model.layers

출력
[<keras.layers.convolutional.Conv2D at 0x7f803f8dad90>,
 <keras.layers.pooling.MaxPooling2D at 0x7f7fc61459d0>,
 <keras.layers.convolutional.Conv2D at 0x7f7fc60eed10>,
 <keras.layers.pooling.MaxPooling2D at 0x7f7fc60eee90>,
 <keras.layers.core.flatten.Flatten at 0x7f7fc6085c10>,
 <keras.layers.core.dense.Dense at 0x7f7fc60eeb90>,
 <keras.layers.core.dropout.Dropout at 0x7f7fc608a450>,
 <keras.layers.core.dense.Dense at 0x7f7fc607c990>]

첫 번째 합성곱 층의 가중치를 조사해 본다. 층의 가중치와 절편은 층의 weights 속성에 저장되어 있다.

conv = model.layers[0]
print(conv.weights[0].shape, conv.weights[1].shape)

출력 (3, 3, 1, 32) (32,)

커널 크기가 (3,3,1)이며 필터 개수가 32개이므로 첫 번째 원소의 가중치의 크기는 (3,3,1,32)이다.
필터마다 1개의 절편이 있으므로 두 번째 원소의 크기는 (32,0)이다.

한편, weights 속성은 텐서플로의 다차원 배열인 Tensor 클래스의 객체이다.
numpy() 메서드로 넘파이 배열로 변환한 후 가중치 배열의 평균과 표준편차를 구해본다.

conv_weights = conv.weights[0].numpy()

# 평균, 표준편차
print(conv_weights.mean(), conv_weights.std())

출력 -0.019439656 0.23001778

이 가중치의 평균값은 0에 가깝고, 표준편차는 0.23 정도이다. 나중에 이 값을 훈련하기 전의 가중치와 비교해본다.

1. 가중치 시각화하기

1-1. 가중치 분포 히스토그램으로 나타내기

먼저 이 가중치의 분포를 히스토그램으로 그려본다.

import matplotlib.pyplot as plt
plt.hist(conv_weights.reshape(-1,1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()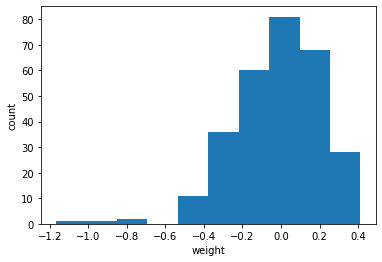

0을 중심으로 종 모양으로 분포됨을 확인할 수 있다.

1-2. 커널 그림으로 나타내기

이번에는 32개의 커널을 16개씩 두 줄에 출력해 본다.

fig, axs = plt.subplots(2, 16, figsize=(15,2))

for i in range(2) :
  for j in range(16) :
  	# 32개의 커널을 16개씩 두 줄에 출력
    axs[i, j].imshow(conv_weights[:,:,0,i*16+j], vmin=-0.5, vmax=0.5)
    axs[i, j].axis('off')

plt.show()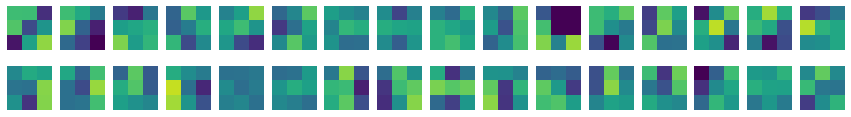

vmin과 vmax 파라미터로 픽셀의 최댓값과 최솟값을 지정하여 컬러맵으로 표현할 범위를 지정한다.
결과를 보면, 이 가중치 값이 무작위가 아닌 어떠한 패턴이 나타난 것을 볼 수 있다. 픽셀의 특정 부분이 밝다거나 하는 식이다.

1-3. 빈 합성곱 신경망의 가중치

위와 같은 방법으로, 훈련되지 않은 합성곱 신경망의 가중치를 조사한다.

no_training_model = keras.Sequential()
no_training_model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu', padding='same', input_shape=(28,28,1)))

no_training_conv = no_training_model.layers[0]
print(no_training_conv.weights[0].shape)

출력 (3, 3, 1, 32)

3x3 커널을 32개 사용했다.

no_training_weights = no_training_conv.weights[0].numpy()
print(no_training_weights.mean(), no_training_weights.std())

출력 -0.0010081615 0.07870515

위의 훈련된 합성곱 신경망과 비교하여 평균은 비슷하지만 표준편차는 매우 작은 것을 알 수 있다.

plt.hist(no_training_weights.reshape(-1,1))
plt.xlabel('weights')
plt.ylabel('count')
plt.show()

대부분의 가중치가 -0.15 ~ 0.15 사이에 있고, 고른 분포를 보이는 것을 알 수 있다.
텐서플로가 신경망의 가중치를 처음 초기화할 때, 균등 분포에서 랜덤하게 값을 선택하기에 이런 분포를 보인다.

이를 그림으로 시각화한다.

fig, axs = plt.subplots(2, 16, figsize=(15,2))

for i in range(2) :
  for j in range(16) :
    axs[i, j].imshow(no_training_weights[:,:,0,i*16+j], vmin=-0.5, vmax=0.5)
    axs[i, j].axis('off')

plt.show()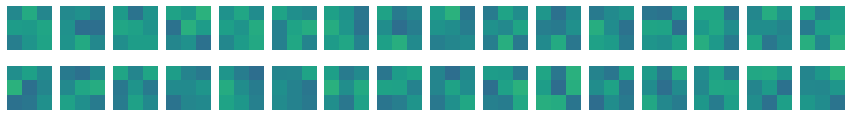

위와 달리 가중치가 밋밋하게 초기화된 것을 볼 수 있다.

이를 통해 합성곱 신경망이 데이터셋의 분류 정확도를 높이기 위해 유용한 패턴을 학습했다는 사실을 알 수 있다.

2. 함수형 API

지금까지 신경망 모델을 만들 때 케라스 Sequential 클래스를 사용했다. 이는 층을 차례대로 쌓은 모델을 만드는데, 딥러닝에서는 좀 더 복잡한 모델이 많이 있어 이런 경우는 Sequential 클래스를 사용하기 어렵다.

대신 함수형 API를 사용한다. 함수형 API는 케라스의 Model 클래스를 사용하여 모델을 만든다.
그 예로, Dense층 2개로 만들어진 완전 연결 신경망을 함수형 API로 구현해본다.

inputs = keras.Input(shape=(784,))

dense1 = keras.layers.Dense(100, activation='signoid')
dense2 = keras.layers.Dense(10, activation='softmax')

hidden = dense1(inputs)
outputs = dense2(hidden)

model = keras.Model(inputs, outputs)

케라스는 InputLayer 클래스 객체를 쉽게 다룰 수 있게 Input() 메서드를 별도로 제공한다.

두 개의 층 dense를 만든 뒤, inputs를 dense1에 통과시켜 출력값 hidden을 만들고, 이를 다시 입력값으로 dense2에 통과시켜 출력값을 만들어 이를 모델화한다.

한편, 특성 맵을 시각화하기 위해서는 첫 번째 층인 Conv2D의 출력이 필요하고, 이는 Conv2D 객체의 output 속성에서 얻을 수 있다.
모델 객체의 input 속성으로 모델의 입력 또한 얻을 수 있다.

이것을 이용하여 model.input과 model.layers[0].output 을 연결하는 새로운 conv_acti 모델을 만들 수 있다.

conv_acti = keras.Model(model.input, model.layers[0].output)

model 객체의 predict() 메서드를 호출하면 입력부터 마지막 층까지의 계산을 수행한 후 최종 출력을 반환하므로, conv_acti의 predict() 메서드를 호출하여 Conv2D의 출력을 반환할 수 있다. 이를 통해 특성 맵을 시각화해 본다.

3. 특성 맵 시각화

케라스 패션 MNIST 데이터셋으로 훈련 세트의 첫 번째 샘플을 그려본다.

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
plt.imshow(train_input[0], cmap='gray_r')
plt.show()

이 샘플을 conv_acti 모델에 주입하여 Conv2D층이 만드는 특성 맵을 출력한다.
입력 차원을 reshape()하고, 255로 나누어 표준화한다.

inputs = train_input[0:1].reshape(-1, 28, 28, 1) /255.0
feature_maps = conv_acti.predict(inputs)

print(feature_maps.shape)

출력 (1, 28, 28, 32)

28x28 크기의 필터 32개로 구성되어 있다. 이를 시각화한다.

fig, axs = plt.subplots(4, 8, figsize=(15,8))

for i in range(4) :
  for j in range(8) :
    axs[i, j].imshow(feature_maps[0,:,:,i*8+j])
    axs[i, j].axis('off')

plt.show()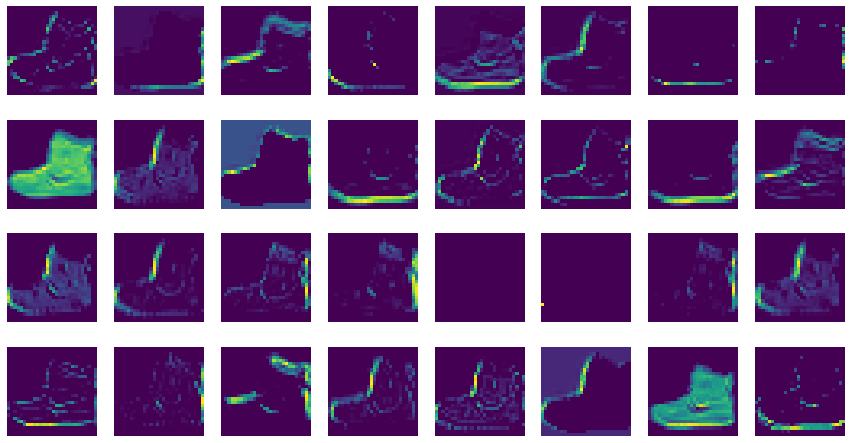

이 특성 맵은 32개의 필터로 인해 입력 이미지에서 강하게 활성화된 부분을 보여 준다.
이전 가중치 시각화와 비교하여 어떤 부분이 크게 활성화되었는지 파악할 수 있다.

두 번째 합성곱 층이 만든 특성 맵도 같은 방식으로 시각화한다.

conv2_acti = keras.Model(model.input, model.layers[2].output)
inputs = train_input[0:1].reshape(-1, 28, 28, 1) /255.0

feature_maps = conv2_acti.predict(inputs)

fig, axs = plt.subplots(8, 8, figsize=(12,12))

for i in range(8) :
  for j in range(8) :
    axs[i, j].imshow(feature_maps[0,:,:,i*8+j])
    axs[i, j].axis('off')

plt.show()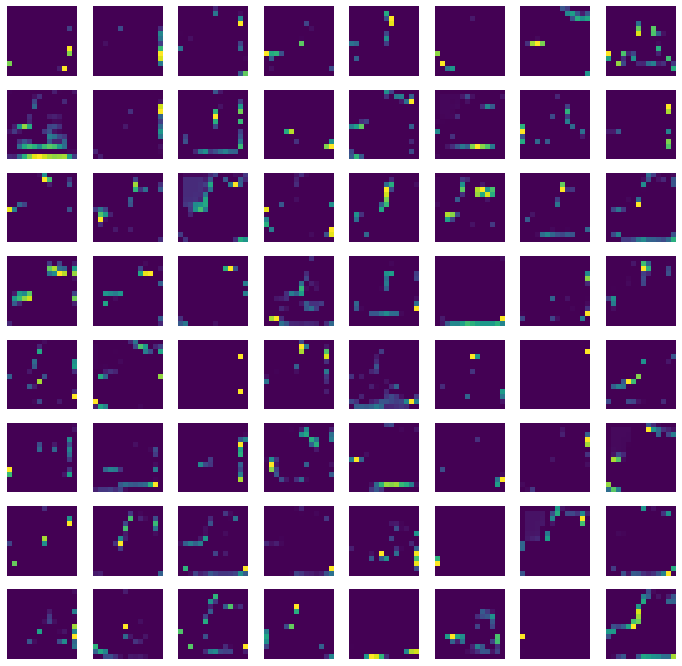

이 특성 맵은 시각적으로 이해하기 어렵다.

이를 통해, 처음의 합성곱 층은 이미지의 시각적인 정보를 감지하고, 뒤쪽에 있는 합성곱 층은 앞쪽에서 감지한 시각적인 정보를 바탕으로 추상적인 정보를 학습한다고 볼 수 있다.