Overview

• In Chapter 11, General Bayesian estimators
  • MMSE takes a simple form when $\text{x}$ and $\theta$ are jointly Gaussian
    $\rightarrow$ it is linear and used only the $1^{st}$ and $2^{nd}$ order moments(mean and covariance)
  • General MMSE(without the Gaussian assumption) requires multi-dimensional integrations to implement $\rightarrow$ undesirable
• In Chapter 12, Linear Bayesian estimators
  • What to do if we can't assume Gaussian but want MMSE?
    • Keep the MMSE criteria, but... restrict the form of the estimator to be LINEAR
    • LMMSE = Wiener Filter

---

Linear MMSE Estimation

• Scalar Paramter Case
  • Estimate $\theta$, a random variable realization
  • Given a data vector $\text{x} = [x[0]\;x[1],\;\cdots,x[N-1]]^T$
  • Assume joint PDF $p(\text{x},\theta)$ is unknown, but the first two moments are known
  • Statistical dependence between $\text{x}$ and $\theta$
  • Goal : Make the best possible estimate while using a linear (or affine) form for the estimator
    $\hat \theta=\sum^{N-1}_{n=0} a_nx[n]+a_N$
  • Choose $a_n$'s to minimize the Bayesian MSE
    $\text{Bmse}(\hat\theta)=E\left[(\theta-\hat\theta)^2\right] \rightarrow \text{linear MMSE estimator}$

---

• Derivation of Optimal LMMSE Coefficients
  $\text{Bmse}(\hat \theta)=E\left[\left(\theta-\sum^{N-1}_{n=0}a_nx[n]-a_N\right)^2\right]$
  • Step 1 : Focus on $a_N$
    $\frac{\partial}{\partial a_N}E\left[\left(\theta-\sum^{N-1}_{n=0} a_nx[n]-a_N\right)^2\right]\\[0.2cm] =-2E\left[\theta-\sum^{N-1}_{n=0}a_nx[n]-a_N\right]=0\\[0.3cm] \rightarrow a_N=E(\theta)-\sum^{N-1}_{n=0}a_nE(x[n])$
  • Step 2 : Plug-In Step 1, Result for $a_N$
    $\text{Bmse}(\hat \theta)=E\left\{\left[\sum^{N-1}_{n=0}a_n(x[n]-E(x[n]))-(\theta-E(\theta))\right]^2\right\}$
    Let $\text{a}=[a_0\;a_1\;\cdots\;a_{N-1}]^T$
    $\text{Bmse}(\hat\theta)=E\left\{\left[a^T(\text{x}-E(\text{x}))-(\theta-E(\theta))\right]^2\right\} \\[0.2cm] =E\left[a^T(\text{x}-E(\text{x})(\text{x}-E(\text{x}))^Ta\right] - E\left[a^T(\text{x}-E(\text{x}))(\theta-E(\theta))\right]\\[0.2cm] -E\left[(\theta-E(\theta))(\text{x}-E(\text{x}))^Ta\right]+E\left[(\theta-E(\theta))^2\right]\\[0.2cm] =a^TC_{xx}a-a^TC_{x\theta}-C_{\theta x}a+C_{\theta\theta}=a^TC_{xx}a-2a^TC_{x\theta}+C_{\theta\theta}$
  • Step 3 : Minimize w.r.t. $\text{a}$
    $\frac{\partial\text{Bmse}(\hat\theta)}{\partial a}=2C_{xx}a-2C_{x\theta}=0\\[0.2cm] \rightarrow a=C^{-1}_{xx}C_{x\theta}$
  • Step 4 : Combine results
    $\hat \theta=a^T\text{x}+a_N=C^T_{x\theta}C^{-1}_{xx}\text{x}+E(\theta)-C^T_{x\theta}C^{-1}_{xx}E(\text{x})\\[0.2cm] \rightarrow\hat \theta=E(\theta)+C_{\theta x}C^{-1}_{xx}(\text{x}-E(\text{x)})$
  • Step 5 : Find Minimum Bmse
    $\text{Bmse}(\hat\theta)=C^T_{x\theta}C^{-1}_{xx}C_{xx}C^{-1}_{xx}C_{x\theta}-2C^T_{x\theta}C^{-1}_{xx}C_{x\theta}+C_{\theta\theta}\\[0.2cm] =C_{\theta\theta}-C_{\theta x}C^{-1}_{xx}C_{x\theta}$

Linear MMSE - Example

• DC Level in WGN with Uniform Prior PDF
  $x[n]=A+w[n],\;n=0,\;\cdots,N-1\\[0.2cm] A:\text{parameter to estimate }\sim U[-A_0,A_0],\;w[n]:\text{WGN}\sim\mathcal{N}(0,\sigma^2)$

  • MMSE cannot be obtained in closed form

  • LMMSE estimator

    $E(A)=0\rightarrow E(\text{x})=0\\[0.2cm] C_{xx}=E(\text{x}\text{x}^T)=E\left[(A1+\text{w})(A1+\text{w})^T\right]=E(A^2)11^T+\sigma^2I\\[0.2cm] C_{\theta x}=E(A\text{x}^T)=E[A(A1+\text{w})^T]=E(A^2)1^T\\[0.2cm] \hat A=C_{\theta x}C^{-1}_{xx}\text{x}=\sigma^2_A1^T(\sigma^2_A11^T+\sigma^2I)^{-1}\text{x}\\[0.2cm] =\frac{\sigma^2_A1^T}{\sigma^2}\times(I+\frac{\sigma^2_A}{\sigma^2}11^T)^{-1} x$

    By matrix inversion lemma

    $((A+BCD)^{-1}=A^{-1}-A^{-1}B(DA^{-1}B+C^{-1})^{-1}DA^{-1}$

    $\hat A=\frac{\sigma^2_A}{\sigma^2_A+\sigma^2/N}\bar x=\frac{A^2_0/3}{A^2_0/3+\sigma^2/N}\bar x$

---

• Closed form solution is available
• We don't need to know the PDF. Only the first and second moments are required
• Statistical independence between $A$ and $\text{w}$ is not required
  Then only need to be uncorrelated
• Required information for LMMSE estimation :
  $\left[\begin{matrix}E(\theta)\\E(\text{x})\end{matrix}\right],\; \left[\begin{matrix}C_{\theta\theta}&C_{\theta x}\\C_{x\theta}&C_{xx}\end{matrix}\right]$
• Note that LMMSE estimator is suboptimal due to the linearity constraint

---

Geometrical Interpretations

• Zero mean random variables $\theta'=\theta-E(\theta),\;\text{x}'=\text{x}-E(\text{x})$
• Find $\hat \theta=\sum^{N-1}_{n=0}a_nx[n]$ such that minimizes
  $\text{Bmse}(\hat \theta)=E\left[(\theta-\hat\theta)^2\right]$
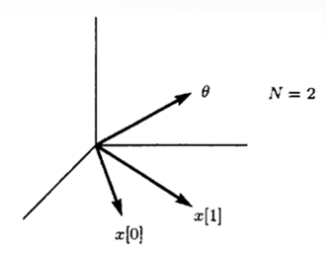
• Geometric analogy
  • $\theta,x[0],x[1],\dots,x[N-1]$ are elements in a vector space
  • Norm : $||x|| = \sqrt{E(x^2)}=\sqrt{\text{var}(x)}$
  • Inner product : $(x,y)=E(xy),(x,x)=E(x^2)=||x||^2$
  • $x$ and $y$ are orthogonal if $(x,y) = E(xy) =0$
    

---

• $\{a_n\}$ minimizes the MSE,
  $E\left[(\theta-\hat\theta)^2\right]=E\left[\left(\theta-\sum^{N-1}_{n=0}a_nx[n]\right)^2\right]=\left|\left|\theta-\sum^{N-1}_{n=0}a_nx[n]\right|\right|^2$
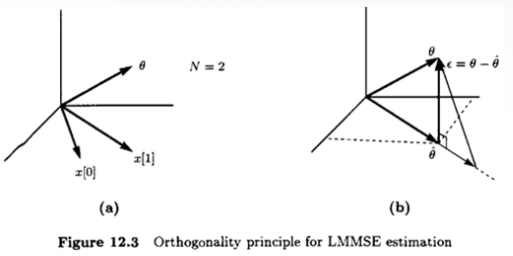
  • $\epsilon=\theta-\hat\theta$ should be orthogonal to the subspace spanned by $\{x[0],x[1],\cdots,x[N-1]\}$
  • $\epsilon \perp x[0], x[1], \dots, x[N-1]$
  • $E[(\theta-\hat \theta)x[n]] =0,\;n=0,1,\cdots,N-1$
    (Orthogonality principle or Projection theorem)
    $E \left[ \left( \theta - \sum_{m=0}^{N-1} a_m x[m] \right) x[n] \right] = 0, \quad n = 0, 1, \dots, N-1\\[0.2cm] \implies \sum_{m=0}^{N-1} a_m E(x[m] x[n]) = E(\theta x[n]), \quad n = 0, 1, \dots, N-1$
    
• In matrix form,
  $\begin{bmatrix} E(x^2[0]) & E(x[0]x[1]) & \cdots & E(x[0]x[N-1]) \\ E(x[1]x[0]) & E(x^2[1]) & \cdots & E(x[1]x[N-1]) \\ \vdots & \vdots & \ddots & \vdots \\ E(x[N-1]x[0]) & E(x[N-1]x[1]) & \cdots & E(x^2[N-1]) \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{N-1} \end{bmatrix} = \begin{bmatrix} E(\theta x[0]) \\ E(\theta x[1]) \\ \vdots \\ E(\theta x[N-1]) \end{bmatrix}\\[0.2cm] \rightarrow \mathbf{C}_{xx} \mathbf{a} = \mathbf{C}_{x\theta} \quad \text{so} \quad \mathbf{a} = \mathbf{C}_{xx}^{-1} \mathbf{C}_{x\theta}\\[0.2cm] \hat{\theta} = \mathbf{a}^T \mathbf{x} = \mathbf{C}_{x\theta}^T \mathbf{C}_{xx}^{-1} \mathbf{x}$
• Bmse
  $\text{Bmse}(\hat{\theta}) = \left\lVert \theta - \sum_{n=0}^{N-1} a_n x[n] \right\rVert^2 = \mathbb{E} \left[ \left( \theta - \sum_{n=0}^{N-1} a_n x[n] \right)^2 \right]\\[0.2cm] = \mathbb{E} \left[ \left( \theta - \sum_{n=0}^{N-1} a_n x[n] \right) \left( \theta - \sum_{m=0}^{N-1} a_m x[m] \right) \right]\\[0.2cm] = \mathbb{E}(\theta^2) - \sum_{n=0}^{N-1} a_n \mathbb{E}(x[n] \theta) - \sum_{m=0}^{N-1} a_m \mathbb{E}(\theta x[m]) + \sum_{n=0}^{N-1} \sum_{m=0}^{N-1} a_n a_m \mathbb{E}(x[n] x[m])\\[0.2cm] = C_{\theta\theta} - \mathbf{a}^T \mathbf{C}_{x\theta} = C_{\theta\theta} - \mathbf{C}_{x\theta}^T \mathbf{C}_{xx}^{-1} \mathbf{C}_{x\theta}= C_{\theta\theta} - C_{x\theta} \mathbf{C}_{xx}^{-1} C_{x\theta}$

---

Geometrical Interpretations - Examples

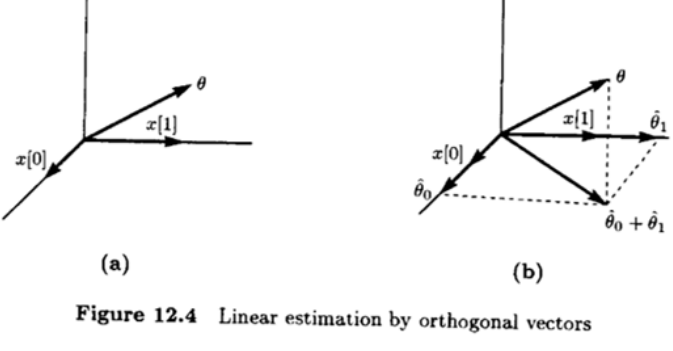
• Estimation by orthogonal vectors, where $x[0]$ and $x[1]$ are zero mean, uncorrelated
  $\hat{\theta} = \hat{\theta}_0 + \hat{\theta}_1\\[0.2cm] = \left( \theta, \frac{x[0]}{\|x[0]\|} \right) \frac{x[0]}{\|x[0]\|} + \left( \theta, \frac{x[1]}{\|x[1]\|} \right) \frac{x[1]}{\|x[1]\|}\\[0.2cm] = \frac{(\theta, x[0])}{(x[0], x[0])} x[0] + \frac{(\theta, x[1])}{(x[1], x[1])} x[1] \\[0.2cm] = \frac{\mathbb{E}(\theta x[0])}{\mathbb{E}(x^2[0])} x[0] + \frac{\mathbb{E}(\theta x[1])}{\mathbb{E}(x^2[1])} x[1]\\[0.2cm] = \begin{bmatrix} \mathbb{E}(\theta x[0]) & \mathbb{E}(\theta x[1]) \end{bmatrix} \begin{bmatrix} \mathbb{E}(x^2[0]) & 0 \\ 0 & \mathbb{E}(x^2[1]) \end{bmatrix}^{-1} \begin{bmatrix} x[0] \\ x[1] \end{bmatrix}= \mathbf{C}_{\theta x} \mathbf{C}_{xx}^{-1} \mathbf{x}$
  

---

Sequential LMMSE Estimation

• Increasing number of data samples for estimating fixed number of parameters
  • Data model :
    $\mathbf{x}[n-1] = \mathbf{H}[n-1]\boldsymbol{\theta} + \mathbf{w}[n-1]\\[0.2cm] \rightarrow \mathbf{x}[n] = \begin{bmatrix} \mathbf{x}[n-1] \\ x[n] \end{bmatrix} = \begin{bmatrix} \mathbf{H}[n-1] \\ \mathbf{h}^T[n] \end{bmatrix} \boldsymbol{\theta} + \begin{bmatrix} \mathbf{w}[n-1] \\ w[n] \end{bmatrix} = \mathbf{H}[n] \boldsymbol{\theta} + \mathbf{w}[n]$
  • Goal : Given an estimate $\hat\theta[n-1]$ based on $\text{x}[n-1]$, when new data sample $\text{x}[n]$ arrives, update the estimate to $\hat\theta[n]$

---

• Ex) DC level in WGN, with $\mu_A=0$
  • $\hat A[N-1]$ : LMMSE estimator for $A$ based on $x[0], x[1],\dots,x[N-1]$
    $\hat{A}[N-1] = \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2 / N} \bar{x}\\[0.2cm]\text{Bmse}(\hat{A}[N-1]) = \frac{\sigma^2}{N} \left( \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2 / N} \right) = \frac{\sigma^2 \sigma_A^2}{N \sigma_A^2 + \sigma^2}$
  • When $x[N]$ becomes available,
    $\hat{A}[N] = \frac{\sigma_A^2}{\sigma_A^2 + \frac{\sigma^2}{N+1}} \frac{1}{N+1} \sum_{n=0}^N x[n] = \frac{N \sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} \frac{1}{N} \left( \sum_{n=0}^{N-1} x[n] + x[N] \right)\\[0.2cm] = \frac{N \sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} \frac{\sigma^2_A+\frac{\sigma^2}{N}}{\sigma^2_A}\hat{A}[N-1] + \frac{\sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} x[N]\\[0.2cm] = \frac{N \sigma_A^2 + \sigma^2}{(N+1) \sigma_A^2 + \sigma^2} \hat{A}[N-1] + \frac{\sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} x[N]$

---

(correct the old estimate $\hat A[N-1]$ by a scaled prediction error)

• With gain or scaling factor $K[N]$
  $\hat{A}[N] = \hat{A}[N-1] + K[N] \left( x[N] - \hat{A}[N-1] \right)\\[0.2cm] K[N] = \frac{\sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} = \frac{1}{\frac{\sigma^2}{\text{Bmse}(\hat{A}[N-1])} + 1} =\frac{\text{Bmse}(\hat A[N-1])}{\text{Bmse}(\hat A[N-1])+\sigma^2} \quad \text{(decreases with } N\text{)}\\[0.2cm] \text{Bmse}(\hat{A}[N]) = \frac{\sigma^2 \sigma_A^2}{(N+1) \sigma_A^2 + \sigma^2} = \frac{N \sigma_A^2 + \sigma^2}{(N+1) \sigma_A^2 + \sigma^2} \text{Bmse}(\hat{A}[N-1])\\[0.2cm] = (1 - K[N]) \text{Bmse}(\hat{A}[N-1])$

---

S-LMMSE Estimation : Vector Space Approach

• Vector space approach
  • Given two observations $x[0],x[1]$ not orthogonal in general
  • We want to find $\hat{A}[1], \hat{A}[1] = \hat{A}[0] + \Delta \hat{A}[1], \Delta \hat{A}[1]$ is orthogonal to $\hat A[0]$
  • Let $\hat x[1|0]$ be the LMMSE estimator of $x[1]$ based on $x[0]$
    Then the error vector $\tilde{x}[1] = x[1] - \hat{x}[1|0] \perp x[0]$
  • Now we can think it as estimation based on orthogonal vectors $x[0]$ and $\tilde x[1]$
    $\rightarrow\;\Delta\hat A[1]$ becomes the LMMSE estimator of $A$ based on $\tilde x[1]$
  • $\hat \theta=C_{\theta x}C^{-1}_{xx}\text{x}$ for zero mean case
    $\hat{x}[1|0] = \frac{\mathbb{E}(x[0] x[1])}{\mathbb{E}(x^2[0])} x[0] = \frac{\mathbb{E}((A + w[0])(A + w[1]))}{\mathbb{E}((A + w[0])^2)} x[0] = \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2} x[0]$

---

• $\tilde x[1]=x[1]\perp\hat x[1|0]$ : new information from new sample : innovation
• The projection of $A$ along this vector is the desired correction :
  $\Delta \hat{A}[1] = \left( A, \frac{\tilde{x}[1]}{\|\tilde{x}[1]\|} \right) \frac{\tilde{x}[1]}{\|\tilde{x}[1]\|} = \frac{\mathbb{E}(A \tilde{x}[1])}{\mathbb{E}(\tilde{x}^2[1])} \tilde{x}[1],\;K[1]=\frac{E(A\tilde x[1])}{E(\tilde x^2[1])}\\[0.2cm] \hat{A}[1] = \hat{A}[0] + K[1] \left( x[1] - \hat{x}[1|0] \right)=\hat A[0]+K[1](x[1]-\hat A[0])\\[0.2cm] (\hat x[1|0]=\hat A[0]+\hat w[1|0]=\hat A[0])\\[0.2cm] \rightarrow \tilde x[1]=x[1] - \hat{x}[1|0] = x[1] - \hat{A}[0] = x[1] - \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2} x[0]\\[0.2cm] K[1] = \frac{\mathbb{E} \left[ A \left( x[1] - \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2} x[0] \right) \right]} {\mathbb{E} \left[ \left( x[1] - \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2} x[0] \right)^2 \right]} = \frac{\frac{\sigma_A^2 \sigma_A^2}{\sigma_A^2 + \sigma^2}}{\sigma_A^2 + \sigma^2 - \frac{2\sigma_A^4}{\sigma_A^2 + \sigma^2} + \left( \frac{\sigma_A^2}{\sigma_A^2 + \sigma^2} \right)^2 (\sigma_A^2 + \sigma^2)}\\[0.2cm] K[1] = \frac{\sigma_A^2 \sigma_A^2}{2\sigma_A^2 + \sigma^2}$
• Sequence of innovations $x[0],x[1]-\hat x[1|0],x[2]-\hat x[2|0,1],\cdots$ are obtained:
  Gram-Schmidt orthogonalization procedure
  $\hat{A}[N] = \sum_{n=0}^{N-1} K[n] \left( x[n] - \hat{x}[n|0, 1, \dots, n-1] \right)\\[0.2cm] K[n] = \frac{\mathbb{E}\left( A \left( x[n] - \hat{x}[n|0, 1, \dots, n-1] \right) \right)} {\mathbb{E}\left( \left( x[n] - \hat{x}[n|0, 1, \dots, n-1] \right)^2 \right)}$
• In sequential form,
  $\hat A[N]=\hat A[N-1]+K[N](x[N]-\hat x[N|0,1,\cdots,N-1])$
• Since $x[n]=A+w[n]$, where $A$ and $w[n]$ are uncorrelated,
  $\hat{x}[N | 0, 1, \dots, N-1] = \hat{A}[N | 0, 1, \dots, N-1] + w[N | 0, 1, \dots, N-1] = \hat{A}[N-1]\\[0.2cm] K[N] = \frac{\mathbb{E}\left( A \left( x[N] - \hat{A}[N-1] \right) \right)} {\mathbb{E}\left( \left( x[N] - \hat{A}[N-1] \right)^2 \right)}$

---

---

Winer Filtering

• Signal Model:
  $x[n] = s[n]+w[n]$
  • Problem Statement : Process $x[n]$ using a linear filter to probvide a de-noised version of the signal that has minimum MSE relative to the desired signal
    $\rightarrow$ Linear MMSE estimation problem

---

• Assuming that the data $x[0],x[1],\cdots,x[N-1]$ is WSS with zero mean, the $N\times N$ covariance matrix $C_{xx}$ is a symmetric Toeplitz matrix
  $\mathbf{C}_{xx} = \begin{bmatrix} r_{xx}[0] & r_{xx}[1] & \cdots & r_{xx}[N-1] \\ r_{xx}[1] & r_{xx}[0] & \cdots & r_{xx}[N-2] \\ \vdots & \vdots & \ddots & \vdots \\ r_{xx}[N-1] & r_{xx}[N-2] & \cdots & r_{xx}[0] \end{bmatrix} = \mathbf{R}_{xx}$
  $r_{xx}[k]$ is the ACF of $x[n]$ and $R_{xx}$ is the autocorr matrix. The parameter $\theta$ also zero mean

1. Filtering : estimate $\theta = s[n]$ based on $x[m]=s[m]+w[m],\;m=0,1,\cdots,n$
2. Smoothing : estimate $\theta = s[n],\;n=0,1,\cdots,N-1$ based on $x[0],x[1],\cdots,x[N-1]$ where $x[n]=s[n]+w[n]$
3. Prediction : estimate $\theta = x[N-1+l]\;(l>0)$ based on $x[0],x[1],\cdots,x[N-1]$

---

• General LMMSE estimation
  $\hat\theta=C_{\theta x}C^{-1}_{xx}\text{x}\\[0.2cm] M_{\hat \theta}=C_{\theta\theta}-C_{\theta x}C^{-1}_{xx}C_{x\theta}$
• Filtering problem : assuming signal and noise are uncorrelated,
  $\mathbf{C}_{xx} = \mathbf{R}_{ss} + \mathbf{R}_{ww}\\[0.2cm] \mathbf{C}_{\theta x} = \mathbb{E}(s[n] [x[0] \, x[1] \, \dots \, x[n]]) = \mathbb{E}(s[n] [s[0] \, s[1] \, \dots \, s[n]])\\ = [r_{ss}[n] \, r_{ss}[n-1] \, \dots \, r_{ss}[0]] := \mathbf{r}_{ss}^T\\[0.2cm] \rightarrow \hat{s}[n] = \mathbf{r}_{ss}^T (\mathbf{R}_{ss} + \mathbf{R}_{ww})^{-1} \mathbf{x}, \quad \mathbf{a} = (\mathbf{R}_{ss} + \mathbf{R}_{ww})^{-1} \mathbf{r}_{ss}$

---

• If we think it as a filter with impulse response $h[k],\;h[k]=a_{n-k}$
  $\hat{s}[n] = \sum_{k=0}^n a_k x[k] = \sum_{k=0}^n h[n-k] x[k] = \sum_{k=0}^n h[k] x[n-k]\\[0.2cm] (\mathbf{R}_{ss} + \mathbf{R}_{ww}) \mathbf{a} = \mathbf{r}_{ss} \quad \implies \quad (\mathbf{R}_{ss} + \mathbf{R}_{ww}) \mathbf{h} = \mathbf{r}_{ss}\\[0.2cm] \begin{bmatrix} r_{xx}[0] & r_{xx}[1] & \cdots & r_{xx}[n] \\ r_{xx}[1] & r_{xx}[0] & \cdots & r_{xx}[n-1] \\ \vdots & \vdots & \ddots & \vdots \\ r_{xx}[n] & r_{xx}[n-1] & \cdots & r_{xx}[0] \end{bmatrix} \begin{bmatrix} h[0] \\ h[1] \\ \vdots \\ h[n] \end{bmatrix} = \begin{bmatrix} r_{ss}[0] \\ r_{ss}[1] \\ \vdots \\ r_{ss}[n] \end{bmatrix}$
  Wiener-Hopf equations
  $\rightarrow \sum_{k=0}^n h[k] r_{xx}[l-k] = r_{ss}[l], \quad l = 0, 1, \dots, n\\[0.2cm] \text{As } n \to \infty, \quad \sum_{k=0}^\infty h[k] r_{xx}[l-k] = r_{ss}[l], \quad l = 0, 1, \dots\\[0.2cm] h[n] * r_{xx}[n] = r_{ss}[n] \quad \implies \quad H(f) = \frac{P_{ss}(f)}{P_{xx}(f)} = \frac{P_{ss}(f)}{P_{ss}(f) + P_{ww}(f)}$

  All Content has been written based on lecture of Prof. eui-seok.Hwang in GIST(Detection and Estimation)