1. Dimension reduction(차원 축소)
1.1 Vector transformation(벡터 변환)
https://youtu.be/g-Hb26agBFg
선형 변환은 임의의 두 벡터를 더하거나 스칼라 곱을 하는 것을 말한다. 두 벡터 공간 사이의 함수, 한 점을 한 벡터 공간에서 다른 벡터 공간으로 이동시키는데 그 이동규칙을 선형 변환이라고 한다.
f를 활용해서 임의의 두 벡터[x1, x2])에 대해서 [2x1+x2, x1-3x2]로 변환할 수 있다.
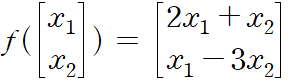
그렇기에 위의 f를 활용하는 것은 T를 곱해주는 것으로 이해할 수 있다.
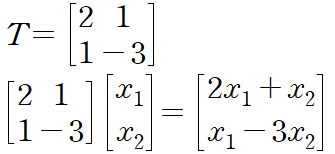
임의의 벡터를 다른 벡터로 변환하는 과정은 특정 T 매트릭스를 곱하는 것과 동일하다.
1.2 Eigenvector(고유벡터)
Transformation은 Matrix를 곱해 벡터(=데이터)를 다른 위치로 옮긴다는 뜻.
행렬 A를 선형 변환으로 위치를 옮겨 새롭게 볼 때에 선형 변환 A에 의한 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터
벡터를 변환할 때, 크기만 변화하고 방향은 변하지 않는 벡터
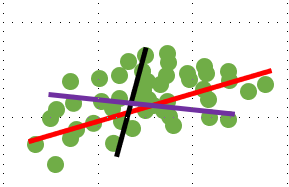
위의 그림에서 빨강, 보라, 검정 세 가지 선 중에서 초록색 데이터를 가장 잘 표현할 수 있는 선은 바로 빨간 선이다. 빨간 선을 저 초록 데이터의 고유 벡터로 이해하면 좋다.분산이 큰 vector를 선택해주어야 한다.
1.3 Eigenvalue(고유값)
고유벡터에서 상수배의 값.
변화한 크기의 값.
고유벡터와 고유값은 항상 쌍을 이루고 있다.
1.4 PCA(Principle Component Analysis, 데이터 차원 축소)
1.4.1 PCA는 뭘까?
주성분 분석이라고도 한다. 기존의 여러 변수를 재조합(Selection, Extraction)하여 고차원에서 저차원으로 차원을 축소해준다.
1.4.2 PCA를 해야하는 이유.
- 첫째: 1차원은 선(x축), 2차원은 면(x, y축), 3차원은 입체(x, y, z축)으로 표현할 수 있다. 그리고 우리가 이해할 수 있다. 그렇지만 4차원, 6차원, 10차원은??? 이해할 수 없다.
- 둘째: 데이터를 분석할 때 사용하는 feature가 모두 똑같은 비중으로 중요하지가 않다.
예를 들어 우리나라 경제를 분석할 때 여러 중요한 것 중에 하나는 수출입이다. 우리나라가 교역하는 국가 중에서 미국, 중국, 일본의 중요도와 남아프리카공화국, 적도기니, 팔라우와 같은 국가들이 분석에 차지하는 비중은 크게 차이날 수 밖에 없다. 그렇기에 전자의 경우는 한국의 경제 분석에 꼭 포함시켜야 하지만, 후자의 국가들은 제외하고 분석하여도 그 결과에 큰 차이가 나지 않을 것이다.
데이터를 분석할 때에도 이와 비슷한 이유로 중요한 feature는 포함시키고 나머지는 제외시키는 것이 중요하단 뜻! - 셋째: Overfitting(과적합)의 문제, 샘플(데이터)의 수에 비해 feature의 수가 너무 많은 경우 과적합의 문제가 발생한다. 과적합은 주어진 샘플은 너무나도 잘 설명하지만, 주어진 샘플을 제외하고 실제 데이터에서는 힘을 제대로 못 쓰는 경우를 의미한다.
아래의 그림과 같은 경우라고 이해하면 된다. 보라색은 분석에 사용한 데이터, 주황색은 새로운 실제 데이터. 회귀 분석을 진행하였을 때 주황색, 실제 데이터에도 적합해야 하지만 초록색 선은 전혀 반영하지 못하고 있다.
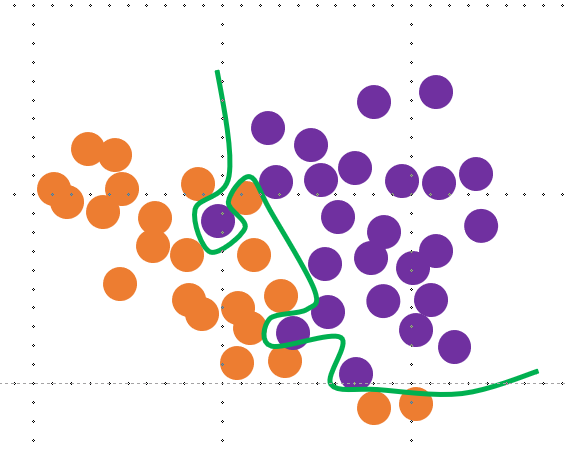
1.4.3 PCA는 어떻게 할까?
차원 축소에는 여러 방법이 있는데 여기서는 크게 Selection과 Extraction을 살펴본다.
Selection(선택): 왼쪽의 데이터는 x축에 size, y축에 rooms를 두어 2차원으로 표현했다. 하지만 오른쪽의 그래프는 x축 size만 남겨두어 1차원으로 축소했다. 이런 것이 pca, 데이터 차원 축소의 일종이다.
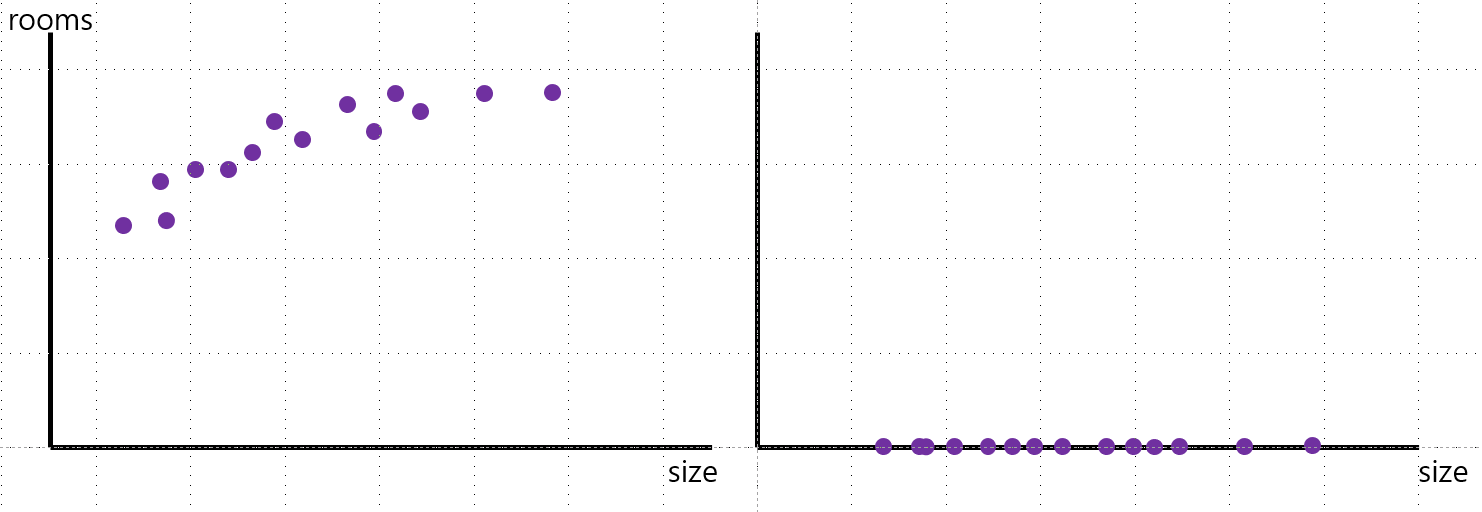
장점: 선택한 feature를 해석하기 쉽다.
단점: 선택하고 선택하지 않은 feature 사이의 연관성을 염두해두어야 한다.
예) LASSO, Genetic algorithm 등
Extraction(추출): 기존에 있는 feature와 그것을 활용해 새롭게 만든 feature를 사용하는 것. 마치 커피의 원두를 로스팅 하는 것과 비슷하다.
장점: feature 사이의 연관성이 고려된다. feature 수를 많이 줄일 수 있다.
단점: 그렇게 해서 나온 feature의 해석이 어렵다.
예) PCA, Auto-encoder 등
- 벡터를 바꾼다: 벡터의 방향을 바꾸거나(덧셈), 크기를 바꾸거나(곱셈)
2. Clustering
2.1 Scree plots
pca를 통해 차원을 축소한다고 했다. 그러면 축소를 하는데 얼마나 축소해야하나? 가 문제가 될 수 있다.
scree plot은 주성분을 x축에, 주성분의 Eigenvalue(고유값, 분산)을 y축에 두고 시각적으로 얼마나를 판단하게 도와준다.
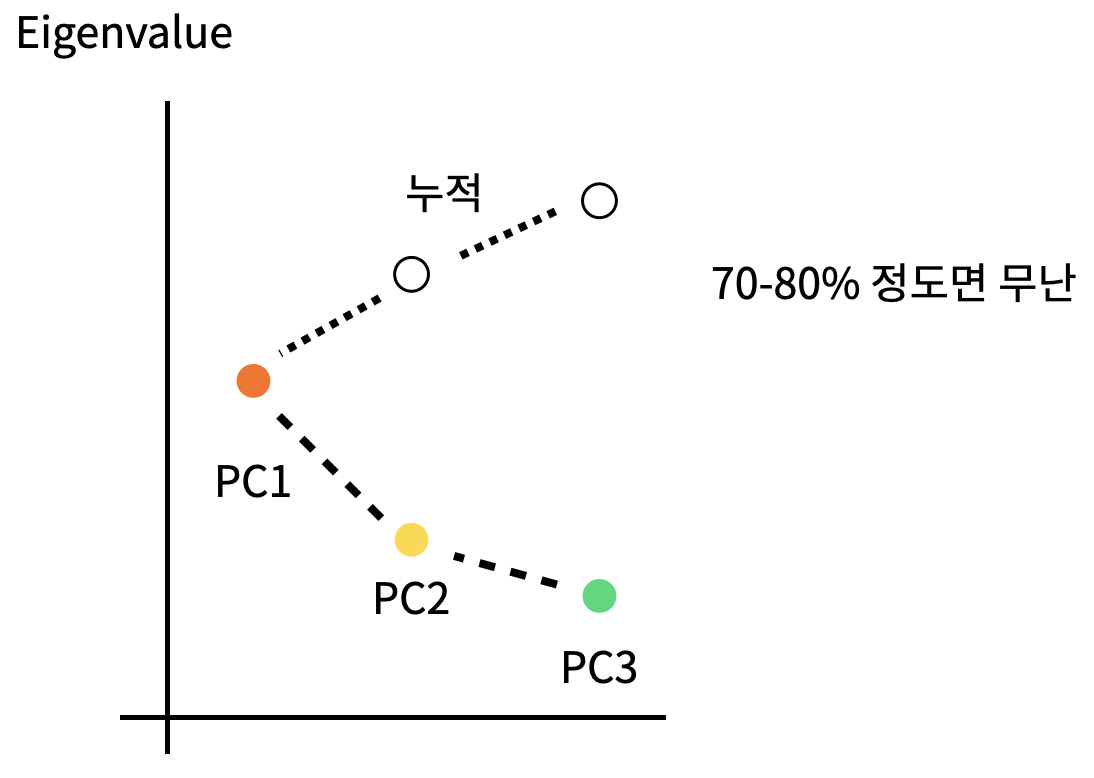
2.2 지도학습과 비지도학습
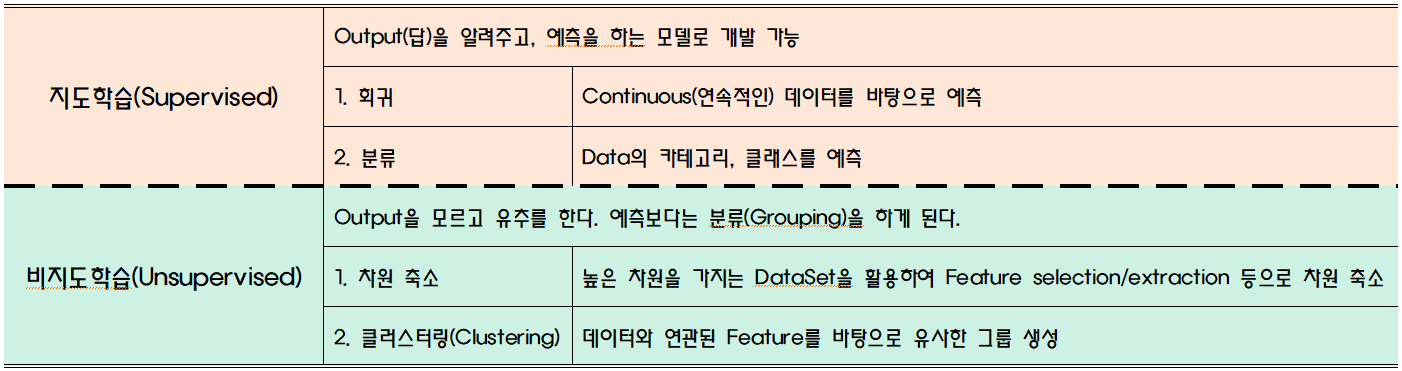
강화학습(Reinforcement): 머신러닝의 여러 유형 중 하나. 기계가 좋은 행동을 할 경우 보상, 그렇지 않을 경우 처벌
2.3 Clustering(클러스터링)
Unsupervised Learning의 한 종류
주어진 데이터들이 얼마나 그리고 어떻게 유사한지 알 수 있다.
하지만 정답을 보장하지 않기에 EDA를 위한 방법으로 많이 사용된다.
다만, 우리가 알 수 없는(혹은 몰랐던) 특성을 찾아내준다.
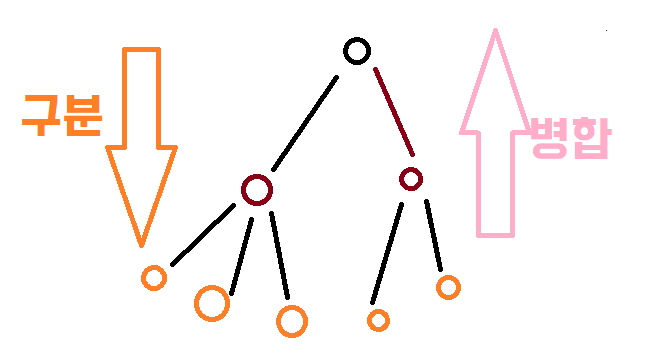
2.3.1 Hierarchical(계층, 위계)
Aggolomerative(병합): 개별 포인트에서 시작 후 점점 크게(위로) 합쳐간다.
Divisive(구분): 한개의 큰 클러스터에서 시작해서 점점 작게(아래로) 나뉘어져 간다.
2.3.2 K-means Clustering
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/ 실습해볼 수 있는 사이트
임의로 spot을 만들고 가장 가까운 것으로 Grouping 및 spot은 각각의 그룹의 중앙으로 이동한다.
과정: 1) k개의 랜덤한 데이터를 cluster의 중심점으로 설정. 2) 중심점 근처(가장 가까운 데이터)의 데이터를 해당 cluster로 할당한다. 3) 변경된 cluster에 대해 중심점을 새로 계산. 4)cluster에 유의미한 변화가 없을 때까지 2)~3)을 계속 반복
K를 결정하는 방법: 1)They Eyeball Method: 사람이 주관적으로 K를 판단 2)Metrics: 객관적인 지표를 설정하여 K를 결정
Elbow Method: k의 개수가 3일때 최적. L자 모양의 그래프가 사람의 팔꿈치와 닮았다고 해서 Elbow라고 부른다. 팔꿈치 모양의 k를 선택하면 된다.
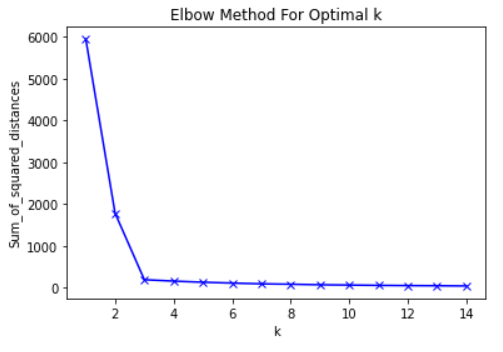
- K의 개수에 따라 달라지는 그룹
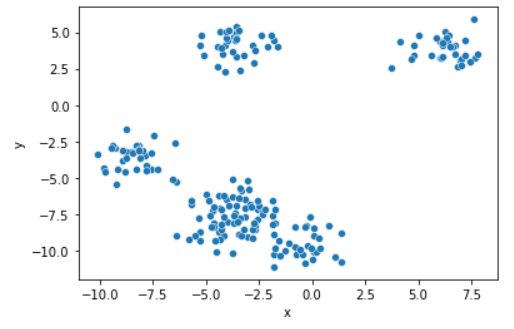
원본 scatter plot
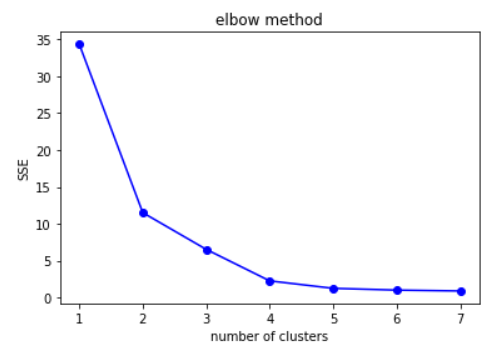
위 그래프를 보았을 때에는 4개가 좋아보인다.
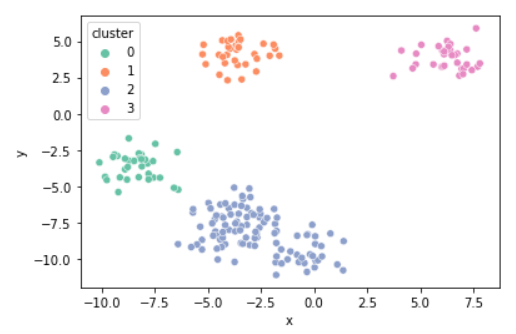
k = 4
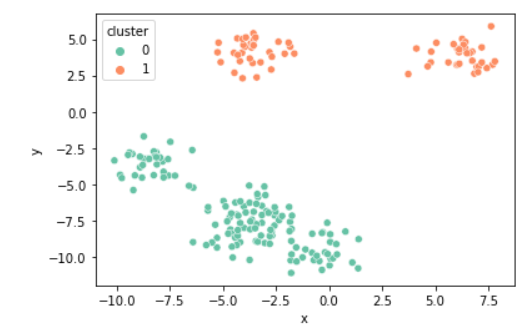
k = 2
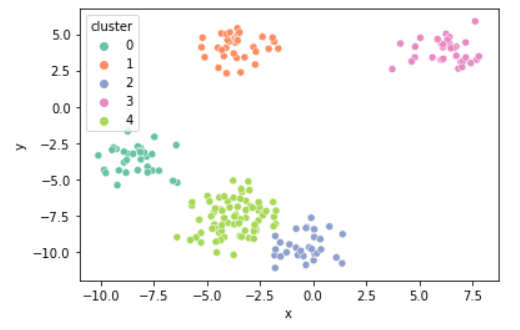
k = 5
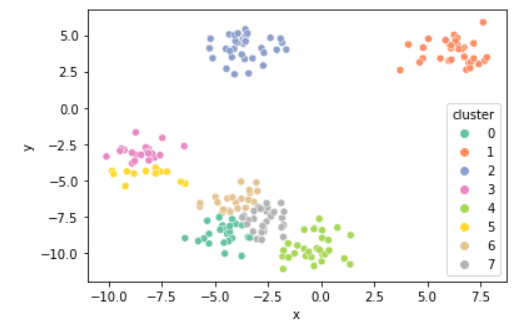
k = 8