📌 ML With Graphs
📄GNN(Graph Neural Networks)
이전에 변환식 노드 임베딩(Transductive Node Embedding) 에 대해 살펴봤지만, 여러 단점이 있었다. GNN 은 대표적인 귀납식 노드 임베딩(Inductive Node Embedding) 으로 임베딩 그 자체가 아닌 encoder를 생성하여 다음과 같은 장점을 가진다.
-
학습이 진행된 이후에 추가 정점에 대해서도 임베딩을 얻을 수 있다.
-
모든 정점에 대한 임베딩을 미리 계산하여 저장해둘 필요가 없다.
-
정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 있다. 이때 속성 정보는 지역,성별,연령,키워드에 대한 one-hot vecotor, 정점 중심성,군집계수 등이 될 수 있다.
✏️ 구조
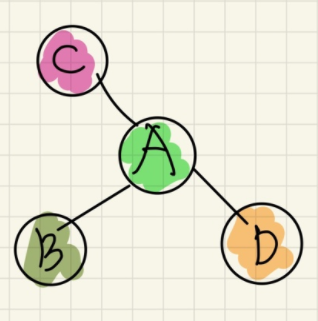
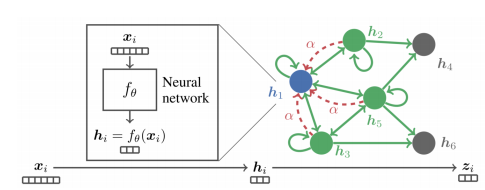
각 정점 의 속성(Attribute) 벡터 라고 했을때, 위와 같은 그래프가 주어졌다고 가정한다면, GNN의 구조는 다음과 같다.
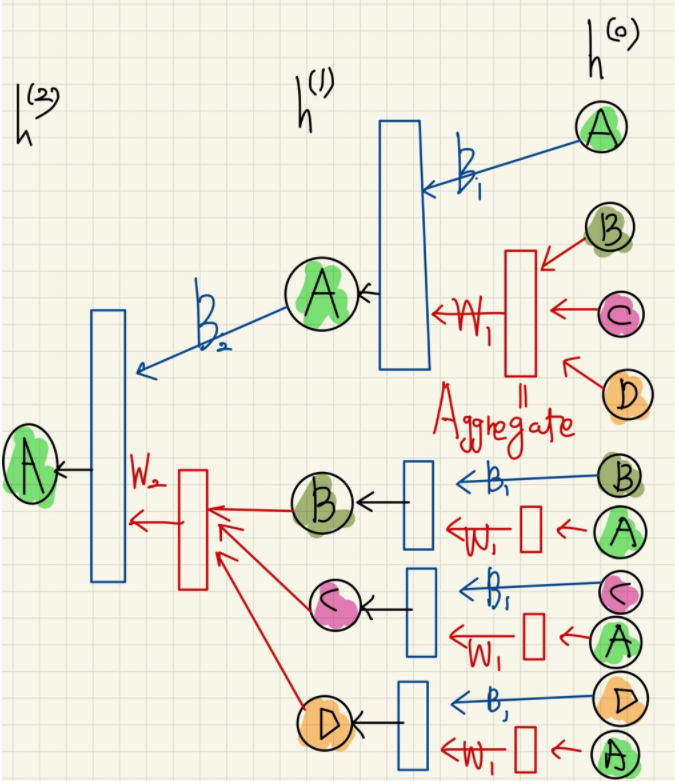
위의 구조에서 주목해야할 것은 aggregation 함수 와 이웃 노드들의 활용 이다. 각 layer 에서는 각 노드 임베딩을 위해 자신을 포함한 이웃 노드들을 입력으로 받는다. 이때 0번째 layer에서는 정점 v의 속성 벡터 를 입력으로 받는다. 이 후 입력노드들 중 자기자신의 제외한 이웃노드들의 임베딩은 aggregation 하여 노드 정보를 집계한다. aggregation 함수가 존재하는 이유는 각 노드마다 이웃하는 노드의 수가 달라질수 있으므로 aggregation 함수를 통해 이 문제를 해결한다. 그리고 자기 자신의 노드 의 임베딩과 함께 이웃노드들의 집계된 정보를 신경망에 적용하여 그 다음 layer의 의 임베딩을 얻는다. 위의 과정을 반복하여 마지막 층에서의 정점 의 임베딩 를 얻는다. 이를 수식으로 표현하면 다음과 같다.
✏️ 학습
학습의 전체적인 과정은 다음과 같다.
- 임베딩을 얻고자 하는 각 노드 별 computation graph 를 얻는다.

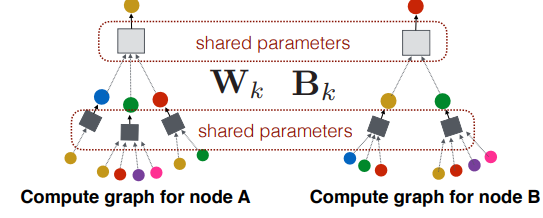
- backpropagation 을 통해 손실함수를 최소화 한다. 이때, 주목할 것은 서로 다른 대상 노드간에도 각 layer의 학습변수 와 는 공유(shared parameter) 된다는것이다.
그렇다면 손실함수는 어떻게 정의될 수 있을까? 노드임베딩 학습의 목표는 여러가지가 있을수 있겠지만, 이전 transductive node embedding 에서 살펴봤던 것처럼 정점간 거리를 보존하는것을 목표로 할 수 있다. 만약 간단하게 인접성을 기반으로 유사도를 정의한다고 가정하면, 인접행렬(Adjacency Matrix) 를 이용하여 다음과 같이 정의할 수 있을 것이다.
또한 downstream task의 손실함수 를 이용하여 end-to-end 학습도 가능하다. 가령, 최종 학습 목표가 node embedding이 아닌 node가 사람인지 기계인지 분류하는 node classification 이라고 가정한다면 다음과 같이 cross entropy function 을 전체 프로세스의 손실함수로 사용하여 end-to-end 학습을 할 수 있다.

일반적으로 그래프의 end-to-end 학습을 통한 분류는 transductive node embedding 이후 별도의 분류기를 사용하는 것 보다 정확도가 높다고 알려져 있다.
✏️ 활용
GNN의 각 layer의 학습변수 ,는 shared parameter 이기 때문에 학습된 신경망을 적용하여 학습에 사용되지 않은 정점의 임베딩을 얻을 수 있다.

- 학습 이후에 추가된 정점의 임베딩을 얻을 수 있다.
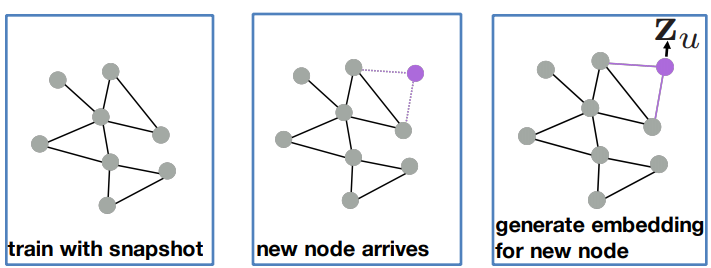
- 새로운 그래프에 적용할 수 있다.

📄GCN(Graph Convolutional Networks)

GCN 의 가장 기본적인 아이디어는 CNN에서 픽셀 대상으로 하던 합성곱(convolution) 연산 개념을 그래프에 적용하는 것 이다. CNN에서는 kernel(shared parameter) 이 이동하면서 local feature 들이랑만 연산하고 feature map을 생성하므로 feature map의 각각의 값은 local feature 들에 의해서만 학습된다. 즉 많은 중복 feature들이 동일한 가중치와 연산하기 때문에 feature map 의 각각의 값 은 근처에 있는 값끼리 상관관계가 높아진다. 따라서 CNN은 근처 data 끼리 상관관계가 높은 input data에 대해 학습이 더 잘 이루어진다. 그렇다면 이 특징들을 어떻게 GCN에 적용시킬수 있을까?
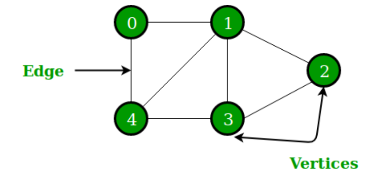
- 먼저 graph를 표현하기위해 adjacency matrix 와 feature matrix(attribute matrix) 를 구성한다. 이때 주목할것은 인접 행렬은 자기 자신으로 가는 edge가 없다면 대각 원소(diagonal elements)를 0으로 채우지만
GCN에서는 자기 자신의 정보를 이용하기 위하여 1로 채워 준다.
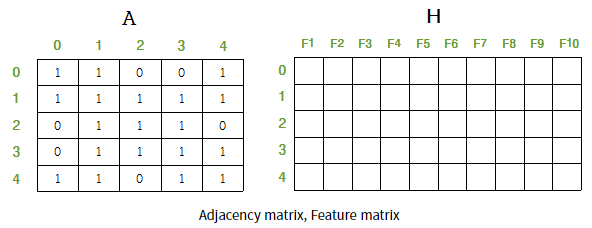
GNN과는 다르게 aggregation 함수에선 학습변수를 하나로 공유 하고 정규화 방법 을 변화시켰다.

위의 aggregation 함수를 일반화 한다면 다음과 같다.
와 |feature|x|kernel size| 크기의 의 곱 matrix에서 번째 ccolumn 은 모든 H state들에 번째 weight kernel(shared parameter)를 곱했을때 나온 값들이다.
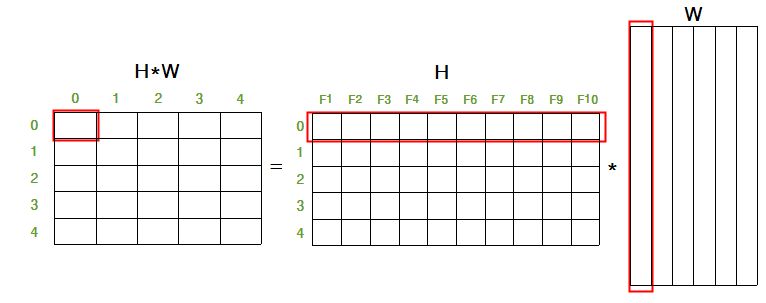
이때, 는 각 노드의 인접 노드 정보를 가지고 있으므로 를 에 곱하여 각 노드의 인접한 state만 더한 값으로 업데이트 한다.
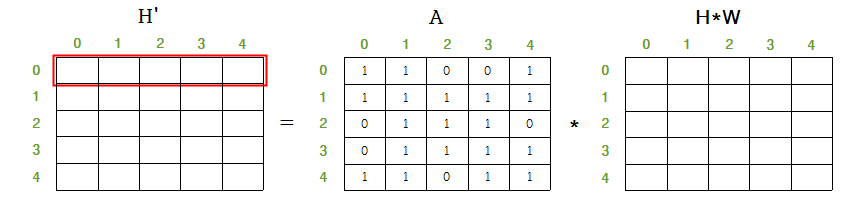
하지만 아직 정규화(normalization) 과정이 표현되지 않았는데, 정규화 과정을 포함한 일반화 는 다음과 같다.
는 diagonal node degree matrix 로 인접행렬 의 각 row를 더하면 얻을 수 있는데, 를 의 앞뒤에 곱해줌으로써 정규화된 matrix를 얻을 수 있다. 이때 는 가 diagonal matrix 이므로 역행렬은 각 성분원소의 역수이고 거기에 제곱한 값을 가짐을 알 수 있다.
✏️ GraphSAGE
GCN의 발전된 형태인 GraphSAGE 에서 주목할 것은 aggregation 함수이다.
위와 같이 이전 층 자신의 embedding 를 concatenation 한다. 이때 함수는 다음과 같이 여러 방법으로 수행할 수 있다.

이때, pooling aggregation에서 element-wise mean/max 는 행렬 이 있다고 가정하였을때, 각 column에 대해 mean/max 를 적용하는 것을 말하며 결과적으로 의 vector를 얻는다.
📄 CNN vs GNN

CNN 과 GNN의 공통점은 이웃의 정보를 aggregation을 반복한다는 것이다. 그렇다면 그래프의 인접행렬에 CNN을 적용할수 있는것이 아닐까?
결론부터 말하자면 적용할수는 있으나 효과적이지 않다. 가장 큰 이유는 두가지로 생각해볼수 있는데,
-
CNN에서는 이웃의 수가 균일하지만GNN에서는 그렇지 않다. -
CNN이 주로 쓰이는 이미지에서는 인접 픽셀이 유용한 정보를 담고 있을 가능성이 높지만, 그래프의 인접 행렬에서의 인접 원소는 제한된 정보를 가진다. 또한 인접 행렬의 행과 열의 순서는 임의로 결정되므로 인접 원소간의 유용한 정보를 담지 않을 수 있다.
📄GAT(Graph Attention Networks)
기존의 GNN/GCN에서는 이웃들의 정보를 동일한 가중치 / 단순히 연결성을 고려한 가중치 로 평균을 낸다. 하지만 실제 그래프에서는 이웃별로 미치는 영향이 다를 수 있기 때문에 단순하게 이웃들의 정보를 동일한 가중치로 평균을 내는 것은 문제가 있다.
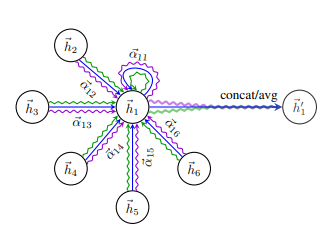
GAT 는 이것을 보완하기 위해 self-attention 을 활용하여 각 층에서 이웃 노드 j 에서 정점 i로의 가중치 자체도
학습한다.

-
해당 층의 노드 의 임베딩 에 신경망 를 곱해 새로운 임베딩 을 얻는다.
-
노드 , 의 새로운 임베딩 , 를 concatenation 후
attention coefficients를 내적한다. 이때, 는 모든 노드가 공유하는 학습변수이다. -
2의 결과에
softmax를 적용한다.
그리고 하나의 attention 이 아닌 여러 개의 attention(Multi-head Attention) 을 학습한 뒤 결과를 concatenation 하여 사용한다.
📄 Graph Embedding
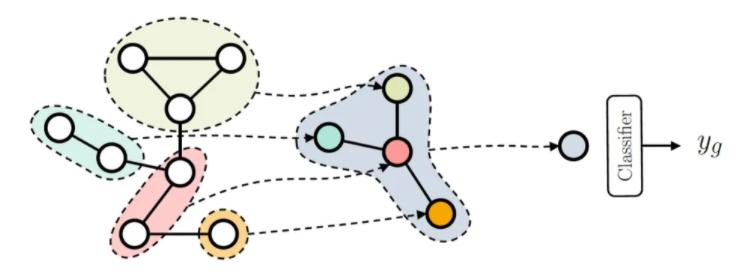
이전에 살펴본 Node Embedding은 개별 정점을 백터의 형태로 표현하는 반면 Graph Embedding 은 그래프 전체를 벡터의 형태로 표현한다. 가령 그래프 형태로 표현된 화합물의 분자 구조로부터 특성을 예측하는 그래프 분류 등에 활용된다. 그리고 Graph Embedding 의 경우 그래프의 구조를 고려하므로 그래프 분류 등 downstream task 에서 더 높은 성능을 얻는것으로 알려져 있다.
Graph Embedding 을 얻기 위해 Graph Pooling 을 사용할 수 있는데, 이는 노드 임베딩들로부터 그래프 임베딩을 얻는다.
📄 Over-smoothing
Over-smoothing 이란 그래프 신경망의 layer 가 증가하면서 정점의 임베딩이 서로 유사해지는 현상을 말한다. 쉽게 생각해보면 layer가 늘어나면 그래프의 지역적 정보만이 아닌 전체 정보를 학습하게 되어 유사하게 임베딩 되는것을 알 수 있다. 또한 이는 Small World Effect와 관련이 있는데, 적은 수의 층으로도 다수의 정점에 의해 영향을 받게 된다.

Over-smoothing은 downstream task에서 정확도가 감소하게 만든다. 그래서 이를 해결하기 위해 residual 을 추가하였지만 결과는 미미했다.
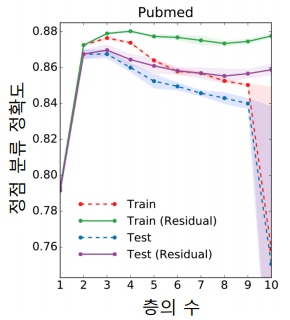
위의 결과를 보면 알 수 있듯이 layer가 2~3 개 일때 정확도가 높은것을 확인할 수 있다. 그렇다면 이 문제를 해결하기 위해 다른 방법들은 무엇이 있을까?
- Jumping Knowledge Network : 마지막 layer의 임베딩 뿐만 아니라, 모든 layer의 임베딩을 함께 사용한다.

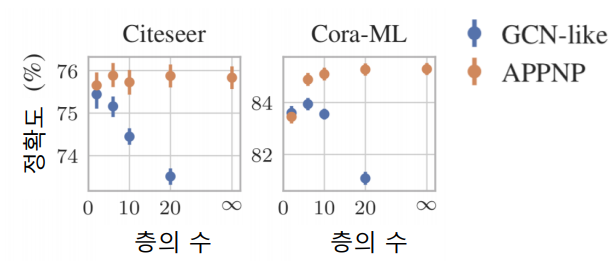
- APPNP : 0번째 layer를 제외하고는 신경망 없이 aggregation 함수를 단순화 한다. 아래의 결과를 보면 layer 증가에 따른 정확도 감소효과가 없는 것을 확인 할 수 있다.
📄 Data Augmentation
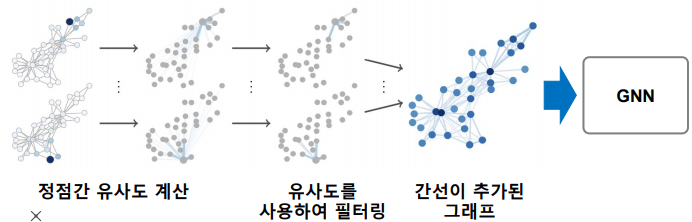
Data Augmentation은 다양한 기계학습 문제에서 효과적이다. 가령, 이미지 학습에서의 data augmentation 처럼 그래프 또한 data augmentation을 적용할 수 있다. 그래프에도 누락되거나 부정확한 간선이 존재할 수 있는데, random walk를 통해 정점간 유사도를 계산하여 유사도가 높은 정점 간의 간선을 추가하는 방법으로 data augmentation 한다.
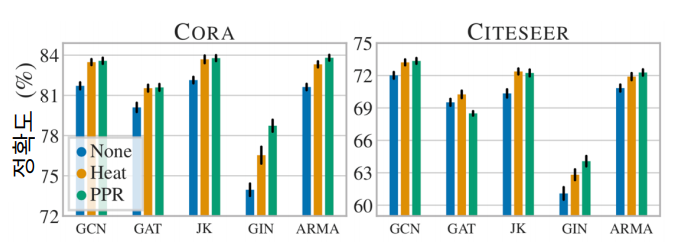
위를 보면 Heat ,PPR 방식의 augmentation을 한 결과 node classification 의 정확도가 개선되는 것을 확인할 수 있다.
