[ 유사 화장품 추천 프로젝트 ] 06. 역수 벡터화 & PCA

강현태·2022년 7월 14일
DS schooldatascienceprojectzerobase
0

유사 화장품 추천 프로젝트

목록 보기
7/8

유사 화장품 추천 프로젝트

역수 벡터화 & PCA 💬🔢📊

📝 목차

  1. 역수 벡터화
    1-1. 역수 벡터화 방법
    1-2. 기대효과
    1-3. 역수 벡터 매트릭스
  2. PCA
    2-1. PCA란?
    2-2. n_components 결정
    2-3. 최종 매트릭스

1. 역수 벡터화

1-1. 역수 벡터화 방법

기존 Count-Based 에서는

  • 성분이 함유되었으면 1
  • 성분이 함유되지 않았으면 0

으로 단순히 이진화하였음.

이번 역수 벡터화에서는 성분이 나열된 순서에 따라 값을 부여한 후
이를 역수로 변환하여 값을 부여

(테스트에 지속적으로 사용하고 있는 Joah-skin사의 peel-off mask)
예를 들어 해당 제품의 Caprylyl Glycol은 11번째에 나열되어 있다.
따라서 Caprylyl Glycol에 11이라는 값을 부여하여 다시 역수를 취한다. 1/11


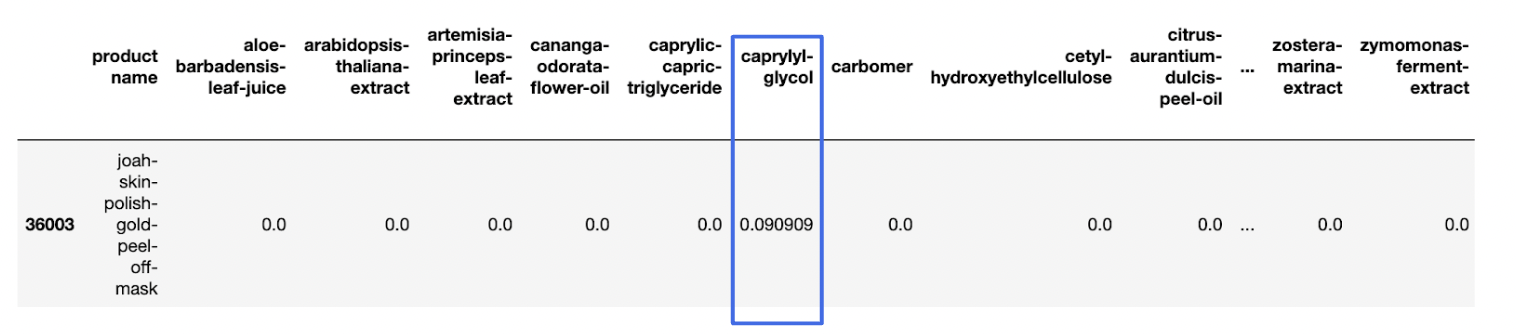
실제 벡터화하여 데이터프레임으로 만들면 위와 같다.


1-2. 기대효과

화장품의 성분은 함유량에 따라 내림차순 정렬되어 나열된다.
다시 말해, 많이 함유된 성분일수록 먼저 나타난다.
즉, 먼저 등장할수록 화장품에서 차지하는 비중이 높은 성분임.

따라서 순서대로 값을 부여한 후 역수로 취하면?
성분 나열순서에 따라 가중치를 부여할 수 있다.


1-3. 역수 벡터 매트릭스

데이터 형태는 Value로 Dictionary를 가진 Dictionary이다.
1. Key(제품명): Value(Ingredient Dictionary)
2. Value = Key(Ingredient Dictionary): Value(Ingredient, Vector)

from collections import defaultdict
ingredeint_dict = defaultdict(int)
ingredeint_name = list(unique_ingredient['formatted ingredients'])
for name in ingredeint_name:
    ingredeint_dict[name] = 0

먼저 Value의 Value가 될 Dictionary를 초기화
Key(성분명) : Value(벡터, 현재는 0으로 초기화)

inverse_dict = defaultdict(int)
# for idx, row in tqdm_notebook(product.iloc[:7000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[7000:14000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[14000:21000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[21000:28000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[28000:35000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[35000:42000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[42000:49000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[49000:56000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[56000:63000,:].iterrows()):
# for idx, row in tqdm_notebook(product.iloc[63000:70000,:].iterrows()):
for idx, row in tqdm_notebook(product.iloc[70000:,:].iterrows()):
    inverse_dict[row['product name']] = ingredeint_dict.copy()
    for num, ing in enumerate(row['formatted ingredients'].split(',')):
        ing = ing.replace('[',',').replace(']','').replace("\'",'').replace(',','').strip()
        inverse_dict[row['product name']][ing] = 1/(num+1)

📌 코드 부연 설명

  • 77,000개 제품을 한 번에 진행하다보니 .. 메모리 부족으로 다운되어버림
  • 77,000개를 10번에 나눠서 작업 진행
  • 최종 데이터는 Inverse_dict
  • Key값은 제품명, Value값은 성분 Value의 Value는 벡터
inverse_matrix = pd.DataFrame(inverse_dict).T
# inverse_matrix.to_csv('inverse_matrix_0_7000.csv')
# inverse_matrix.to_csv('inverse_matrix_7000_14000.csv')
# inverse_matrix.to_csv('inverse_matrix_14000_21000.csv')
# inverse_matrix.to_csv('inverse_matrix_21000_28000.csv')
# inverse_matrix.to_csv('inverse_matrix_28000_35000.csv')
# inverse_matrix.to_csv('inverse_matrix_35000_42000.csv')
# inverse_matrix.to_csv('inverse_matrix_42000_49000.csv')
# inverse_matrix.to_csv('inverse_matrix_49000_56000.csv')
# inverse_matrix.to_csv('inverse_matrix_56000_63000.csv')
# inverse_matrix.to_csv('inverse_matrix_63000_70000.csv')
inverse_matrix.to_csv('inverse_matrix_70000_77000.csv')

이후에 데이터프레임으로 바꿔주고 11개의 csv file을 만들었다.

inverse_matrix = pd.concat([mat1,mat2,mat3,mat4,mat5,mat6,mat7,mat8,mat9,mat10,mat11]).reset_index().iloc[:,1:]
inverse_matrix.rename(columns={'Unnamed: 0':'product name'}, inplace=True)
inverse_matrix

11개의 csv 파일을 각각 mat#으로 할당해준 후 concat 하면 최종 데이터프레임 완성.
아래와 같다.

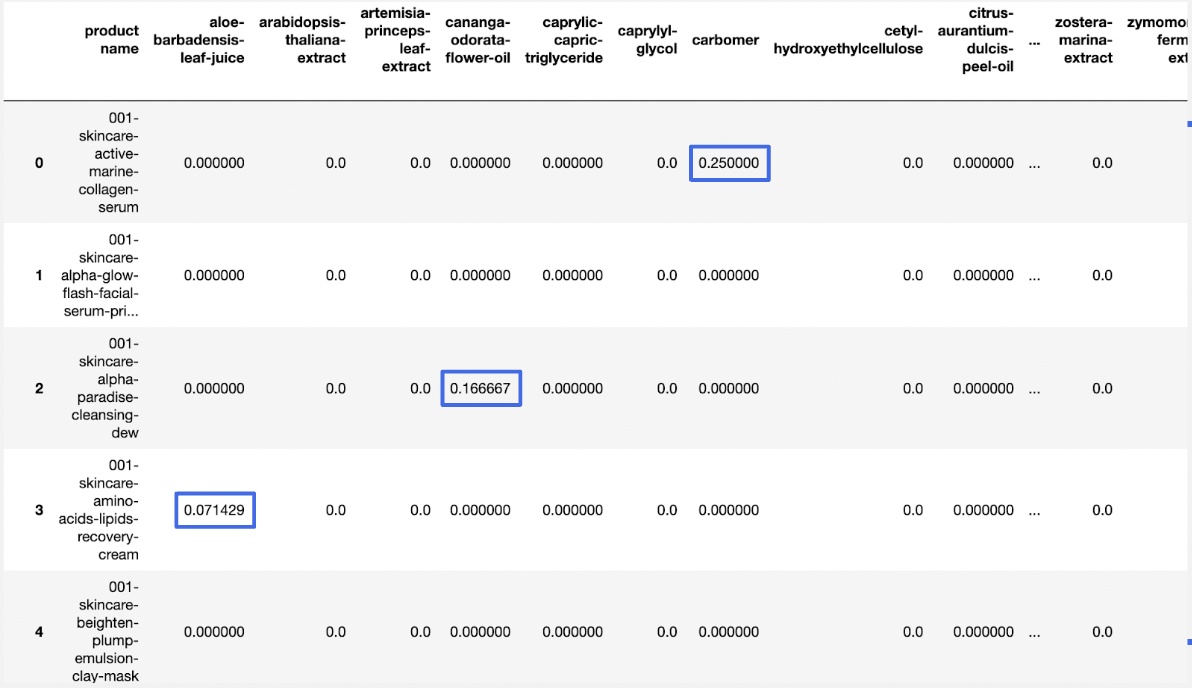
77,000 X 15,187 size의 데이터프레임이 완성됐다.
용량이 무려 5gb에 육박한다 ..


2. PCA

2-1. PCA란?

PCA는 차원축소의 방법 중 하나이다.

  • 차원축소
    : 일반적으로 차원이 증가할수록 데이터 좌표 간의 거리가 급속도로 멀어진다. 이를 희소(Sparse)한 구조를 가지게 된다고 표현하며, feature가 많을 수록 고차원에서 설명력과 신뢰도가 떨어진다. 이렇듯 매우 많은 다차원의 feature를 차원 축소해 feature 수를 줄이면 더 직관적으로 데이터를 이해할 수 있게 된다. 그리고 이 차원 축소의 방법에는 feature선택과 feature추출이 있으며, PCA는 feature 추출의 한 방법이다.

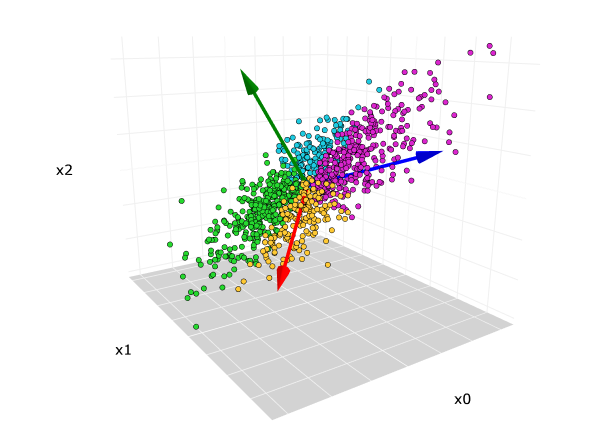
PCA를 간단하게 말하자면,
모든 성분을 압축하여 설명력이 높은 저차원의 소수의 feature를 새롭게 추출하는 것이다.

데이터에 대해 가장 높은 설명력을 지닌(Variance가 높은) 축을 찾아, 그 축을 중심으로 데이터를 새롭게 투영하는 것이다. 이것이 첫 번째 주성분(PCA)다.

두 번째 PCA는 첫 번째 축에 직교하는 직교벡터, 그 다음 PCA는 앞선 축에 직교하는 직교벡터 ... 식으로 진행된다.


2-2. n_components 결정


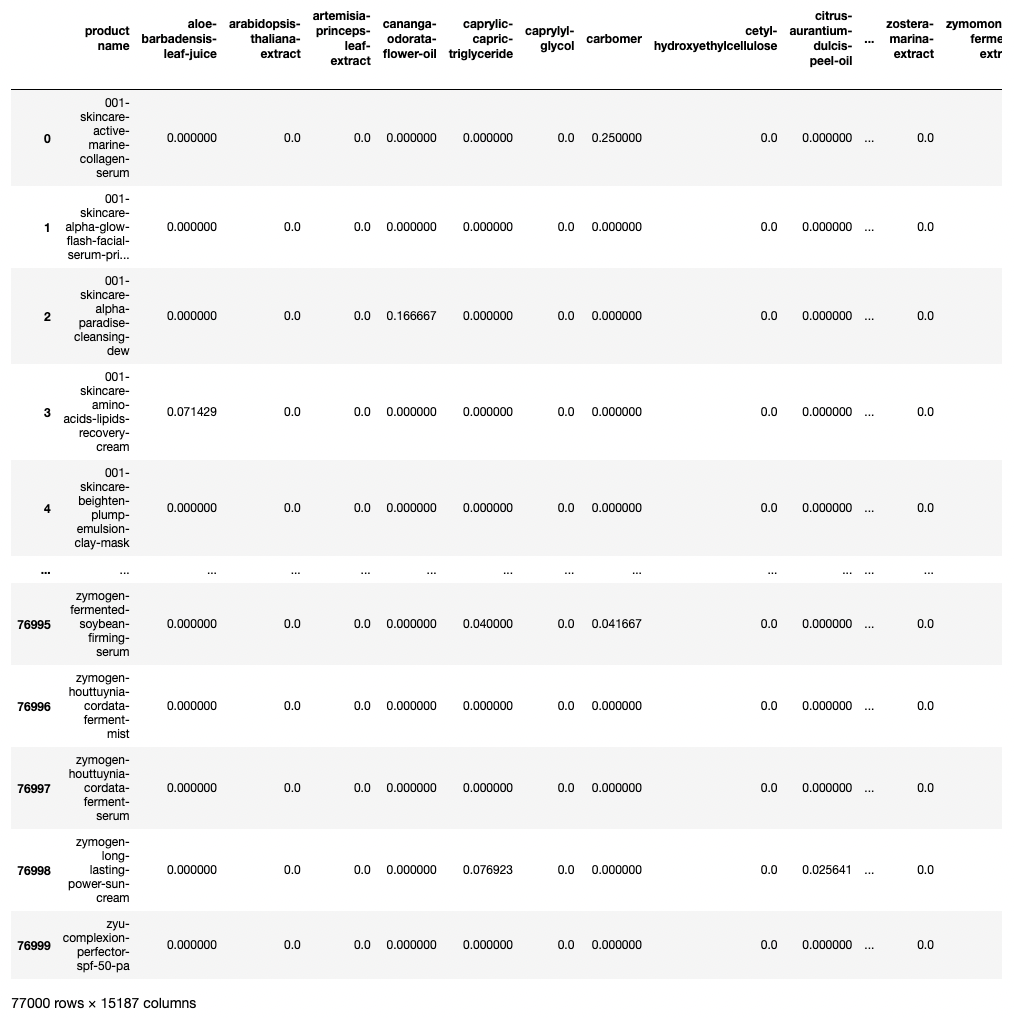
위에서 만든 Inverse_matrix의 차원을 축소해보자.

from sklearn.decomposition import PCA

def get_pca_data(data,n_components):
    pca = PCA(n_components=n_components)
    pca.fit(data)

    return pca.transform(data), pca
    
def get_pca_df(pca_data,pca):
    cols = ['pca_'+str(1+i) for i in range(pca.components_.shape[0])] 
    
    return pd.DataFrame(pca_data,columns=cols)

sklearn에 PCA가 내장되어 있다.
몇 개의 차원으로 축소할지 n_components를 결정하고,
fit 후에 transform 해주면 된다.

PCA로 차원축소한 데이터를 데이터프레임으로 만드는 함수까지 미리 만들었다.

import numpy as np
import matplotlib.pyplot as plt

skca_pca250,pca250 = get_pca_data(data,250)
print(np.sum(pca250.explained_variance_ratio_))

0.8024769096360096

먼저 250차원으로 줄인 데이터를 생성했다.
.explained_variance_ratio 함수를 통해 설명력을 확인할 수 있다.
250 차원에서 80% 설명력을 보임을 확인했다.

fig, ax = plt.subplots(figsize=(20,10))
#fig.figure(figsize=(15,15))
xi = np.arange(1, 251, step=1)
y = np.cumsum(pca250.explained_variance_ratio_)

plt.ylim(0.0,1.1)
if np.cumsum == 0.6:
    plt.plot(xi, y, marker='o', linestyle='--', color='r')
else:
    plt.plot(xi, y, linestyle='--',color='b')

plt.xlabel('Number of Components')
plt.xticks(np.arange(0,251, step=5),rotation=45) 
plt.ylabel('Cumulative variance (%)')
plt.title('The number of components required to explain variance')

plt.axhline(y=0.60, color='g', linestyle='-')
plt.text(0.5, 0.55, '60% threshold', color = 'green', fontsize=16)

plt.axhline(y=0.80, color='r', linestyle='-')
plt.text(0.5, 0.75, '80% cut-off threshold', color = 'red', fontsize=16)

ax.grid(axis='x')
ax.get_xticklabels()[11].set_color("green")
ax.get_xticklabels()[12].set_color("green")
ax.get_xticklabels()[49].set_color("red")

plt.show()
plt.show()
print(f'80% cut-off threshold: 245 components, explained variance {np.sum(pca250.explained_variance_ratio_[:245])}')
print(f'80% cut-off threshold: 57 components, explained variance {np.sum(pca250.explained_variance_ratio_[:57])}')

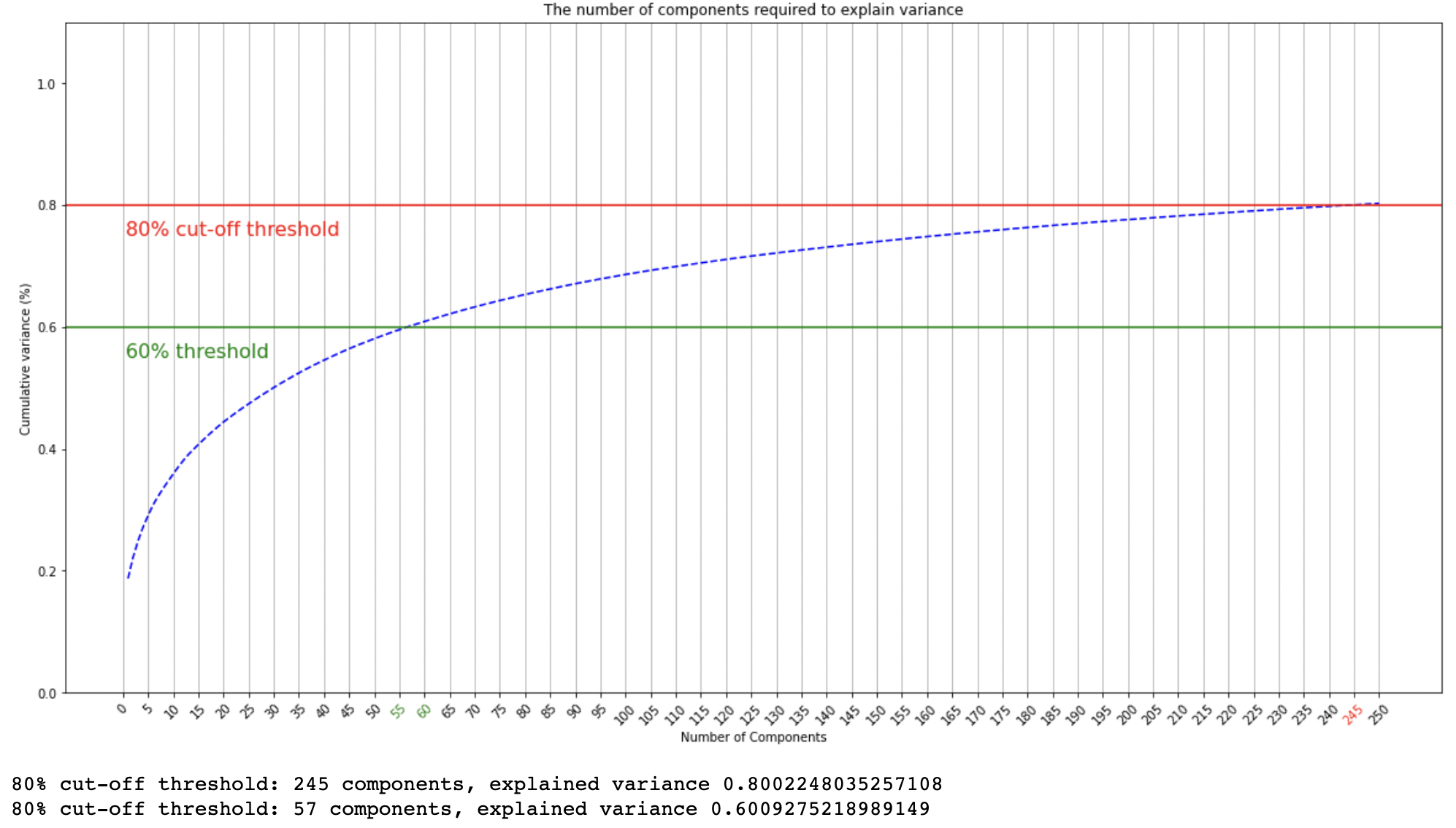
그래프로도 확인해보자.
x축은 주성분 개수, y축은 설명력이다.
파란색 곡선은 주성분 개수별 설명력
초록색 직선은 60% 설명력을 보이는 구간
빨간색 직선은 80% 설명력을 보이는 구간이다.

PCA245차원에서 80% 설명력을 보임을 확인하여, 245개의 주성분을 추출했다.

pca250_df = pd.DataFrame(prod)
pca250_df.rename(columns={'product name':'product'},inplace=True)
df = get_pca_df(skca_pca250,pca250)
df['product'] = prod
pca250_df = pd.merge(pca250_df,df,on='product')

먼저 250차원의 데이터 프레임을 만들고

pca245_df = pca250_df.copy(deep=True)
for i in range(50,45,-1):
    del pca245_df[f'pca_2{str(i)}']
    
pca245_df

250차원 데이터프레임을 카피하여 뒤의 다섯 차원을 제거했다.
최종적으로 245차원의 데이터 프레임 완성!

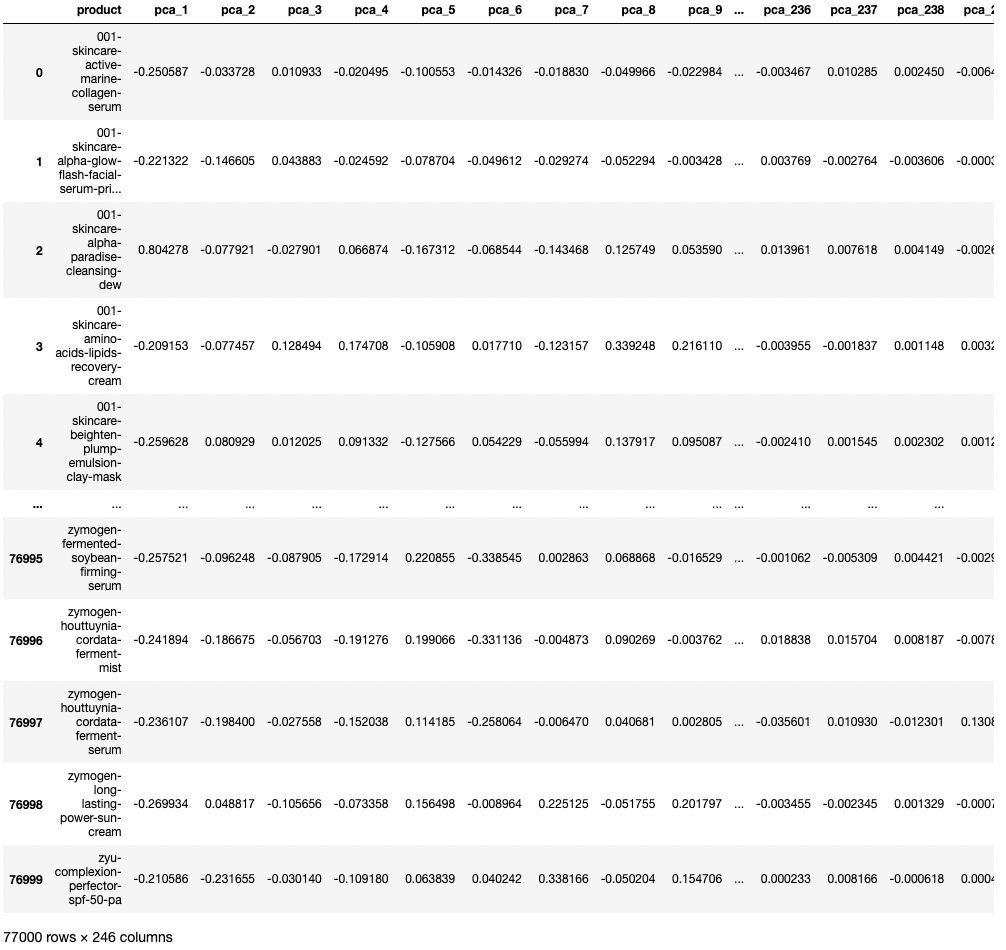
77,000 X 245 size의 데이터프레임이 완성됐다.

  • 성분순서를 고려하기 위하여 역수로 벡터화
  • 희소행렬 문제를 해소하기 위해 245차원으로 축소

이제 마지막으로 유사도 측정을 해보자.

profile
강현태
데이터 분석, ML/DL, 통계 지식을 공부하고 저장하는 공간
이전 포스트

[ 유사 화장품 추천 프로젝트 ] 05. 자카드 계수

다음 포스트

[ 유사 화장품 추천 프로젝트 ] 07. 유사도 측정 ver.2

0개의 댓글