Decision Tree

김혜성·2021년 2월 17일

Machine Learning

목록 보기

3/10

Decision Tree의 정의

Decision Tree(결정 트리)는 의사결정 트리라고도 하며, 분류(Classification)과 회귀(Regression) 모두 가능한 지도 학습 모델이다. 특정 기준이나 질문에 따라 데이터를 구분하는 모델을 결정 트리 모델이라고 한다.

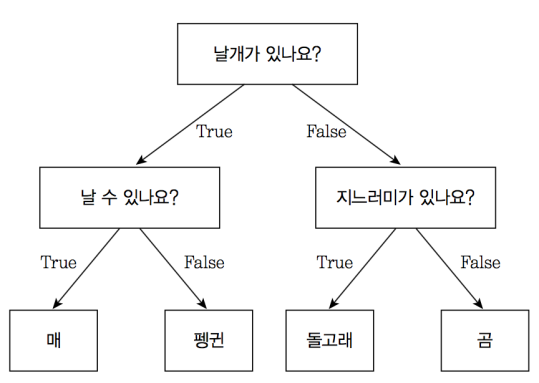
위의 그림은 결정 트리 모델의 예시이다.O / X로 나뉘도록 설계되어 있다.
처음의 분류 기준이나 질문을 Root Node, 마지막 노드들을 Terminal Node 또는 Leaf Node라고 한다. 위의 예시에서는 '날개가 있나요?'가 Root Node, '매', '펭귄, '돌고래', '곰'이 Terminal Node라고 볼 수 있다.

Decision Tree 알고리즘 과정

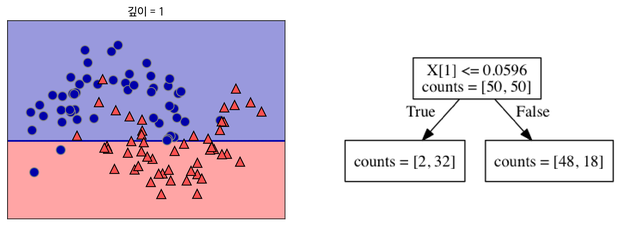
step1
이처럼 데이터를 가장 뚜렷하게 구분할 수 있는 기준으로 분류해준다.

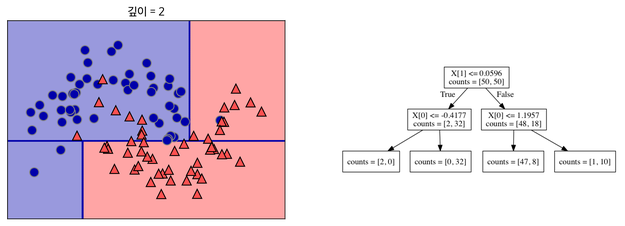
분류된 데이터들을 잘 나눌 수 있는 기준을 만들어준다. 이 과정을 반복한다.

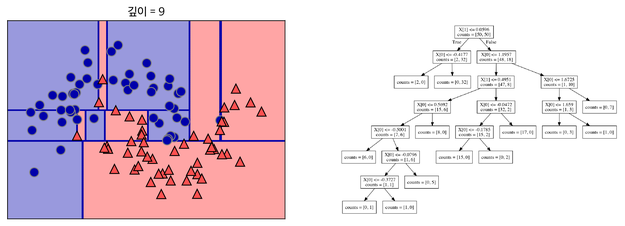
지나치게 많이 기준을 세워 분류할 경우 위의 그림처럼 오버피팅이 발생할 수 있다. 결정 트리에 아무 파라미터를 주지 않고 모델링을 할 경우에도 오버피팅이 발생할 수 있다. -> 무슨 의미일까...
cmd조장님께 자문을 구한 결과 아무 파라미터도 주지 않을 경우 트리가 적정 수준에서 잘라지지 않고 훈련데이터에 너무 맞추려고 해서 오버피팅이 발생한다는 것이다.

Pruning(가지치기)

오버피팅을 줄이기 위한 전략이다. 오버피팅은 트리에 가지가 지나치게 많을 때 나타나기에 최대 깊이나 Terminal Node의 최대 개수 등을 제한하는 작업을 해주는 것이다.

min_sample_split이라는 Parameter를 조정하여 한 노드에 들어있는 최소 데이터 수를 정할 수도 있다.
ex) min_sample_split = 5이면 한 노드에 5개의 데이터가 존재할 때 해당 노드는 더이상 나누어지지 않는다.
max_depth(최대 깊이)를 조정할 수도 있다.
ex) max_depth = 3이면 깊이가 3보다 크게 가지치기를 하지 않는다.

Entropy와 Impurity

Impurity(불순도)는 주어진 범위 안에 다른 데이터가 섞인 정도를 뜻한다.
Entropy(엔트로피)는 불순도를 수치적으로 나타낸 척도이다.

위의 그림처럼 데이터가 분류됐다고 했을 때 항아리 1과 항아리 3은 불순도가 최소, 즉 순도(Purity)가 최대이고 항아리 2는 항아리 1과 3보다 불순도가 높으며 최대이다. 불순도는 서로 다른 데이터들이 같은 양만큼 들어있을 때가 최대이고 하나의 데이터만 있을 때 최소이기 때문이다.
결정 트리는 불순도를 최소로 하는 방향으로 학습을 진행한다.
엔트로피가 높다는 것은 불순도가 높다는 뜻이며, 엔트로피가 1일 때 불순도가 최대, 즉 서로 다른 데이터들이 같은 양만큼 존재한다는 뜻이다.

엔트로피의 공식은 위와 같다. 쳐다봐도 이해될 리 없으니 넘어간다. 참고로 이 때 Pi는 한 영역 안에 존재하는 데이터 중 범주 i에 속하는 데이터의 비율을 의미한다.
다만 두 개의 데이터 범주가 있고 각각 같은 양의 데이터가 있을 때는 Pi가 둘 다 0.5일테니 공식에 넣어주면 정확히 1이 나온다. 앞서 설명한 엔트로피가 1일 때 불순도가 최대라는 점과 맞아 떨어짐을 알 수 있다.

Information Gain

Information Gain(정보 획득)은 분기 이전의 엔트로피에서 분기 이후의 엔트로피를 뺀 수치이다. 엔트로피가 1에서 0.7로 바뀌었다면 0.3만큼 정보를 획득한 것이다.

Information_Gain = entropy(parent) - [weighted average]entropy(children)

위와 같이 공식화할 수 있다. 이 때 weighted average로 분기 이후의 엔트로피의 가중 평균으로 써준 것은 분기시 범주가 2개 이상으로 나누어지기 때문이다. 만약 범주가 1개일 때라면 가중 평균을 안넣어도 된다.

앞서 결정 트리는 불순도를 최소화하는, 즉 엔트로피를 줄이는 방향으로 학습을 진행한다고 언급한 바가 있다. 같은 맥락으로
결정 트리는 정보 획득을 최대화하는 방향으로 학습이 진행된다.

Gini Index

Gini Index(지니 계수)는 0일 때 가장 균일하고 1에 가까이 갈수록 균일하지 않게 된다. 따라서 지니 계수가 낮은 속성을 기준으로 분할한다.

정보 획득 계수와 지니 계수가 정보 균일도를 측정하는 대표적인 방법이다. 정보 획득이 높거나 지니 계수가 낮은 조건을 택하며 자식 트리 노드에 걸쳐서 반복적으로 분할한다.

실습

class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0,
max_features=None, random_state=None, max_leaf_nodes=None,min_impurity_decrease=0.0,
min_impurity_split=None, class_weight=None, presort='deprecated', ccp_alpha=0.0)

Parameter

max_depth: 트리의 최대 깊이를 규정한다. default는 none으로 이 경우 min_sample_split보다 작아질 때까지 깊이를 늘린다. 이 경우 과적합이 될 수 있기에 적절한 값을 설정해주어야 한다.
min_sample_split: 노드를 분할하기 위한 최소한의 샘플 데이터의 수로, 과적합을 줄이는데 필요하다. default는 2로, 작은 값일수록 과적합이 더 잘 나타난다.

결정 트리의 max_depth와 min_sample_split에 제한이 없으면 한 범주에 한 데이터만 남을 때 까지 분류되므로 이를 정해주어서 오버피팅을 막아야 한다.