학습 전

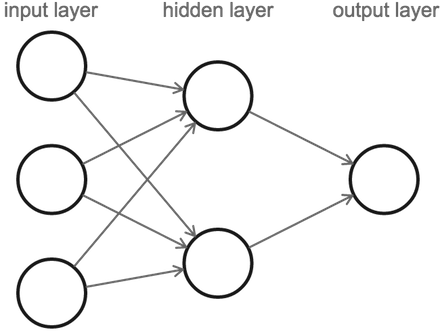
• 신경망은 크게 입력층, 은닉층, 출력층으로 구성된다.
  

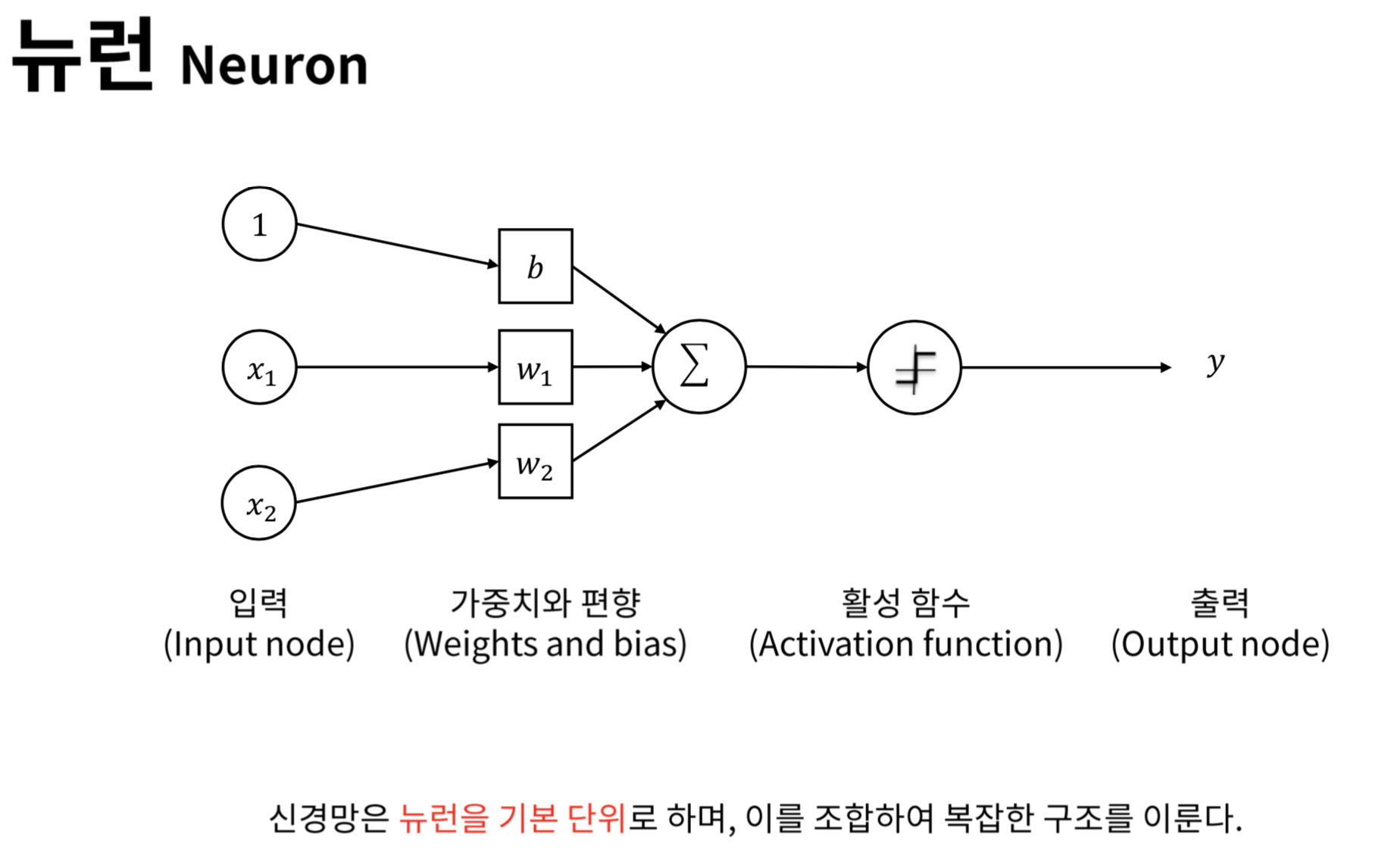
• x1, x2는 입력 신호이며, 입력 신호가 다음 노드로 보내질 때에 가중치가 곱해진다. w1, w2는 가중치, b는 편향이다.

• w1*x1 + b = a

• y = h(a)
  가중치와 입력신호의 곱에 편향이 더해진 값이 활성화 함수에 들어간다. 활성화 함수에서 계산을 통해 나온 값 y는 다음 노드의 신호가 되고 또다시 가중치가 생기고 이 과정이 출력층까지 반복된다.

• 활성화함수를 사용하는 것은 비선형성 함수를 통해 선형의 데이터가 아니더라도 분류나 회귀가 가능하도록 하며, 층을 깊게 쌓을수록 학습이 잘되어 정확도를 높일 수 있기 때문이다.

• 활성화함수를 선형으로 사용할 경우 은닉층을 몇 개를 쌓더라도 일차식을 거듭하면 일차식에 불과하므로 층을 쌓는 의미가 없게 된다.

• 출력층이 여러 노드로 구성된 경우에는 주로 활성화 함수로 소프트맥스를 이용한다. 이를 통해 각 노드에 대한 확률을 구할 수 있다.

학습

학습의 목표는 정확도를 개선하는 것이다. 이를 위해서는 정확도가 높을 때의 최적의 매개변수를 찾아야 한다.

• 훈련 데이터 - 학습에 사용됨 -> 최적의 매개변수 찾기!!
• 시험 데이터 - 평가에 사용됨
  오버피팅: 훈련 데이터에 너무 맞추어져서 시험 데이터에서 좋은 성능을 보이지 못하는 경우
• 손실함수: 최적의 매개변수(가중치)를 구하기 위한 함수이다
  손실함수에는 오차제곱합, 교차 엔트로피 오차 등이 있다. 쉽게 말하면, 정답 레이블과 예측 값을 비교하는 것이다.
  오차제곱합이나 교차 엔트로피 오차 모두 정답 레이블과 예측 값을 비교하는데, 정답과 다를수록 손실함수의 값이 커진다.
  즉, 손실함수의 값이 작아질수록 정답에 근접해지고, 최적의 가중치를 구할 수 있게 된다.

=> 손실함수를 최소화하는 방향이 최적의 매개변수(가중치)를 구하는 방향이고, 정확도를 높이는 방향이다.

손실함수의 최적값을 구하는 방법: 경사하강법
w := w - a*기울기
가중치에 학습률 X 손실함수의 기울기를 뺀 값을 가중치로 업데이트한다.
학습률은 0.1이나 0.01정도가 적당하며, 하이퍼파라미터로 인간이 직접 설정하는 매개변수이다.

이 때 기울기가 양수이면 가중치에 양수를 빼니 그래프상에서 x축에서 왼쪽으로 이동하여 더 함숫값이 작은 방향으로 이동하고, 기울기가 음수이면 가중치에 음수를 빼니 그래프 상에서 x축에서 오른쪽으로 이동하여 더 함숫값이 큰 작은 방향으로 이동한다. 즉 점차적으로 극솟값에 가깝도록 이동한다.

그래프에서 x축으로는 가중치가 들어가고 함수는 비용함수(cost function)이다.

• loss function: 손실함수로 구한 개별적인 값
• cost function: 손실함수로 구한 값들의 합(시그마가 들어간 거라고 생각하면 된다)

이 때 경사하강법으로는 궁극적으로 '극솟값' (local optimum)을 구한 것이므로 이는 최솟값은 아닐수도 있다. 이는 모멘텀 등으로 극복할 수 있다.

이렇게 손실함수의 값이 최솟값이 되는 때를 구했을 때의 가중치가 최적의 매개변수가 되며, 이를 찾는 과정이 신경망 학습이다