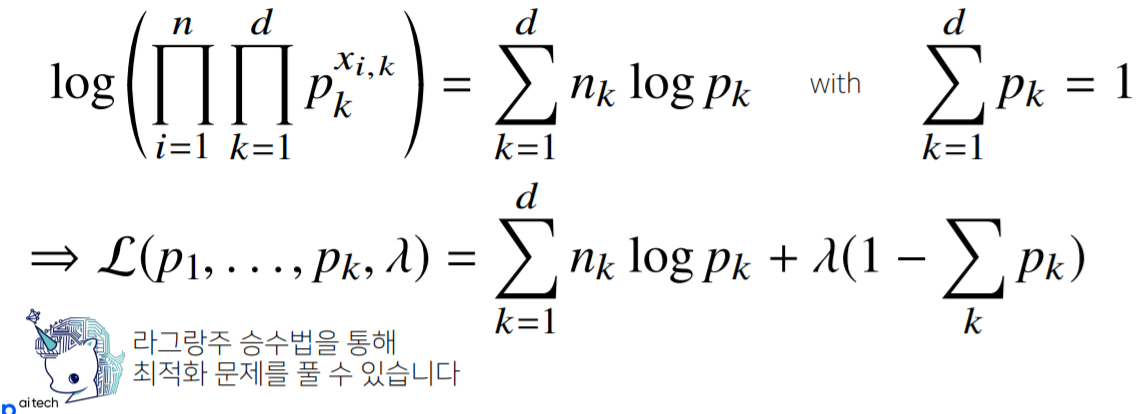본 포스팅은 네이버 부스트캠프 3기를 통해 공부한 내용을 기반으로 작성된 글입니다.
모수란?
- 통계학에서 모수는 모 평균, 모 표준 편차, 모 분산 등 모집단의 데이터를 의미함
베르누이 분포 : θ = μ
이항분포 : θ = ( N, μ )
정규분포 : θ = ( μ, σ2 )
통계적 모델링은 적절한 가정 위에서 확률분포를 추청하는 것이 목표
머신러닝과 통계학이 공통적으로 추구하는 목표
유한한 개수의 데이터만 관찰하여 모집단의 분포를 정확히 알아낼 수 없으므로 근사적으로 확률분포 추정
모수적 방법론 : 데이터가 특정 확률분포를 따른다고 가정한 후, 그 분포를 결정하는 모수를 추정하는 방법
1) 확률분포 가정
-
데이터가 2개의 값(0 or 1)만 가지는 경우 -> 베르누이 분포
-
데이터가 n개의 이산적인 값을 가지는 경우 -> 카테고리 분포
-
데이터가 [0,1] 사이에서 값을 가지는 경우 -> 베타 분포
-
데이터가 0 이상의 값을 가지는 경우 -> 감마분포, 로그정규분포 등
-
데이터가 R 전체에서 값을 가지는 경우 -> 정규분포, 라플라스 분포 등
기계적으로 확률분포를 가정해서는 안되고, 데이터를 생성하는 원리는 먼저 고려해야 함
2) 모수 추정
정규분포의 모수(평균 μ, 분산 σ2)로 추정하는 통계량 알아보기

표본평균의 표집분포(=통계량의 확률분포)는 N이 커질수록 정규분포를 따릅니다.
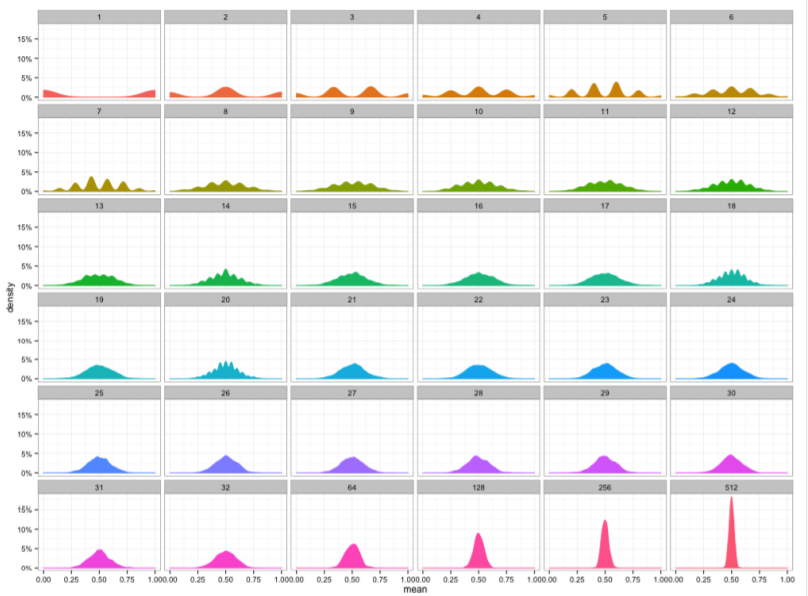
데이터의 크기 N이 커질수록, 평균값은 하나로 몰리고 분산이 작아짐
Maximum likelihood estimation (MLE)
-
표본평균이나 표본분산은 중요한 통계량이지만, 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라짐
-
이론적으로 가장 가능성 높은 모수 추정법 중 하나가 최대가능도 추정법(MLE)

- 데이터 집합 X가 독립적으로 추출되었을 경우 로그가능도를 최적화함
Why?
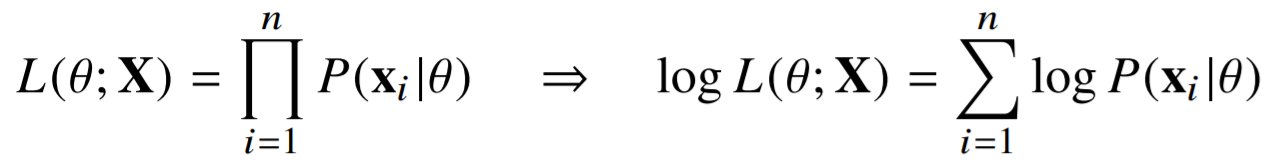
데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로 가능도를 계산하는 것은 불가능 (연산 오차 발생)
-
데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 덧셈으로 바꿀 수 있어 컴퓨터로 연산이 가능
-
경사하강법으로 가능도를 최적화할 때, 미분 연산 시 로그가능도를 사용하면 연산량을 줄일 수 있음
연산 복잡도 감소 : O(n2) -> O(n)
최대가능도 추정법 예제
- 정규분포 (연속)
정규분포를 따르는 확률변수 X로부터 독립적인 표본 {X1,...,Xn}을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
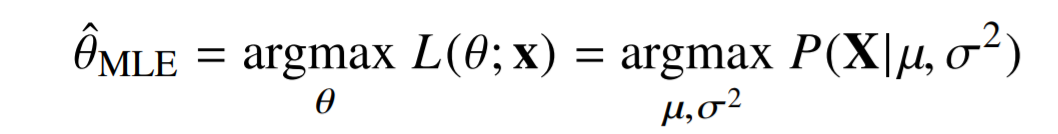
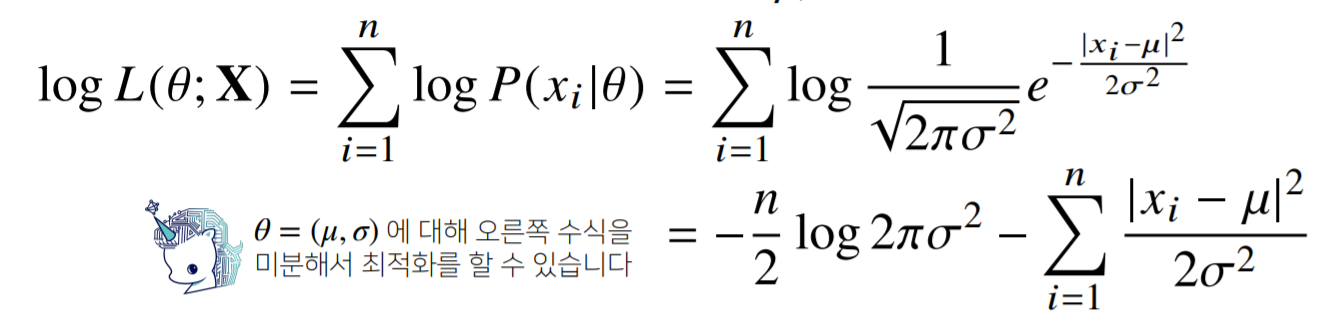
- 미분이 0이 되는 평균과 분산을 찾으면 가능도 최대화
1) 평균
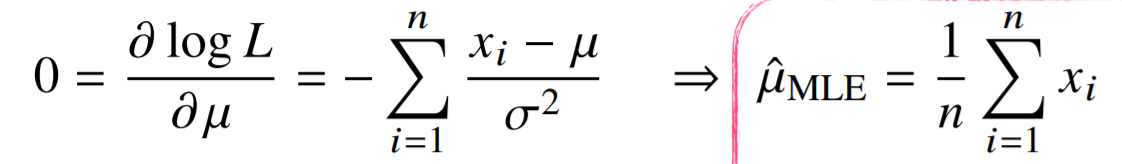
2) 분산
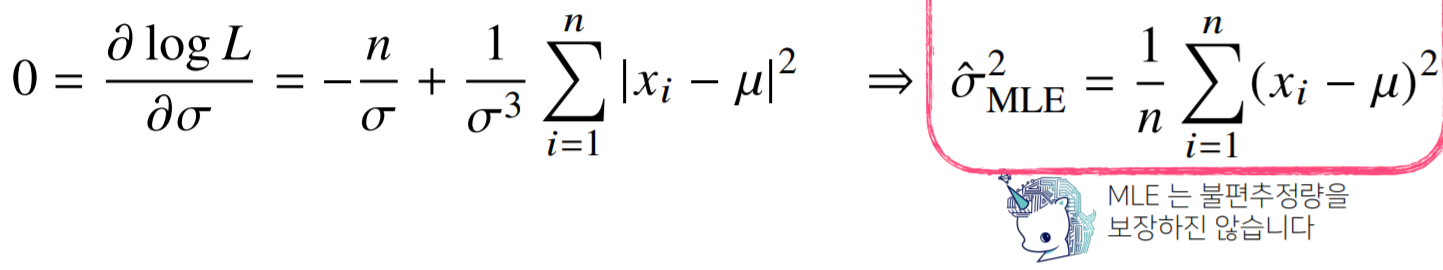
- 카테고리 분포 (이산)
카테고리 분포 Multinoulli(x;p1,...,pd)를 따르는 확률변수 X로부터 독립적인 표본 {x1,...,xn}을 얻었을 때, 최대가능도 추정법을 이용하여 모수를 추정하면?

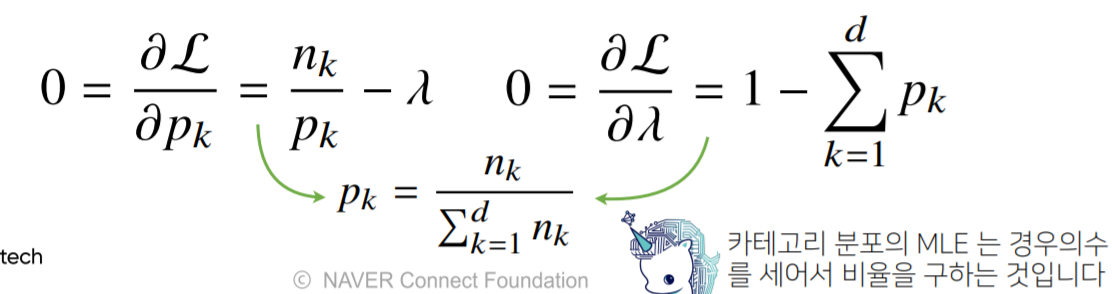
식을 다시 정리하면,
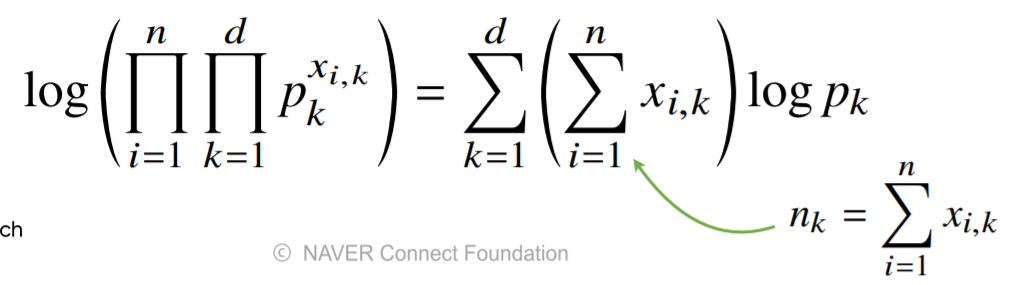
제약식과 함께 식을 세워서 모수 추정 가능