📚 t 분포란?
💡 분포는 정규분포와 생김새가 비슷하지만, 꼬리가 더 두껍고 길다는 차이점이 있다.
💡 표본평균을 이용해서 정규분포의 평균을 해석할 때 많이 사용한다.
💡 가설검정이나 회귀분석에도 많이 쓰인다고 한다.
💡 좌우 대칭이다.
🧐 모분산 없이 표본평균의 분포를 알아보자 ?!
모집단이 정규분포를 따를 때, 표본평균은 을 따르게 된다.
다만 이 때 표본의 수가 정말 많다면 어차피 모분산 의 영향력이 없다시피 하겠지만, 표본 수가 작을 때는 모분산을 정확히 알기 어려우므로 문제가 생긴다. 정규분포의 모양을 특정하기도 어렵고, 전반적인 정규분포를 이용한 검정이 그 신뢰도를 잃게 된다.
이를 보완하기 위해 정규분포와 형태가 비슷하지만 모분산 항을 포함하지 않고, 대신 표본분산을 쓰는 분포를 고안했고 그것이 바로 💡t 분포 되시겠다.

모분산이 쓰이지 않고 표본분산만 쓰인다.
👨🏫 t분포의 자유도
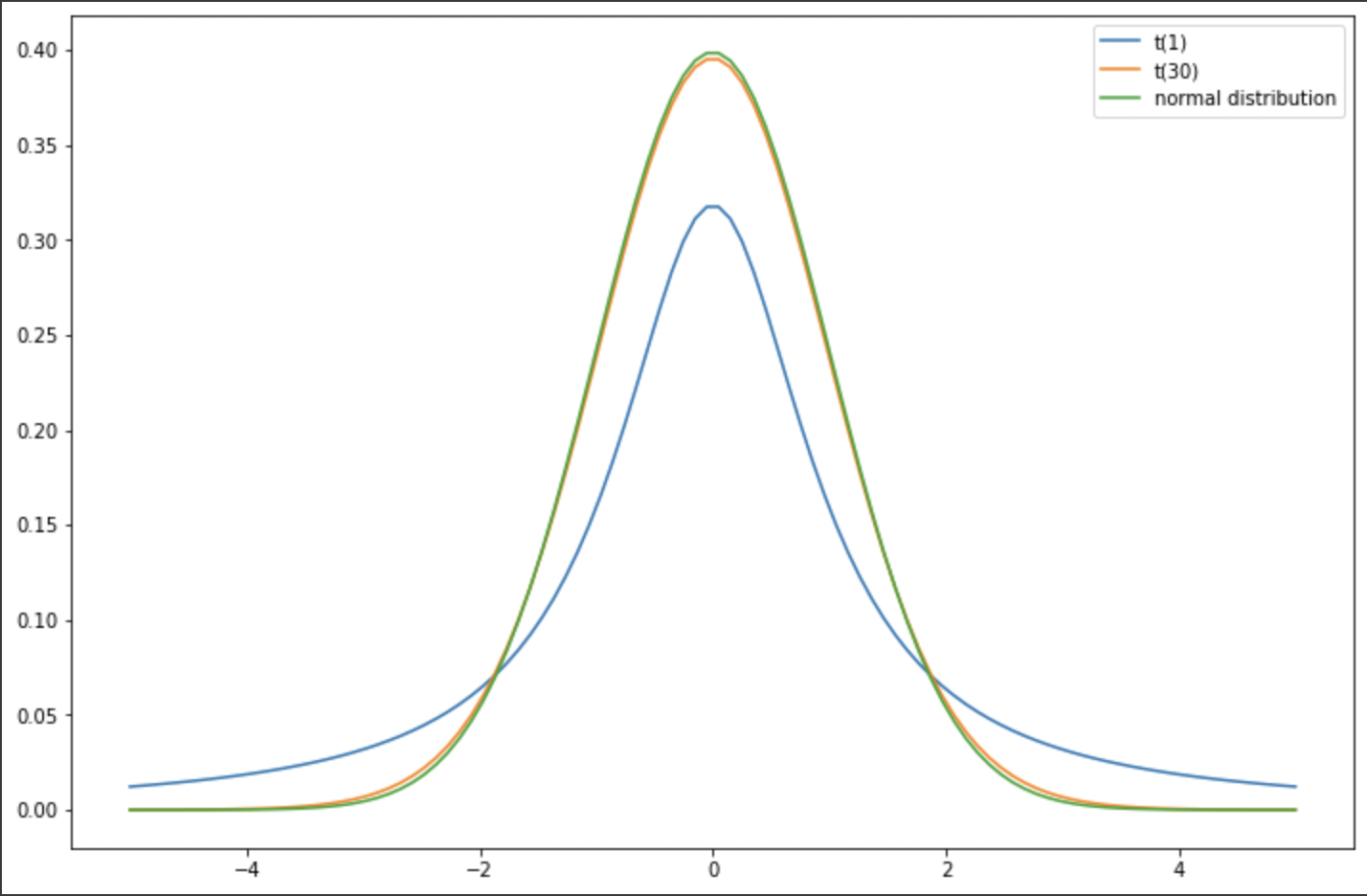
출처 : KHUDA 구태형 선생님 ㅎ ㅎ
분포의 는 자유도를 뜻한다. 자유도는 표본의 수와 연관성이 있다.
위 사진처럼 자유도가 커질수록 그래프는 표준정규분포와 비슷해지고, 자유도가 적어지면 그래프는 점점 옆으로 퍼진다.
이는 분포가 표본의 수가 많아질수록 정규분포와 비슷해진다고 해석할 수 있다. 보통은 이면 정규분포에 근사한다고 한다
t-검정
💡 모양
분포는 정규분포에 비해 꼬리가 두껍고 길다. 이는 검정에 관점에서 바라봐야 한다.
📚 정규분포의 경우, 중심에서 조금만 벗어나도 결과가 크게 달라질 수 있다.
💡 But 분포의 경우, 꼬리가 두껍고 길다=데이터가 중심에 쏠려있지 않다 이므로 중심에서 벗어나도 상대적으로 안전하다.
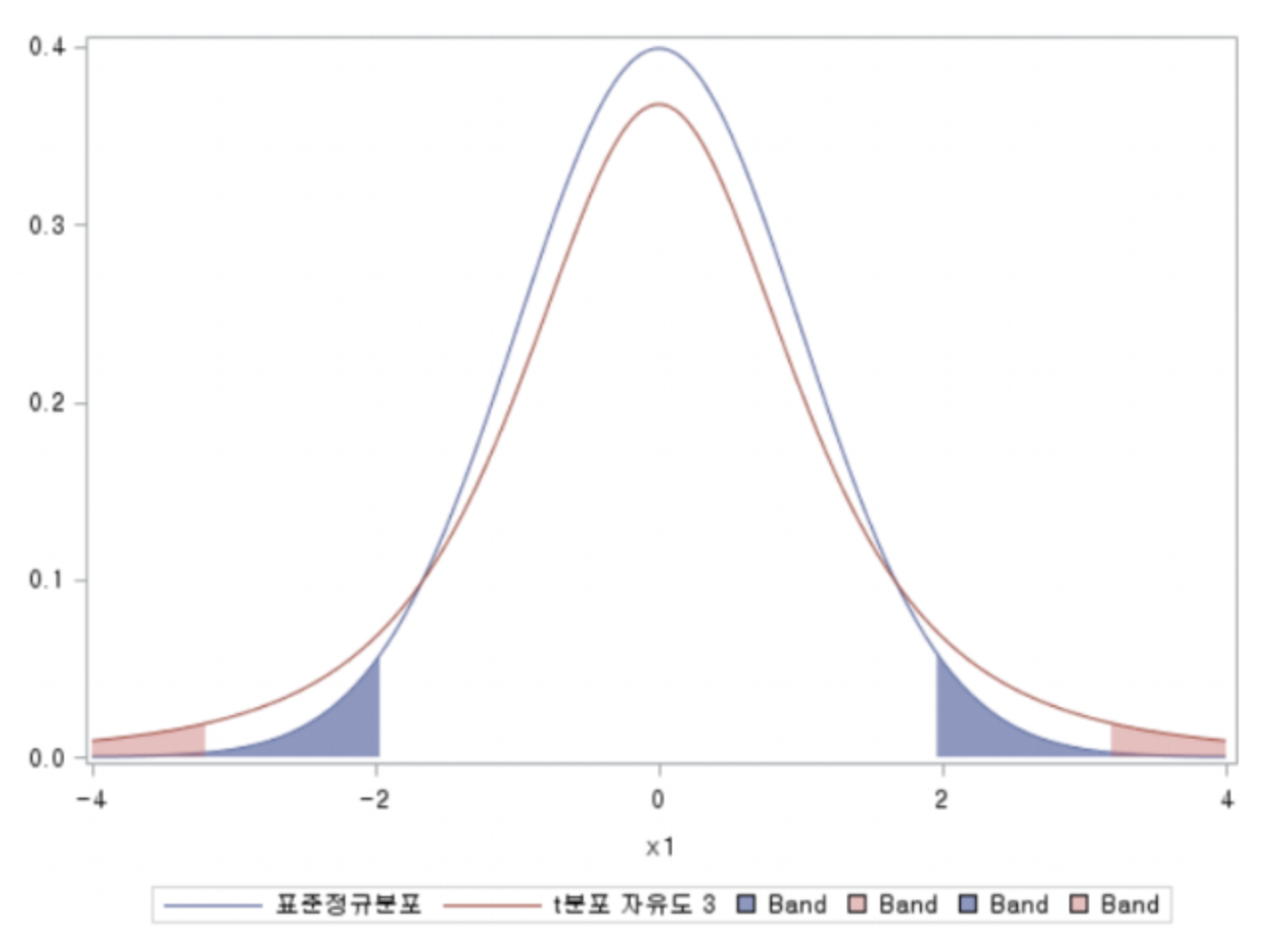
위 그림은 좌우 각각 2.5%의 데이터를 색칠한 그림이다. 분포의 경우 데이터가 훨씬 사이드로 퍼져있지만, 표준정규분포의 경우 그렇지 않다는 것을 알 수 있다.
🧐 표준정규분포로 해석했을 때는 중심에서 2만 벗어나도 결과가 달라질 것이지만,
💡 분포로 해석한다면 중심에서 3 벗어나도 결과가 동일할 것이다.
이러한 결과를 '보수적 검정' 이라고 표현하는데, 아무래도 안전빵같은 느낌이라서.
💡 검정통계량 t-값
검정에 쓰이는 검정통계량. 두 집단의 평균 차이를 표준오차(SE)로 나눈 값.

위에서 봤던 사진과 같다.
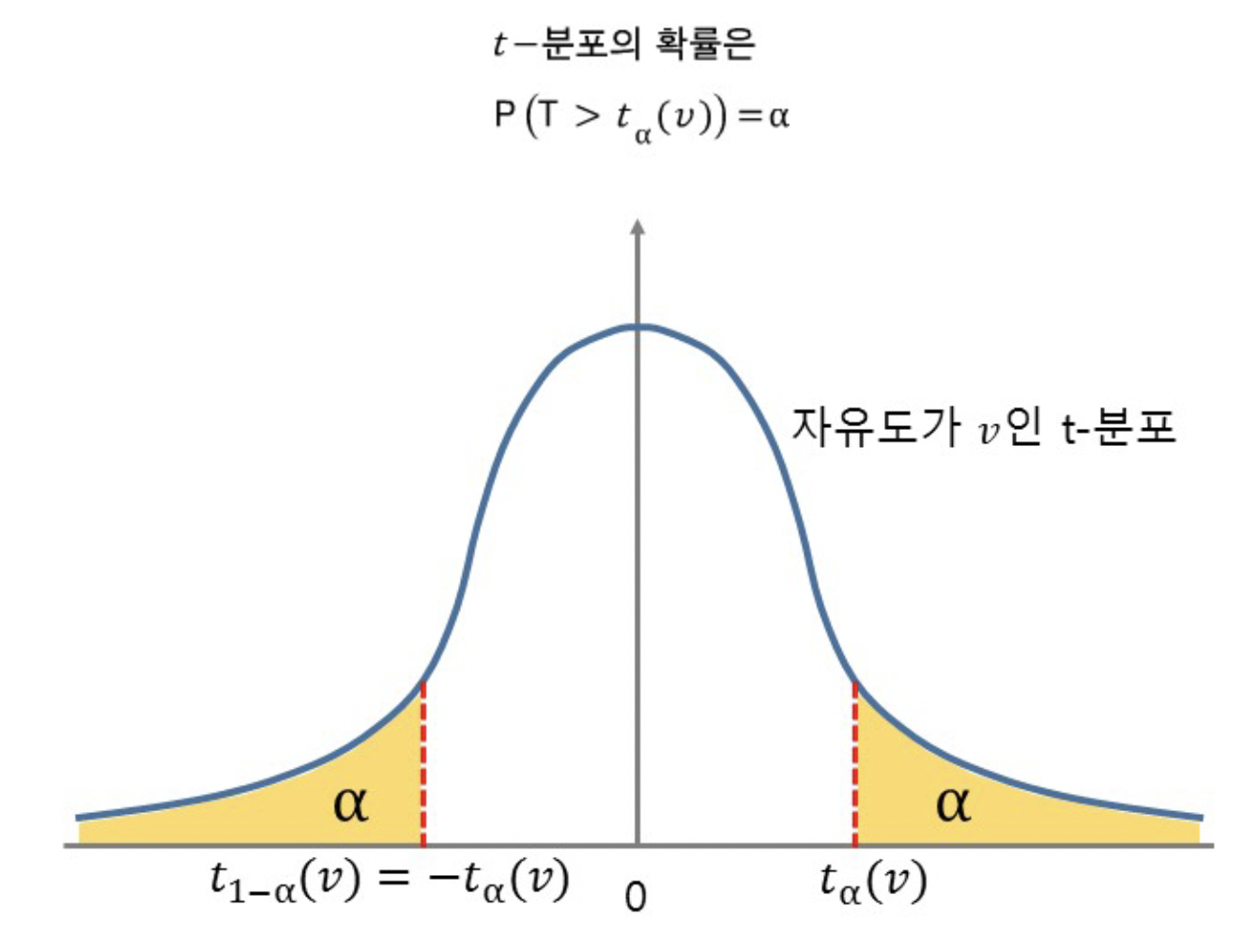
출처 : https://m.blog.naver.com/mykepzzang/220853827288
t-분포의 확률은 위 사진과 같다. 근데 저 꼬라지 함수는 어딘가 좀 낯이 익은데, 카이제곱분포의 그것과 비슷하게 생겼다.
역시 분포도 그 통계량을 구하기가 어려워서 표가 따로 있다.
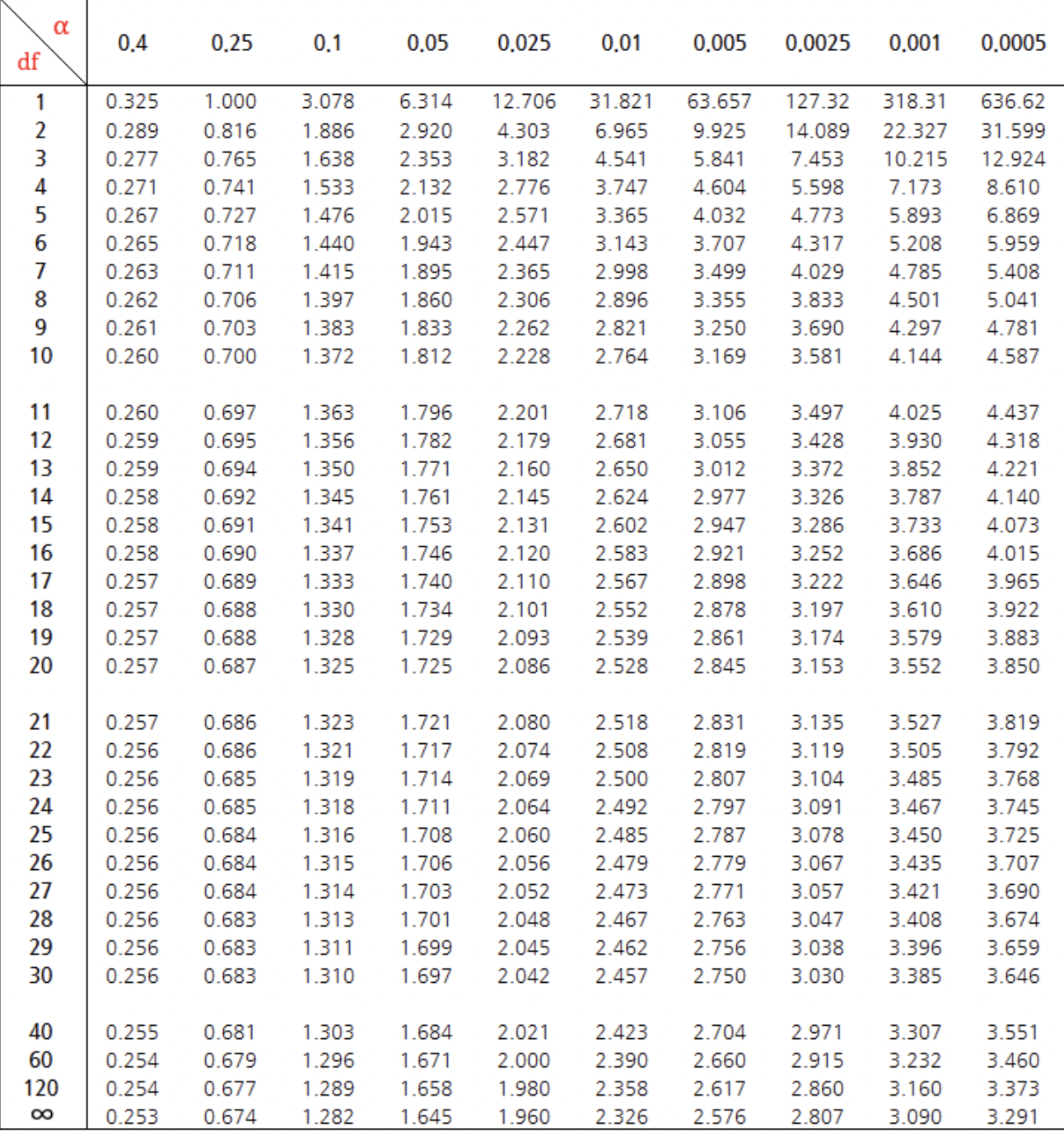
출처 : https://math100.tistory.com/43

출처 : https://m.blog.naver.com/sendmethere/221333164258
분포들과 그에 따른 검정방법들을 보다보니, 약간 다들 공통점이 있는 것 같다.
분포 자체에 대해서도 공부를 해야겠지만, 유의확률과 유의수준에 대한 이해가 중요한 것 같다.
