📚 푸아송 분포 (Poisson Distribution)

푸아송 분포의 확률밀도함수는 다음과 같이 정의된다.

이는 주로 일정한 시간 혹은 공간 단위에서 평균적인 사건의 수에 대한 분포를 나타낸다. (일정 시간 발생하는 트래픽, 1시간동안 걸려오는 전화...)
푸아송 분포는 파라미터 $\lambda$를 사용한다. (평균=분산=$\lambda$)

이 때 람다는 일정 구간 안에서 발생한 평균 사건의 수가 된다.

📚 평균과 분산

증명은 생략하겠지만, 푸아송 분포의 평균과 분산은 파라미터 그대로 람다가 된다.
확률변수 $X$가 푸아송 분포를 따를 때, $X$의 평균과 분산은

📚 그리기

import numpy as np
import matplotlib.pyplot as plt
from math import factorial, exp

# Probability density of the Poisson distribution
def pois_dist(n, lamb):
    pd = (lamb ** n) * exp(-lamb) / factorial(n)
    return pd


x = np.arange(40)
pd1 = np.array([pois_dist(n, 10) for n in range(40)])
plt.ylim(0, 0.15)
plt.text(33.5, 0.14, 'lamb = 10')
plt.bar(x, pd1, color='lightcoral')
plt.show()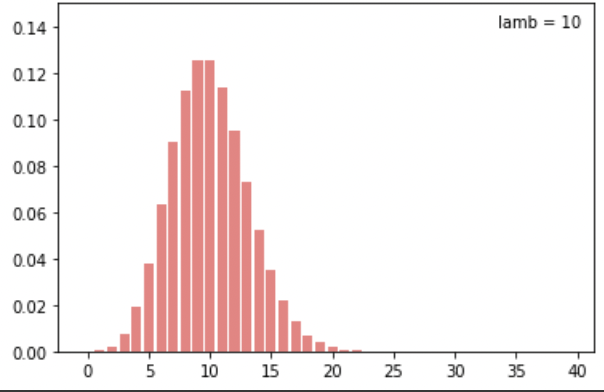

신기하게 생긴 친구다.

참고
https://codetorial.net/articles/poisson_distribution.html