이번에 다룰 친구는 아주아주 유명한 분포인 정규분포!

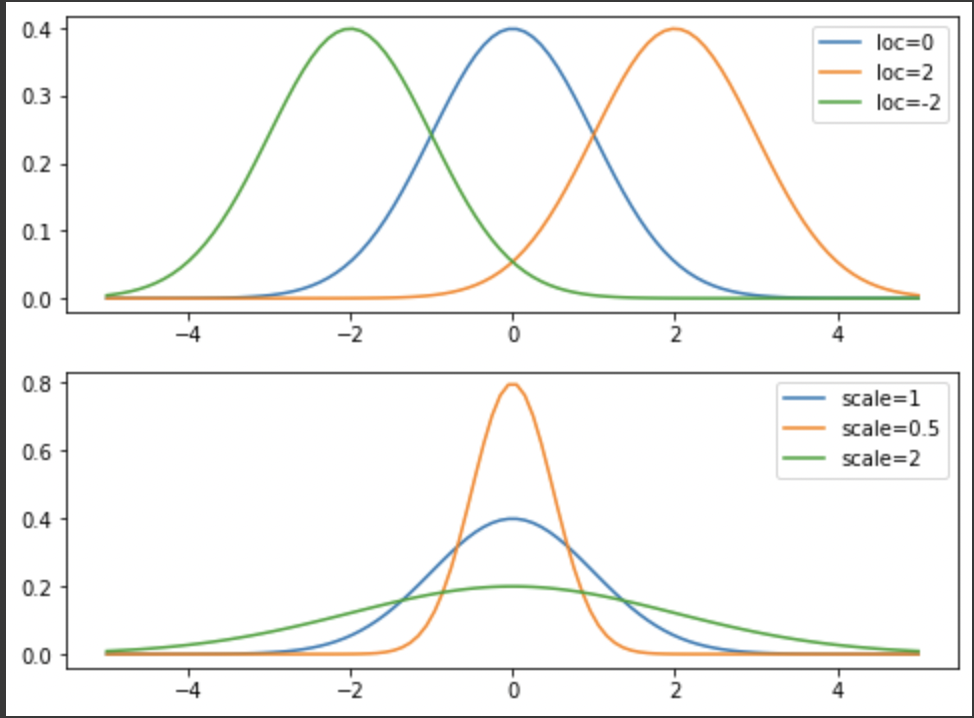
이미지 출처 : KHUDA 구태형 선생님 <3

📚 About 정규분포

정규분포는 통계학에서 대표적인 연속 확률분포로, 다음과 같은 그지같은 확률밀도함수를 가지고 있다.

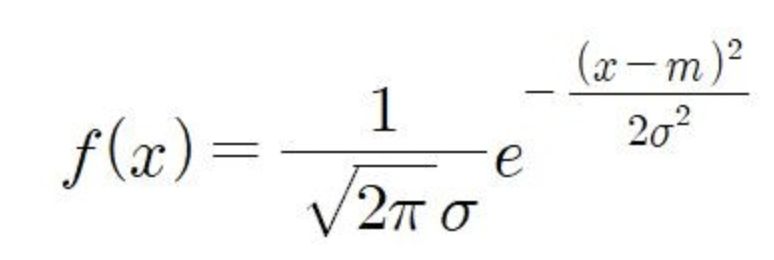
정규분포 곡선은 종 모양으로 아래와 같다.

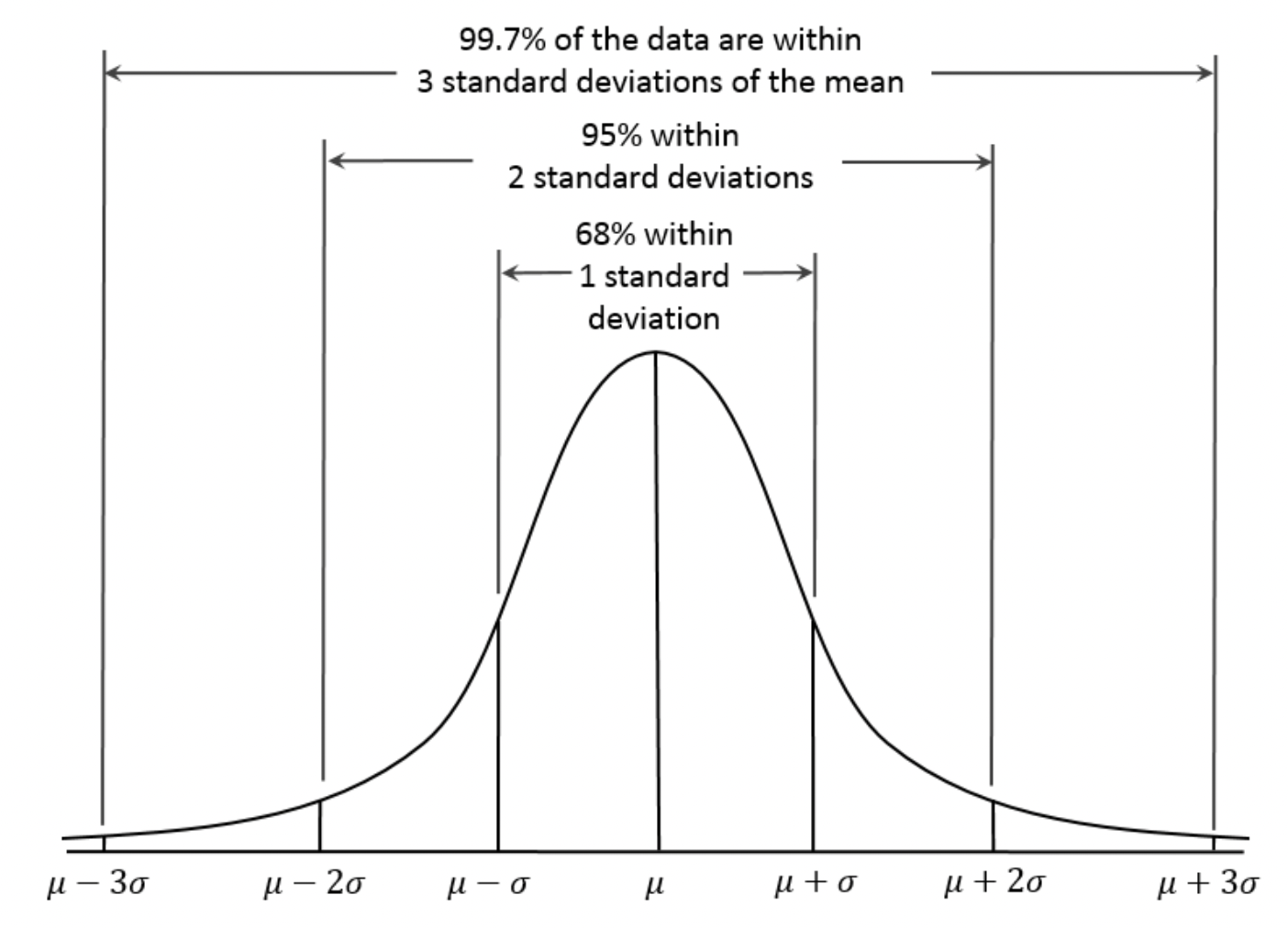
출처 : 과학기술정보통신부 블로그

사실 이 중에서도 가장 많이 사용되는 것은 표준정규분포이다.

📚 표준정규분포

표준정규분포는 평균이 0, 표준편차가 1인 정규분포를 말한다.
모든 정규분포는 표준화 과정을 통해서 이렇게 표준정규분포로 나타낼 수 있다.

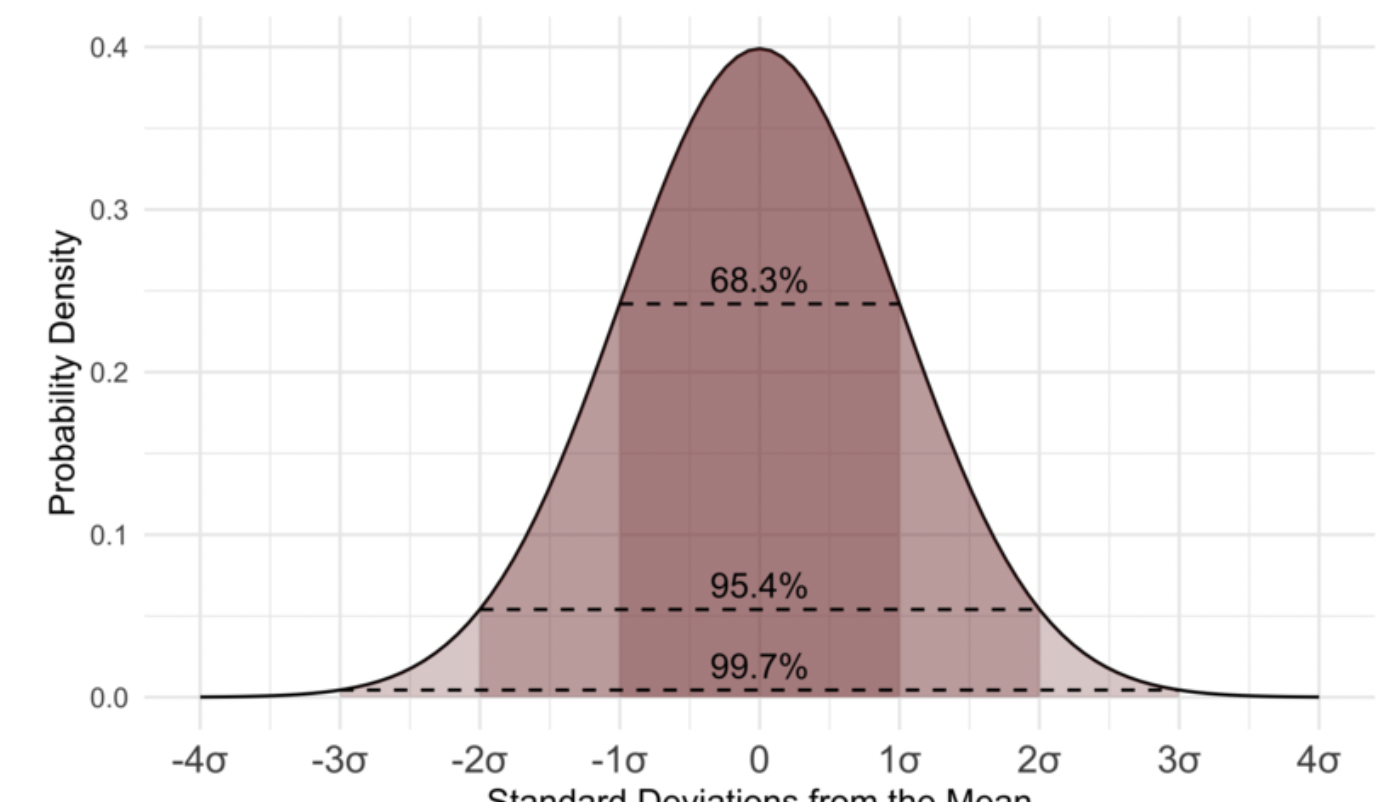
표준화 과정은 $N(m, \sigma^2) \rarr N(0, 1^2)$ 로 바꿔주는 과정이다.

우선 정규분포의 확률변수를 $X$라고 하자. 평균을 0으로, 표준편차를 1로 만들어주면 된다.
$E[X] = m$일 때, 평균이 0이 되려면 $E[X-m]=E[X]-m=0$을 이용하면 된다. (평균의 성질)
따라서 확률변수를 $X\rarr X-m$으로 바꿔주면 된다.

표준편차를 1로 만들기 위해서 분산도 1로 만들어줘야 한다.
$V[X] = \sigma^2 \rarr V[X-m] = \sigma^2 \rarr V[\frac{X-m}{\sigma}]=(분산의 \, 성질에\, 의해)\frac{V[X]}{\sigma^2}=1$

따라서 확률변수는 $X \rarr X-m \rarr \frac{X-m}{\sigma}$로 바꿔주면 된다.
얘를 $Z$라고 놓으면 이 변수는 표준정규분포를 따르게 된다.

$\frac{X-m}{\sigma}=Z\sim N(0, 1)$

이렇게 표준화 과정을 거치면 표준정규분포표를 이용해서 원하는 확률 값을 구할 수 있게 된다.

📚 표준정규분포표

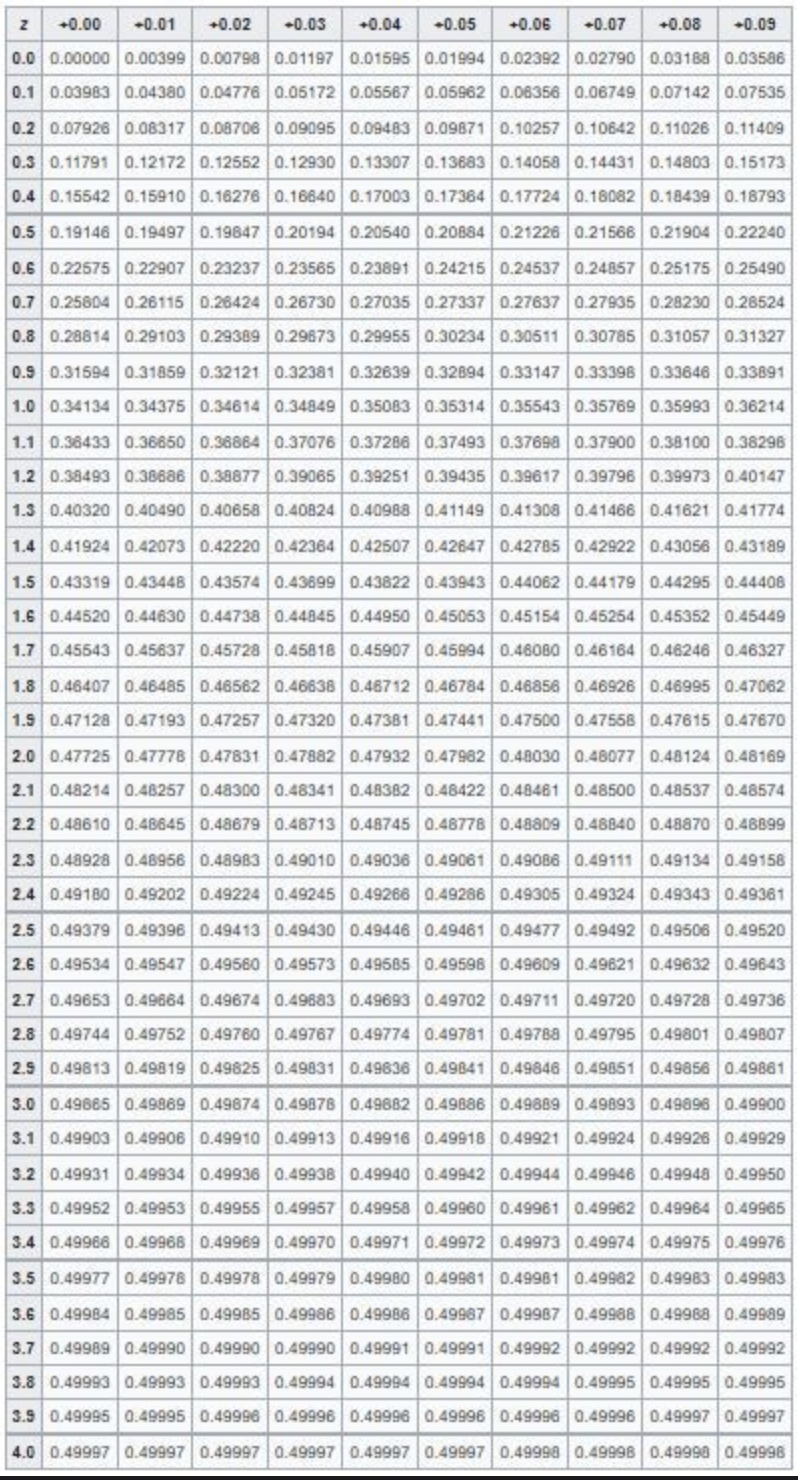
출처 : 과학기술정보통신부 블로그

위 표를 이용하면 $Z$값에 맞는 연속확률분포의 값을 담고 있는 표이다.
연속확률분포는 그래프 아래 면적을 통해 확률을 구하게 되는데, 이 면적을 정리해 놓은 것.
즉 표준화된 확률변수의 값을 알면, 해당 값의 확률을 쉽게 구할 수 있다.

이 때 표에 음수는 없다는 것을 알아챌 수 있는데, 표준정규분포는 🚨좌우대칭🚨 으로 형성되기 때문에 양수나 음수나 값이 같다.

이를 통해서 특정 구간에 속할 확률도 구할 수 있다.

📚 예제 : 이항 분포를 정규분포로 근사하여 확률을 구해보자.

출처 : KHUDA 구태형 선생님 <3

Q. 연속성 수정을 고려한 이항분포의 정규분포 근사

대학생 중 20%는 밖에 나가기 싫고 항상 집에 있고 싶다고 한다. 대학생 중 100명을 표본추출하여 이에 대해 물어봤을 때, 16 ~ 19명 사이로 집에 있고 싶어하는 학생이 있을 확률을 구해보자.

😵‍💫 1) 이항분포를 통해 대략적인 식만 나열해보기
$nCr\,p^x(1-p)^{(n-x)}$

$∑_{i=16}^{19}100Ci(0.2)^{i}(0.8)^{100-i}$

😵‍💫 2) 연속성 수정을 고려해 정규분포에서의 범위 구해보기
집에 있고 싶어하는 학생의 확률 = 0.2 (p)
평균=np=100(0.2)=20
표준편차$\sqrt{npq}$=(100)(0.2)(0.8) ( 이항분포의 평균과 표준편차는 $np$와 $npq$이다)

2-1) x=16일 때 표준점수
연속성 수정 = x-$\frac12$ = $\frac{31}2$
$z=\frac{X - \bar{x}}{\sigma}$=-$\frac98$

2- 2) x=19일때 표준점수
$z=-\frac18$
따라서 정규분포에서의 범위 $[-\frac98, -\frac18]=[-1.125, -0.125]$

-1.13 정규분포표값(반올림) = 0.3708

🤩 3) 16 ~ 19명 사이로 집에 있고 싶어하는 학생의 수 구해보기(인터넷 정규분포표참고)

-1.13 정규분포표값(반올림) = 0.3708
-0.13 정규분포표값(반올림) = 0.0517
구간 안에 있을 확률 0.3708-0.0517=0.3191

---

🚨 원시 데이터는 거의 정규분포를 따르지 않는다. 그러나 표본들의 평균이나 합계, 오차는 대부분 정규분포를 따른다.