[통계] t검정

hyun·2022년 8월 17일

KHUDA 스터디 통계

통계

목록 보기

23/37

👕 t분포와 t검정

이전 포스팅에 정리해둔 게 있다.
[통계] t분포
간단하게 다시 복기해보자.

📚 t분포

모분산을 이용하지 않고 표본평균의 분포를 가늠할 수 있도록 하는 분포다.
표본평균의 분포는 다음과 같은 식을 따른다.

N(\mu, \frac{\sigma^2}{n})

표본의 수가 적을수록 모분산이 끼치는 영향이 커지는데, 모분산을 정확히 알고 있지 않으면 정규분포를 통한 검정이 신뢰도를 잃게 된다.

따라서 모분산을 사용하지 않고,

이렇게 정의되는 T 분포를 만들어냈다.
다만 위에도 써있듯이, 모집단이 정규분포를 따라야 한다는 전제가 깔린다.

자유도에 대한 부분은 [통계] 표본평균과 모평균 (+표준오차, 자유도 ) 참고.

의 확률변수를 사용하는 t분포를 만들어냈다고. (단, $S^2$ =표본분산)

⭐️ t분포의 자유도 (degree of freedom)

t분포의 자유도가 커질수록 정규분포와 비슷해진다.
일반적으로 30보다 큰 자유도에서 정규분포에 근사한다.
자유도가 적어진다=표본의 수가 적다=더 넓은 공간을 커버한다=그래프가 옆으로 퍼진다.

🦎 t 검정

😾 T분포의 모양

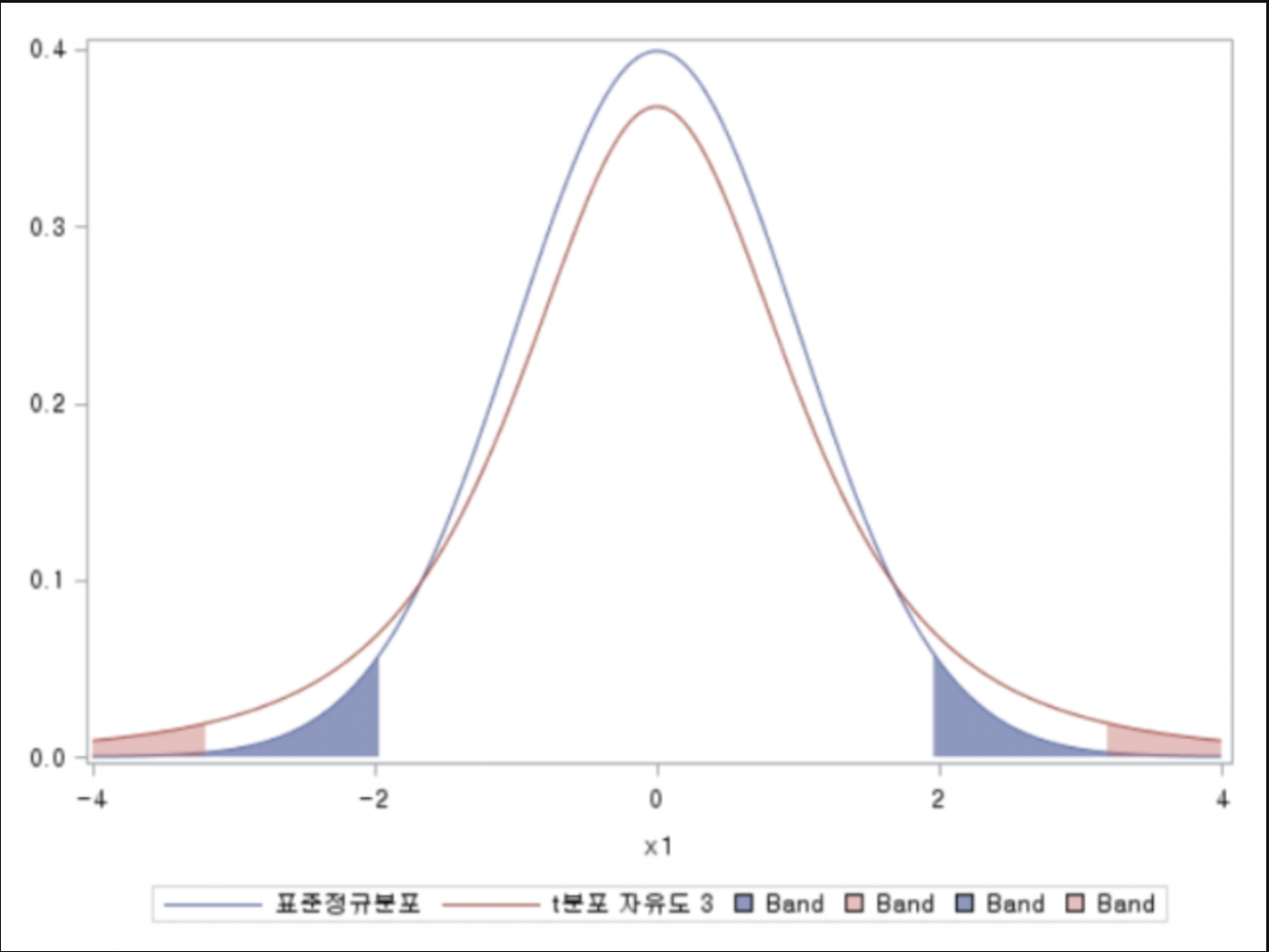
그림은 각 분포의 좌우 2.5%씩을 칠한 것.

t분포는 표준정규분포에 비해 꼬리가 두껍고 길다
= 더 넓은 공간을 커버한다 = 검정에 대한 안정성이 높다.
검정을 한다고 하면, 표준정규분포의 경우 중심에서 2만 멀어져도 값이 달라지겠지만, t분포는 3 멀어져도 동일한 결과를 줄 것이다.
유효한 구간이 더 넓어지는 것 ?

🖤 검정통계량 t값

처음 봤던 사진인데, 검정통계량 또한 이 값을 따른다.
검정통계량과 그에 따른 표를 보는 법도 이전 포스팅에 있다.

[통계] t분포

👕 t검정의 종류

🧐 독립표본(일표본) t-검정 (one sample t-test)

단일 모집단에서 연속형 변수를 특정 값과 비교할 때 사용한다

🎲 대응표본 t-검정 (paired sample t-test)

단일 모집단에 두 번의 처리를 가했을 때, 각 처리에 따른 평균의 비교를 할 때 사용한다
등분산성을 확인하고, 등분산이 전제되지 않으면 이분산 대응표본 t검정을 시행한다.
-> 등분산이 전제되지 않으면 두 집단의 분포가 다르므로 다른 검정이 필요.

여담으로 등분산 검정 시 levene의 F검정을 이용한다.

📚 예제

예제는 다음 블로그를 참고하였다.
https://jae-eun-ai.tistory.com/48#%EC%98%88%EC%8B%9C

😎 독립표본 t-검정

🧐 문제 및 데이터

A과수원에서 생산된 사과의 평균무게는 200g으로 알려져있다. 실제로도 그러한지 알아보기 위해 과수원에서 생산되는 사과 15개를 임의로 뽑아서 무게를 측정해보고, A과수원에서 생산되는 전체사과 무게의 평균이 200g과 같다고 할 수 있는지 검정해보자.

💡 귀무가설 : A과수원에서 생산되는 사과무게의 평균값은 200g이다.
💡 대립가설 : A과수원에서 생산되는 사과무게의 평균값은 200g이 아니다.

다만 t-test는 모집단이 정규성을 따른다는 전제가 필요하다.

😊 정규성 검사

#알려진 평균
mu = 200
#수집된 표본
data = [200,210,180,190,185,170,180,
       180,210,180,183,191,204,201,186]

#데이터가 적어도 30개 이상이면 중심극한 정리를 적용할 수 있지만
#여기서는 데이터 수가 15개 이기 때문에 별도의 정규성 검정이 필요
### 정규성 검정
from scipy.stats import shapiro
shapiro(data)

shapiro-wilk test는 자주 쓰이는 정규성 검정이라 한다. 포스팅감 포착 !

첫 번째 결과는 검정통계량, 둘째 값은 p값이다.
p값이 유의수준인 0.05보다 크다면 우연히 발생하는 범주 안이므로 정규분포를 따른다고 해석할 수 있다.

📦 Box plot

import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('whitegrid')

sns.boxplot(data=data)
plt.title('box plot')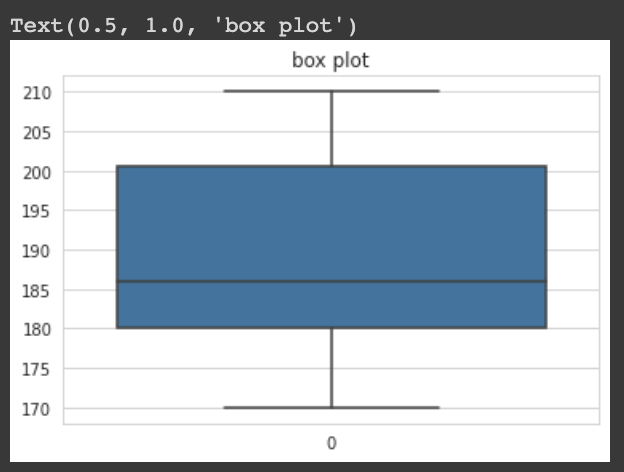

이렇게 그림으로 보면 모평균인 200과 유의미한 통계적 차이가 있는지 구별하기 어렵다.

📚 독립표본 t-검정

# 일표본 t-검정
from scipy.stats import ttest_1samp

ttest_1samp(data, mu)

정통법으로는 t값을 알고 표를 보고 p값을 봐야 하나, 간단하게 나온다.
이 때 pvalue가 유의수준 0.05 미만이므로 평균 200과의 차이는 우연에 의해 발생한 것이 아니라는 결론을 내린다.
결론적으로 주어진 사과들의 평균 무게는 200과는 통계적으로 유의미한 차이가 있다.

✌️ 대응표본 t-검정

10명의 환자를 대상으로 수면영양제를 복용하기 전과 후의 수면시간을 측정하여 영양제의 효과가 있는지를 판단하고자 한다. 표본이 정규성을 만족한다는 가정하에 단측검정을 수행한다.

💡 귀무가설 : 수면영양제를 복용하기 전과 후의 평균 수면시간에는 차이가 없다.(D=0)
💡 대립가설 : 수면영양제를 복용하기 전과 후의 평균 수면시간 차이는 0보다 작다.(D<0)

🎮 데이터 생성

import pandas as pd
before = [7,3,4,5,2,1,6,6,5,4]
after = [8,4,5,6,2,3,6,8,6,5]
when = ['before', 'after']
when = [when[j] for j in range(2) for i in range(10)]
data = pd.DataFrame({'when':when, 'score':before+after})
data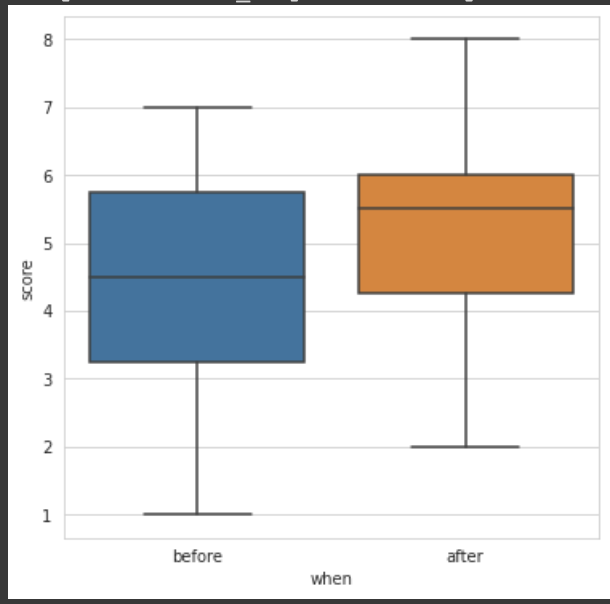

📦 box plot

plt.figure(figsize=(6,6))
sns.boxplot(x='when', y='score', data=data)

그림으로 봤을 때는 처리 후 평균 점수가 올라간 것으로 보인다.

🤓 정규성 검정

#정규성 검정
from scipy.stats import shapiro

normal1 = shapiro(before)
normal2 = shapiro(after)
print(normal1, normal2)

#p-value모두 0.05보다 크기 때문에 정규성에 문제가 없음.

😎 등분산 검정

# 등분산성 고려
from scipy.stats import levene
print(levene(before, after))

from scipy.stats import bartlett
print(bartlett(before, after))

#p-value가 0.05보다 커서 등분산성이 있다고 할 수 있다.

👕 대응표본 t-검정

import scipy.stats

# 대응표본 t검정 수행
scipy.stats.ttest_rel(before,after)

업로드중..

역시 p값이 유의수준 0.05보다 낮으므로 집단 간 유의미한 차이가 있다는 결론을 내릴 수 있다.

참고
https://jae-eun-ai.tistory.com/48#%EC%98%88%EC%8B%9C
데이터 과학을 위한 통계학

hyun

이전 포스트

[통계] 통계적 유의성과 p값

다음 포스트