이자율 기간 구조 모델을 통해서 채권의 파생상품들의 위험중립가격을 산정(risk neutral pricing)할 수 있다. 오늘은 간단하게 zero coupon bond의 가격을 구하는 방법을 알아 보겠다.
이자율 기간구조 모형은 다음과 같다. 기존에 binomial model을 활용 했던 방식 처럼 u,d은 bionmial model을 전개하는데 중요한 팩터이고 q,1-q은 위험중립 가격을 구하는데 중요한 팩터이다.
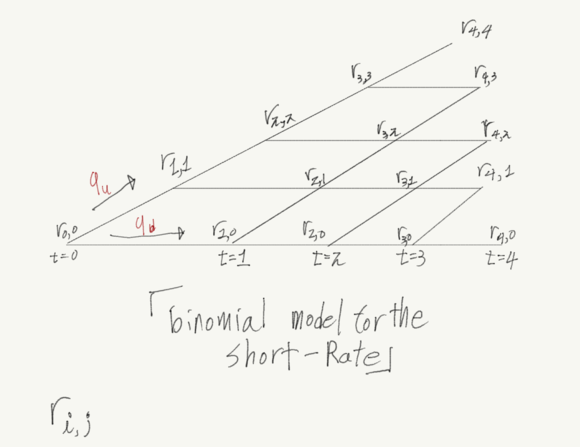
여기서 ri,j는 short-rate를 의미하며 i기와 i+1기 사이의 무위험 이자율이다. 임의의 변수이지만 i기때 r을 알수있다.
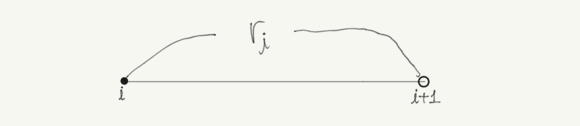
j는 state로써 정확한 번역을 할 수 없었지만 state를 통해서 binomial lattice model에서 격자 위치를 확인 할 수 있다.
간단하게 zero coupon bond(무이표채)의 가격을 구해보자. 무이표채는 고정이자를 지급하지 않고 만기에 액면가를 지불하는 채권이다.
앞으로 무이표채를 나타낼 때 사용할 기호이다.
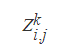
Z:zero coupon bond
k:만기
i:시점
j:state
우리의 최종목표는 가격산정에 있기 때문에 만기가 k기인 무이표채의 현재 시점을 기호로 나타내면
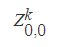
이된다.
무이표채의 가격을 구하는 것 역시 만기 시점에서 현재 시점까지 위험중립가격을 거꾸로 구하게 되면 된다.
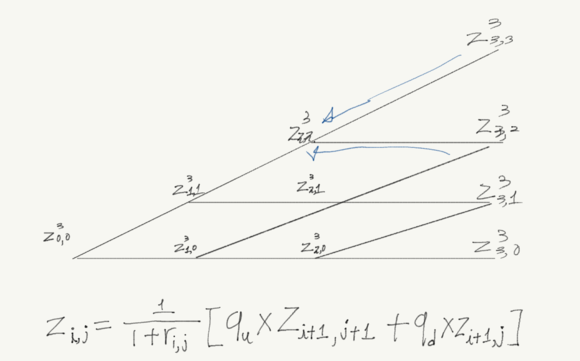
심플하게 아래와 같이 정리할 수도 있다.

예제: 만기가 4기에 액면가가 100인 무이표채의 현재 가격을 구해보자.
우선은 short rate을 구해야한다. 조건은 다음과 같다.

r0,0이 6%일때 short rate lattice는 다음과 같다.
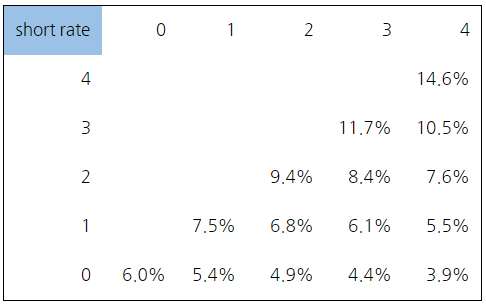
( x축은 기간 i를 나타내며, y축은 state를 나타낸다. )
위 표를 이용하여 다음의 식을 활용하여 무이표채의 가격을 구할 수 있다.
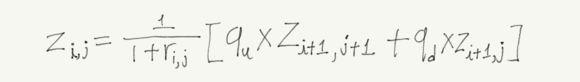
무이표채는 만기에 액면가를 지불하게 되므로 t=4의 현금흐름은 100으로 각 노드 마다 위험중립 가격을 계산해 주면 된다.
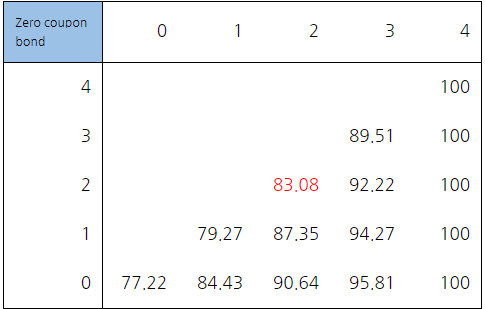
예를 들어 Z2,2의 가치는 다음과 같다.
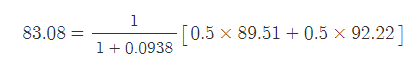
이 과정을 계속 반복하면 현재가치를 구할 수 있다.
