이전 까지 1기간에 벌어진 기초자산가격의 변동을 이항분포로 만들어 위험중립확률의 기댓값으로서 가격산정을 했습니다. 우리가 사용한 로직을 이용한다면, 기간이 길어짐에도 불구하고 똑같은 방법으로 파생상품의 자산을 구할 수 있습니다. 물론 계산은 복잡해 지기 때문에 엑셀을 이용하시면 편리해 집니다.
오늘은 만기가 3년인 옵션의 가격을 구할 것입니다. (다음시간에 선물과 선도 스왑은 기간구조 격자를 통해 구해보도록 합시다.)
우선 기초자산인 주가의 변동을 이항분포 모델로 만들어 봅시다
기초자산은 상승시 u: 1.07 상승하고, 하락시 d: 1/(1.07)
또한 무위험수익률 r:1.01입니다.
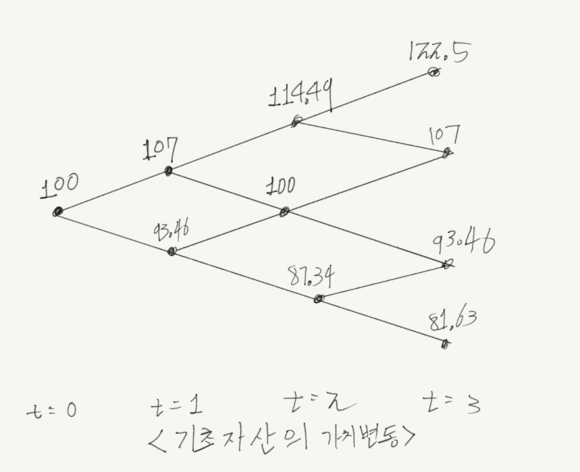
이 주식을 기초자산으로한 유러피안 콜옵션의 만기시 페이오프를 살펴 봅시다.
T=3
k=100
유러피안 콜옵션의 페이오프는 max(s-k,0)입니다.
t=2때 ?노드의 가치를 구하기 위해서 기존에 1기간의 이항분포 모델을 사용해서 구한 것과 같이 위험중립확률을 구한뒤 기댓값을 구해주면 됩니다. 그 결과는 아래 그림과 같습니다.
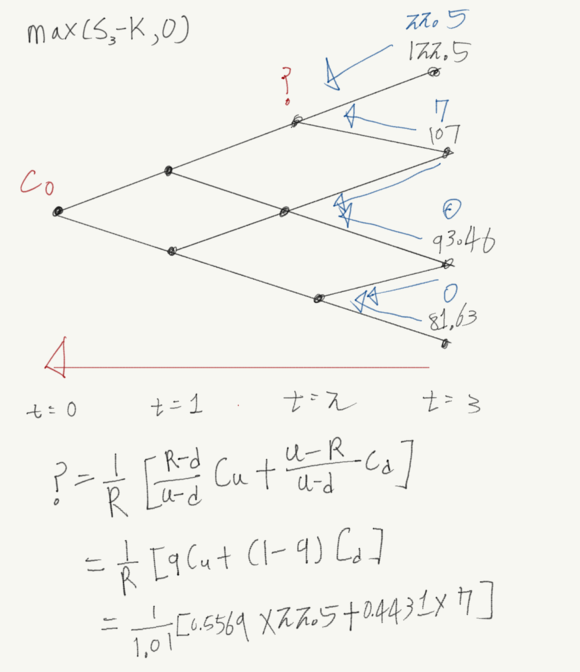
이과정을 backward라고 하는데 계속 반복하면 유러피안 콜옵션의 가치를 구할 수있다.
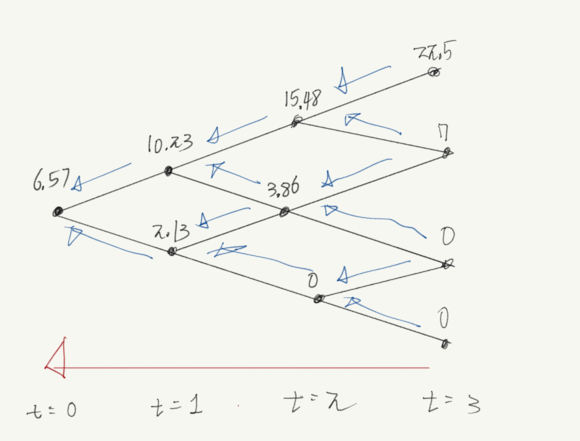
아니면 심플하게 위험중립확률의 조합을 통해 유러피안 옵션의 가치를 구할수 있습니다.
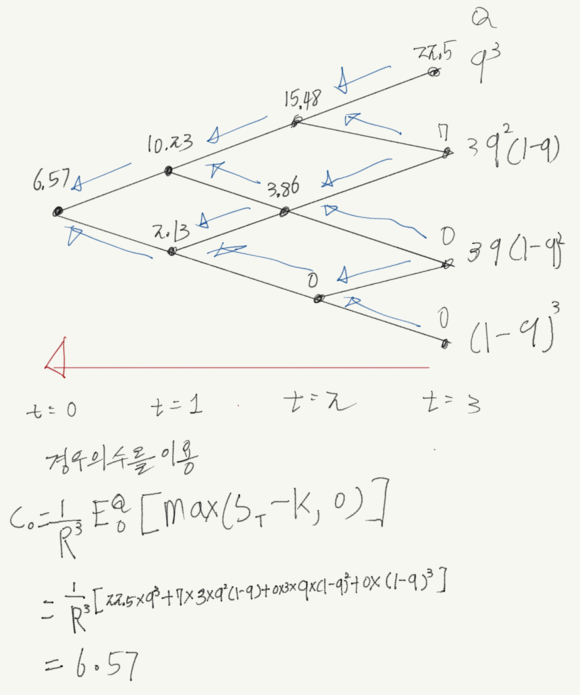
이번에는 조금더 복잡하 아메리칸 풋 옵션의 가치를 구해봅시다
아메리칸 옵션은 만기에만 행사가능한 유러피안 옵션과는 달리 매기 행사가 가능합니다.
아메리칸 풋옵션의 각기의 페이오프는 다음과 같습니다.
max(k-s,0)
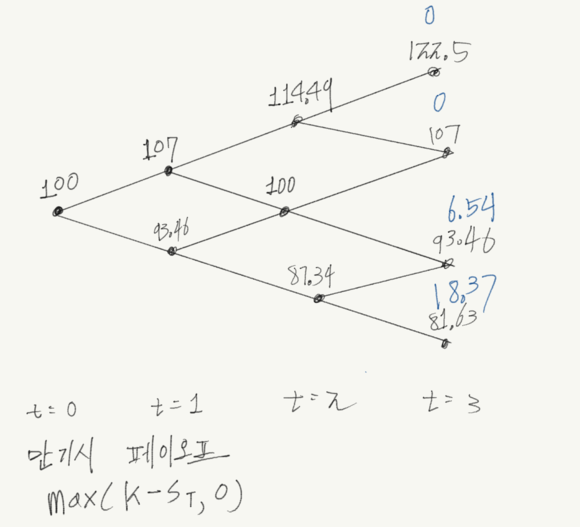
아메리칸 풋옵션의 가격을 구하기 위해서 위험중립확률의 기댓값을 구해야 하지만 행사 여부 또한 계산에 포함되어야 합니다. 행사시 가격과 행사하지 않을때의 기댓값중 더 큰 값이 좋은 선택일 것입니다.
그렇기 때문에 각노드의 값은
max(K-Sn,1/R*EQ[Sn+1]이 되어야 합니다.
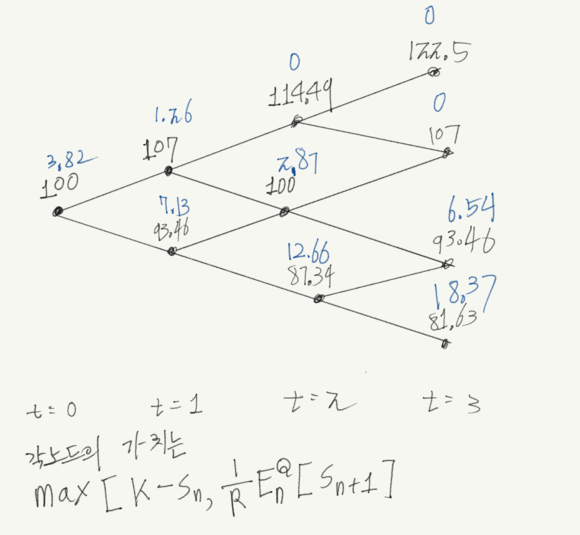
이로써 이항분포(binomial) 모델을 통해 파생상품의 가격을 구해봤습니다. 다음 시간에는 블랙숄즈를 통해서 옵션의 가격을 더 자세히 공부해 보도록 합시다.
