옵션의 정의: 미리 정해진 조건에 따라 일정한 기간 내에 상품이나 유가증권 등의 특정자산을 사거나 팔 수 있는 권리를 말한다.
옵션은 파생상품 4형제(선도, 선물, 스왑, 옵션)중 가장 이질적이고 비선형적인 페이오프를 가지고 있기 때문에 직관적인 이해도 어렵다. 찬찬히 살펴보도록 하자
파생상품의 기초에서도 말했 듯이 contingent claim으로 long포지션은 기초자산을 살 권리를 구매한 것이다.
이전에 살펴 봤던 forward, future, swapt은 모두 만기시 거래를 성사시켜야 하는 의무가 있지만
option에서는 long포지션은 권리를 행사하고 short 포지션만 의무를 가지고 있다. 이렇게 만 말하면 short포지션은 손해만 보는 장사 같지만 option은 다른 파생상품과는 다르게 계약 시점에 long 포지션이 premium을 제공하게 된다.
더알아보기전에 관련 용어를 정리해보자
S: 기초자산, 기초자산을 증권으로 한 옵션을 살펴보자 만기시 S의 가격에 따라 옵션의 payoff가 결정된다.
옵션의 행사: 만기시 long포지션은 권리를 행사 할지 않할지 결정하게 된다. 영어론 exercise라고 한다.
행사가격: K나 X로 주로 표현하는데 옵션 거래 초기 만기에 기초자산을 거래할 가격을 설정하는데 이를 행사가격이라고 한다.
만기일: T라고 표시한다.
무위험이자율: r
콜옵션 vs 풋옵션
콜옵션은 기초자산을 합의된 가격에 매수 할 권리를 거래하는 것이다.
반면에 풋옵션은 기초자산을 합의된 가격에 매도 할 권리를 거래한다.
만기시 long포지션의 payoff와 profit(option premium 지불의 합친 손익) 다음과 같다.
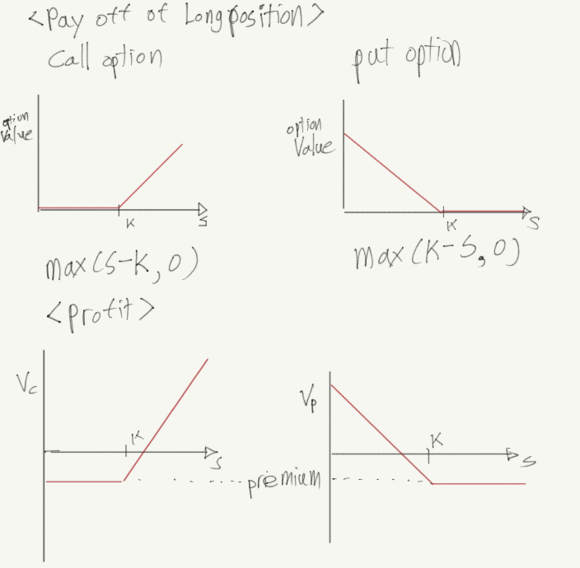
long 포지션은 기초자산을 매수할(call) 혹은 매도할(put) 권리를 산 포지션을 의미한다.
call option는 행사가에 매수할 권리를 구매한 것이므로 max(S-K,0)는 만기시 주가가 행사가격보다 높지 않다면 행사하지 않는 것이고 반대로 행사가격보다 높다면, 그 차액만큼 이익을 보는 것을 의미한다.
short 포지션의 pay off와 profit은 다음과 같다. long 포지션의 거울상과 같은 모습이다.
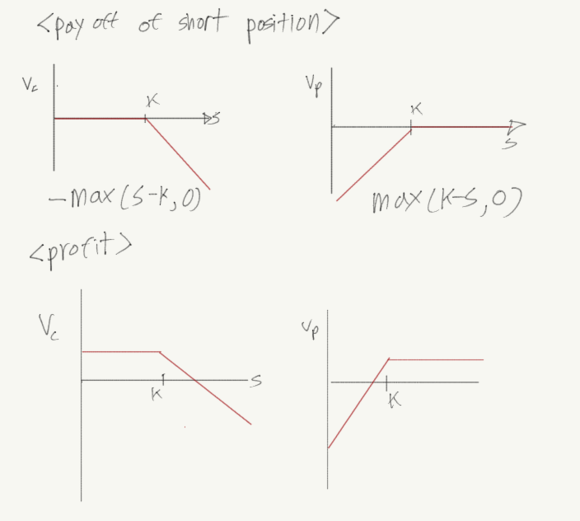
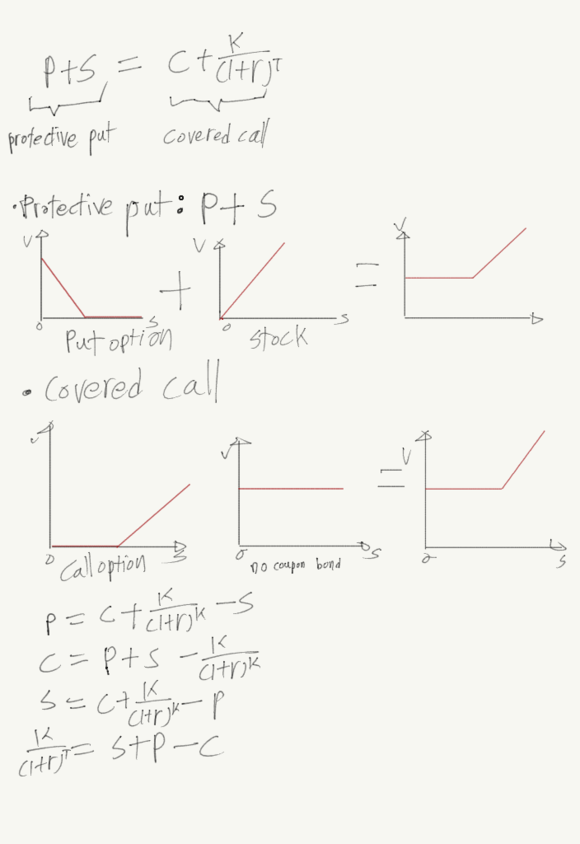
put call parity
풋과 콜 그리고 주식, 무이표채를 payoff를 합성하면 다음과 같은 등식이 성립한다. P+S=C+K/(1+r)^T 또한 이 등식을 활용해 개별 자산의 pricing도 가능해진다.
옵션의 가격 산정
옵션의 가격 산정을 위해 이항모델을 이용해 보자.
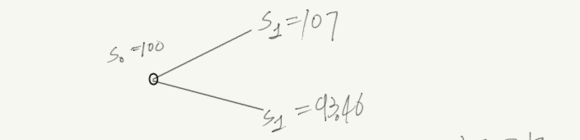
먼저 t=0기의 S0=100인 주식이 있고 t=1에 가격이 S1=107, 93.46인 주식이 있고 이를 기초자산으로하는 k=100인 주식을 call option을 구매했다고 해보자. (r=0.01이다.) 그림은 아래와 같다.
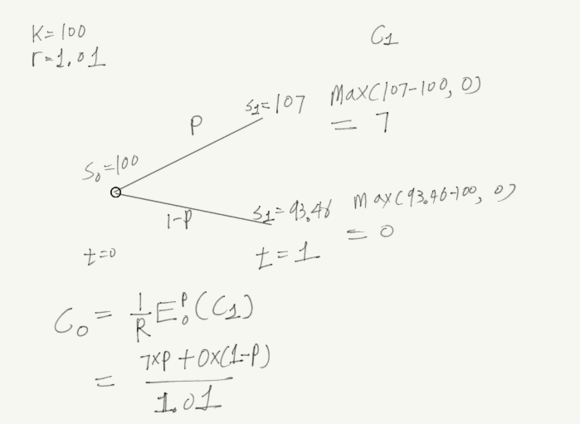
1기의 C1의 가치는 max(S-k,0)이 될 것이고 C0의 가치는 1기 때 payoff의 기대값을 무위험이자율로 할인한 가격이 될것이다.
아래의 그림은 주가가 오를 확률과 주가가 내릴 확률이 다른 주식을 기초자산으로 call option이다. 과연 이들의 가격은 다를까?

결론 부터 말하자면 둘의 가격은 같다.
우리는 위와 같은 payoff를 가져다주는 포트폴리오를 구성하면 옵션의 가격을 구할 수가 있다. 이는 같은 현금흐름을 제공하는 상품의 가격이 같다는 즉 일물일가의 법칙을 이용하는 것이다.
우리는 1기에 주가 변동에 따라 각각 7혹은 0의 현금흐름을 갖는 포트폴리오를 만들 것이다.
첫째로 0기에 주식 S를 x개 만큼 매수하고 1기에 매도할 것이다.
둘째로 0기에 y만큼 대출을 받아 1기에 무위험이자율(r=1.01)의 이자와 같이 상환한다.
포트폴리오 1기의 수익은 다음과 같다.
-주가가 올랐을때:
107x+1.01y=7
-주가가 떨어졌을때:
93.46x+1.01y=0
방정식을 풀면
x=0.517 y=-47.83가 나오게 된다.
(y가 음수인 것은 0기 때 대출을 했기 때문이다.)
그래서 0기때 포트폴리오의 가치는?
C0=S0x+y=100*0.517-48.32=3.86
이 나오게 된다.
위험중립확률
이번에는 위험 중립확률에 대해 배울 것이다. 위험중립확률은 실제 확률이 아닌 페이오프를 기반으로 복제해낸 포트폴리오 비용을 프라이싱한 확률이다. 무위험 수익률 r, 0기와 1기사이의 가격변동인 u(상승시 변동), d(하락시 변동)을 이용해, 위험중립확률 q를 구하고 이를 통해 기대값을 구할 수있다.

옵션의 가치를 구할 때 실제 확률이 아닌 위험중립 확률을 사용하는 이유는 시장을 완전시장으로 가정하기 때문이다. 완전시장에서는 리스크를 헷지 할 수 없다. 그렇기 때문에 같은 현금흐름을 가져다주는 상품의 가격은 같아야 하기 때문이다. 그렇기 때문에 무위험확률을 사용하여 위험중립확률을 구하는 것이다.
