내적을 유한한 요소를 갖는 벡터에 대해서 다루던 기존과 달리 을 n개의 값을 가지는 함수로 생각할 수 있으며, 내적의 개념은 유한한 갯수의 요소를 갖는 벡터와 연속된 값의 함수로 일반화할 수 있다. 그러면 각 벡터요소들의 합은 적분으로 바뀐다.
의 내적은 다음과 같이 정의된다.
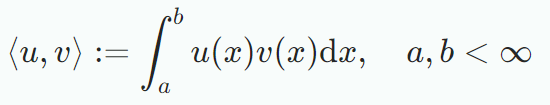
위의 식이 0이라면 두 함수는 직교한다. 유한차원의 벡터에서의 내적과 달리 함수의 내적음 발산하여 무한대값을 가질 수 있다.
내적을 유한한 요소를 갖는 벡터에 대해서 다루던 기존과 달리 을 n개의 값을 가지는 함수로 생각할 수 있으며, 내적의 개념은 유한한 갯수의 요소를 갖는 벡터와 연속된 값의 함수로 일반화할 수 있다. 그러면 각 벡터요소들의 합은 적분으로 바뀐다.
의 내적은 다음과 같이 정의된다.
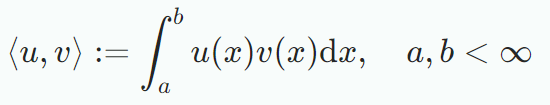
위의 식이 0이라면 두 함수는 직교한다. 유한차원의 벡터에서의 내적과 달리 함수의 내적음 발산하여 무한대값을 가질 수 있다.